В настоящее время для вычисления оценок параметров физических полей предложено большое число алгоритмов, реализующих различные подходы к задаче обработки сигналов установленных на объекте датчиков. В частности, широко используются разнообразные методы интерполяции – от классической лагранжевой до нелинейных, метод наименьших квадратов, максимума правдоподобия и другие [1,2]. Каждый из этих методов имеет свои достоинства и недостатки, обеспечивает различную точность оценок поля в разных режимах работы объекта и так далее. В связи с этим при выборе конкретного метода восстановления физического поля встает задача выбора лучшего метода, а также, возможно, его оперативной адаптации с учетом характера реальных физических процессов, протекающих в объекте управления.
Для решения этих задач в настоящей работе предлагается использовать совокупность поверочных датчиков, а сам подход к их использованию обосновать следующим образом.
Пусть имеется несколько алгоритмов контроля и ставится вопрос о выборе наилучшего из них. Сравнительный анализ можно выполнить различными способами, при этом лучший алгоритм должен обеспечивать возможно меньшее значение дисперсии даваемых им оценок. Сравнение может быть осуществлено либо на математической модели объекта, либо при проведении специальных экспериментов, либо с использованием штатной системы контроля. Понятно, что последний способ обладает рядом преимуществ, поскольку не требует ни разработки детальной математической модели объекта, ни проведения специальных экспериментов на действующем аппарате.
Задачу можно поставить следующим образом. Пусть имеется  датчиков системы контроля, распределенных в пространстве. Часть из них, равная , где , может быть использована в качестве поверочных (поверочным назовем датчик, показания которого не используются в алгоритмах восстановления физического поля). Физически понятно, что существует некоторое оптимальное количество таких датчиков. Действительно, если число поверочных детекторов мало, т. е. , то также будет мала степень достоверности выбора лучшего метода восстановления поля из-за неоднородности, нестационарности его статистических свойств, возможной неработоспособности некоторых датчиков и т. д. С другой стороны, при достаточно большом числе поверочных датчиков существенно снижается точность восстановления поля по самим алгоритмам, так как, как правило, дисперсия оценок возрастает с уменьшением числа датчиков (т. е. с увеличением расстояния между ними). Ухудшение качества оценок поля также уменьшает степень достоверности выбора лучшего алгоритма и может привести к ошибочным выводам.
Таким образом, видимо, существует оптимальное число поверочных датчиков.
Рассмотрим метод выбора оптимального числа поверочных датчиков. Сигнал -го датчика и оценку значения физического поля, полученную в данной точке по -му алгоритму восстановления, соответственно запишем в виде

 (1)

 (2)

где  – истинное значение поля в точке ;  – систематические погрешности датчика и -го алгоритма восстановления для точки ; – случайные погрешности датчика и -го алгоритма восстановления поля в точке .
Обычно предполагают [3-5], что  и  - случайные процессы со следующими статистическими характеристиками

 (3)

Справедливость последнего равенства в определении (3) обусловлена тем, что показания  поверочных датчиков не используются в алгоритмах восстановления поля.
Рассмотрим статистические характеристики невязки . С учетом соотношений (3) имеем

 (4)

 (5)

Выражение (5) справедливо для любого метода восстановления поля. Ранее отмечалось, что при выборе алгоритма восстановления физического поля в качестве основного критерия целесообразно использовать дисперсию даваемых им оценок, причем лучший алгоритм должен обеспечивать меньшее значение дисперсии. Поэтому, анализируя знак и значение разности дисперсий сравниваемых алгоритмов

 (6)

можно сделать однозначный вывод о том, какой алгоритм - или  - обеспечивает получение оценок поля с меньшей дисперсией в точке . Более того, будем предполагать, что в случае восстановления однородных стационарных физических полей для объективного выбора лучшего алгоритма оценивания достаточно одного работоспособного поверочного датчика, установленного в произвольной -ой точке поля [4].
Однако, наибольший практический интерес представляют неоднородные и нестационарные физические поля. Пусть дисперсия неоднородного стационарного поля описывается функцией , где  - радиус-вектор рассматриваемой точки. В общем случае можно ожидать, что дисперсии оценок сравниваемых алгоритмов восстановления  и  также буду являться функциями . Поэтому для объективного анализа качества оценок, полученных по сравниваемым алгоритмам, необходимо иметь значения  по совокупности точек поля . При выборе таких точек в качестве исходной предпосылки принимается предположение о том, что в случае восстановления однородных стационарных физических полей для объективного выбора лучшего алгоритма оценивания достаточно одного работоспособного поверочного датчика. Поэтому рассматриваемое неоднородное физическое поле в настоящей работе предлагается аппроксимировать рядом квазиоднородных участков, в пределах каждого из которых сравнение алгоритмов восстановления выполнять по одному поверочному датчику в соответствии с соотношением (6). При этом функция аппроксимируется кусочно-постоянной функцией , пересекающей  в местах расположения датчиков. Очевидно, что при такой аппроксимации исходная предпосылка принимается с некоторым допущением в каждой из рассматриваемых квизистационарных областей, причем “степень риска” ее правильного применения зависит от степени неоднородности аппроксимируемого поля, числа участков разбиения , расположения поверочных датчиков в пределах каждого участка, т.е. непосредственно связана с решением задачи о наиболее точной аппроксимации функции .
Таким образом, задача выбора оптимального числа поверочных датчиков сводится к нахождению ряда квазиоднородных участков поля, характеризуемых функцией , наиболее точно аппроксимирующей . Поэтому в настоящей работе в качестве критерия объективного применения исходной предпосылки для совокупности  участков поля предлагается использовать интегральный критерий точности аппроксимации вида

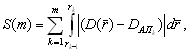 (7)

где  служит для обозначения k-ого участка поля. Очевидно, что можно получить более подробную информацию о качестве оценок того или иного алгоритма восстановления различных участков поля, если стремиться к более точной аппроксимации , и, соответственно, к увеличению числа поверочных датчиков .
Однако ранее отмечалось, что при  существенно снижается точность восстановления поля по самим методикам вследствие потери значительной части измерительной информации.
Будем полагать, что доля потерь полезной измерительной информации для алгоритмов восстановления поля при использовании датчиков в качестве поверочных представима следующим образом:

 (8)

где – общее число установленных датчиков, – дисперсия поля в точке установки -го датчика,  – среднее значение дисперсии по всему полю.
С учетом того, что потерянная для алгоритмов восстановления поля информация с  поверочных датчиков используется для сравнительного анализа самих алгоритмов, функция  в дальнейшем применяется для характеристики относительного увеличения информации при выполнении такого анализа.
Общий же критерий оптимальности выбора количества поверочных датчиков запишем в следующем виде

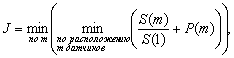 (9)

где .
Заметим, что нахождение минимума функционала  позволяет одновременно оптимизировать не только число поверочных датчиков, но и их месторасположение. Поиск минимума функционала  целесообразно выполнять на ЭВМ, учитывая при этом координаты установленных на объекте датчиков и следующее ограничение:

 (10)

где – расстояние между -м и -м датчиками;  – минимальное допустимое расстояние между поверочными датчиками, при котором максимальное значение дисперсии оценок поля по сравниваемым алгоритмам не превосходит допустимого значения.
Фактически выражение (10) является одним из выводов из рассматриваемой здесь задачи об оптимальном расположении поверочных датчиков – для уменьшения влияния “отключения”  датчиков на качество оценок поля они должны быть как можно дальше разнесены друг от друга в пространстве.
Степень достоверности выбора лучшего алгоритма восстановления поля в дальнейшем может быть обоснована методами теории статистических решений на основе соотношения (6) и знания конкретных законов распределения погрешностей оценок сравниваемых алгоритмов. Кроме того, лучший алгоритм может быть выбран на основе анализа выражения (6) по ряду практических соображений, например, по требованию обеспечения минимальной дисперсии оценки в областях поля со значениями параметров, близкими к предельно допустимым.
Рассмотренный метод выбора оптимального числа поверочных датчиков и лучшего алгоритма восстановления поля применим и в случае нестационарных неоднородных полей. При этом имеющиеся в сигналах датчиков и оценках поля регулярные составляющие должны быть удалены с применением того или иного цифрового фильтра [6], а дальнейший анализ может быть выполнен по приведенной выше схеме. Изложенный метод выбора оптимального числа поверочных датчиков проиллюстрируем на примере при следующих предположениях: дисперсия двумерного физического поля характеризуется осевой симметрией и описывается функцией
,
где м, общее число датчиков  и 0,8 м, датчики системы контроля размещены на равномерной сетке с шагом =0,4 м.
В соответствии с критерием (9) определим число поверочных датчиков, а с учетом условия (10) – один из вариантов их расположения на картограмме. Для удобства функционал (9) запишем в виде

 (11)

где ? и ? – константы
Можно показать, что в случае монотонной функции D(r) поиск минимума функционала  для фиксированного  сводится к решению системы нелинейных алгебраических уравнений вида

, (12)

где  - координаты оптимально расположенных поверочных датчиков.
Численное решение системы (12), обеспечивающее минимум функционала , было получено для . На рис. 1 приведен график зависимости значения  от числа поверочных датчиков . Минимальное значение  достигается при . 

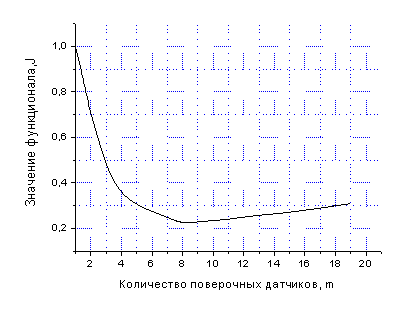
Рис. 1. Зависимость значений функционала от числа поверочных датчиков

Проведенные численные исследования позволили выявить следующие характерные особенности предлагаемого метода:

при выбранном критерии оптимальности в качестве поверочных достаточно использовать небольшую – в пределах 10-15% – часть установленных на объекте датчиков;
расположение поверочных датчиков характеризуется большей плотностью в областях поля с сильно выраженной неоднородностью статистических характеристик.Таким образом, предлагаемый метод выбора оптимального числа поверочных датчиков для проведения сравнительного анализа алгоритмов восстановления физических полей позволяет определить число датчиков и их взаимное расположение. По соотношению (6) можно судить о применимости конкретного алгоритма восстановления.

1. Калиткин Н. Н. Численные методы М.: Наука, 1976.
2. Бахвалов Н. С., Жидков Н. П., Кобельков Г. М.   Численные методы. Москва: БИНОМ;     2004.
3. Сейдж Э., Мелса Дж. Теория оценивания и ее применение в связи и управлении: Пер.с     англ. М.: Связь, 1976.
4. Гандин Л. С., Каган Р. Л. Статистические методы интерпретации метеорологических данных. Л.: Гидрометеоиздат, 1978.
5. Веселов В. В., Гонтов Д. П., Пустыльников Л. П. Вариационный подход к задачам интерполяции физических полей. М.: Наука, 1983.
6. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов: Пер. с англ. М.: Мир, 1978.

Все статьи автора «Саманчук Владимир Никифорович»