Частоты и формы собственных колебаний – важнейшие характеристики сооружения, определяющие его отклик на внешние динамические нагрузки. Методы расчета на ветровые, вибрационные, сейсмические и другие динамические воздействия основываются на предварительном определении частот и форм собственных колебаний рассчитываемого сооружения.
В настоящее время динамические расчеты сооружений, в основном, выполняются с использованием программно-вычислительных комплексов на базе алгоритмов метода конечных элементов (МКЭ). На первом этапе решения данной задачи необходимо сформировать расчетную динамическую модель (РДМ) сооружения (расчетную схему). При использовании МКЭ, как известно, расчетная схема формируется из конечных элементов, соединенных между собой в узлах. В динамических задачах в узлы расчетной схемы вводятся инерционные массы. 
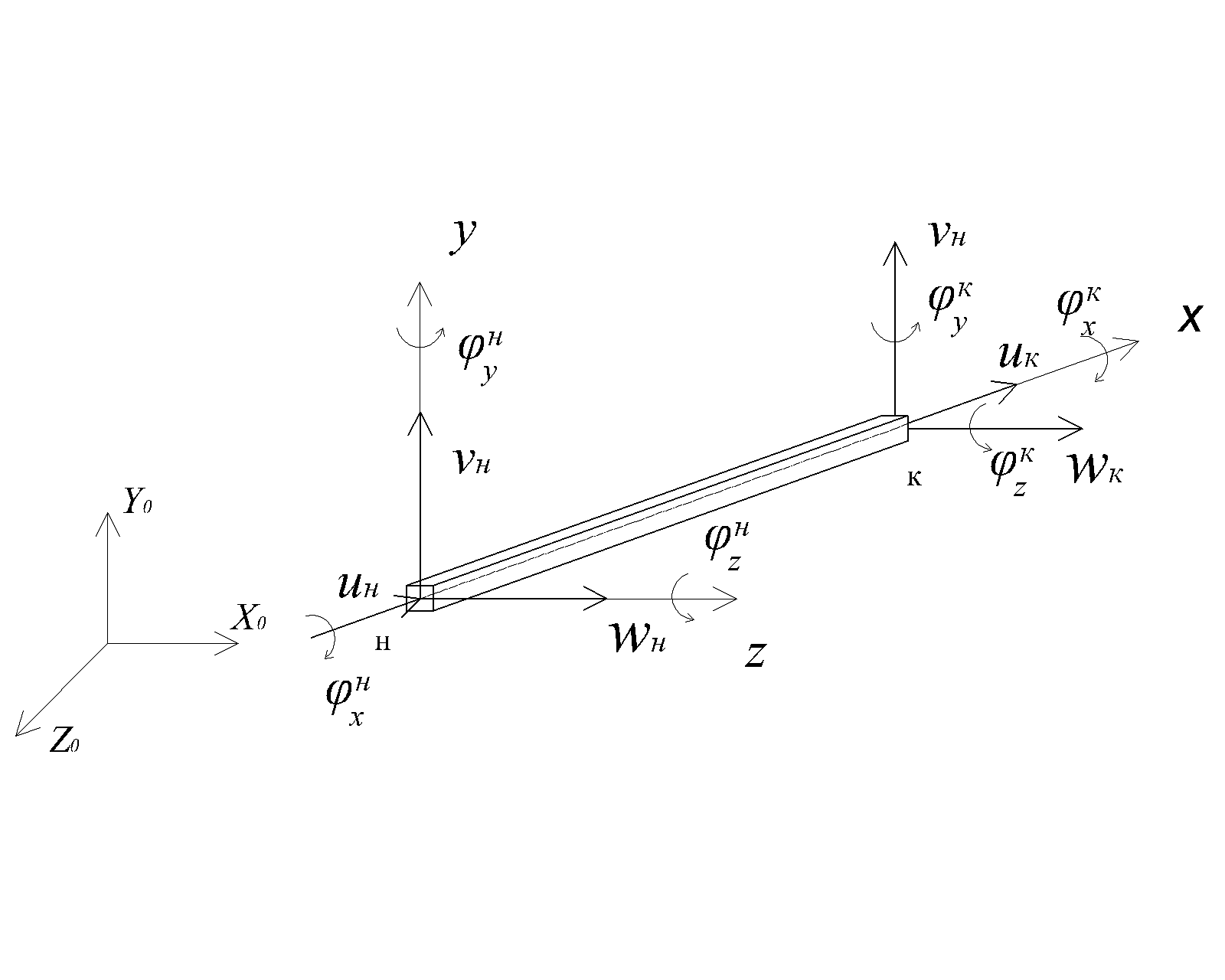
В данной работе используется стержневой пространственный конечный элемент (КЭ) прямоугольного поперечного сечения (рис. 1, а), имеющий 6 степеней свободы в узле.

а)	б)

При этом предполагается, что при совмещении локальной оси x стержня и оси Х0 глобальной системы координат оси y и z локальной системы координат совпадают с осями Y0 и Z0 глобальной системы.
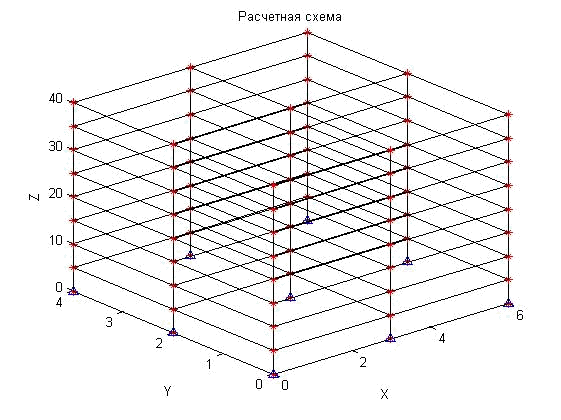
В качестве РДМ принята расчетная схема пространственного каркаса здания, где инерционные массы находятся в местах пересечения стоек и ригелей (рис. 1, б). При этом величина массы в узле определена полусуммой масс стержней, сходящихся в узле.
Матричное уравнение МКЭ в форме перемещений задачи свободных колебаний имеет вид:
 , (1)
где K – матрица жесткости системы в общей системе координат X0 Y0 Z0 ;
М – матрица масс;
Z – вектор амплитудных значений перемещений узлов рассматриваемой системы.
Известно, что система линейных однородных уравнений (1) имеет нетривиальное решение если:
 . (2)
Значения, удовлетворяющие уравнению (2), представляет собой собственные частоты колебаний системы. Умножив выражение (1) на обратную матрицу жесткости  и разделив на , получим:
, или
_, (3)
где  – собственные числа характеристической матрицы , соответствующие собственным частотам колебаний.
Таким образом, задача сводится к определению собственных векторов и собственных чисел характеристической матрицы H, что удобно выполнять при помощи операторов пакета «Matlab».
Разработанное в среде «Matlab» программное средство позволяет:
1. Формировать расчетную схему сооружения (рис. 1, б).
2. Вычислять матрицы жесткости КЭ в локальной системе координат.При этом матрица имеет размерность 12х12, что дает возможность учитывать продольные деформации и кручение стержней.3. Вычислять матрицы масс КЭ.При этом матрица размерностью 12х12 диагональной структуры не имеет на главной диагонали нулевых значений. Элементы матрицы соответствующие деформациям поворотов узлов представляют собой моменты инерции масс конечных размеров относительно соответствующих локальных координатных осей.
4. Формировать глобальные матрицы жесткости и масс конструкции, используя матрицу направляющих косинусов.
5. Решать уравнение собственных значений (3), используя операторы пакета «Matlab» и получить полный спектр частот и форм колебаний конструкции.На рис.2 представлены первые 4 формы колебаний пространственного каркаса, полученные с помощью разработанного программного средства.1-ая форма колебаний = 4.373 рад/с 2-ая форма колебаний = 4.563 рад/с

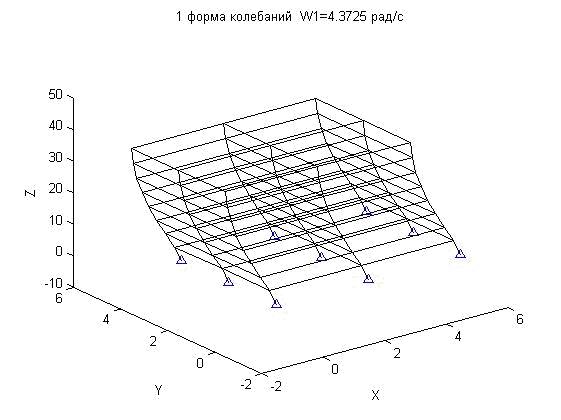
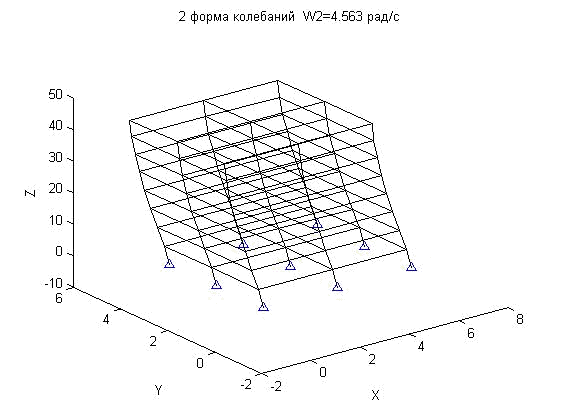
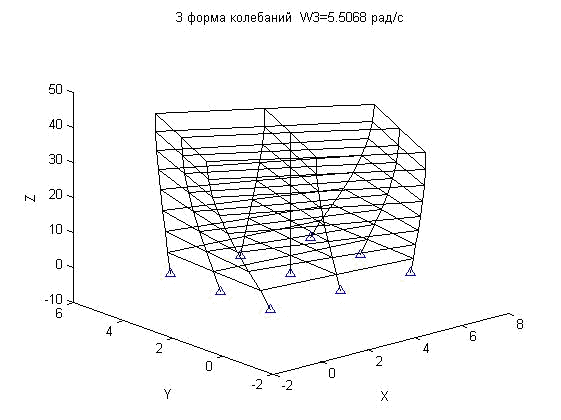
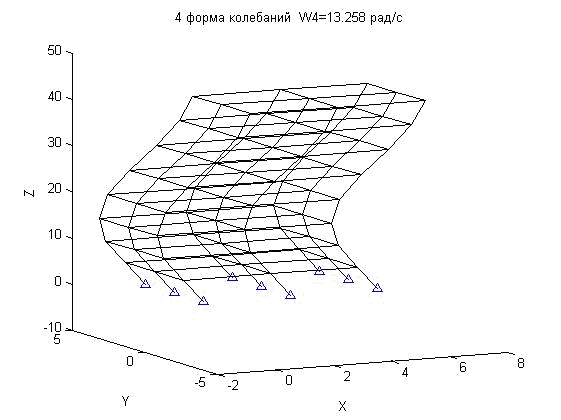
Рис.2.

1. Шеин А.И., Зайцев М.Б. Метод смещенных разностей для решения систем дифференциальных уравнений движения механических систем // Строительная механика и расчет сооружений. 2012. № 2. С. 38-41.

Все статьи автора «Зайцев Михаил Борисович»