Введение
Особенностью атомных электростанций как сложных технических объектов является наличие большого количества элементов оборудования с ограниченным ресурсом работы, начиная от «тяжелого» оборудования, например парогенераторов, насосов, элементов металлоконструкций и кончая периодически заменяемого во время профилактических ремонтов (органы системы управления и защиты (органы СУЗ), разнообразные датчики, топливные сборки и др.). Отметим, что замена отдельных элементов возможна и непосредственно в процессе эксплуатации. Например, в реакторе типа РБМК осуществляется на ходу перегрузка топлива и замена внутриреакторных датчиков энерговыделения. Необходимость замены приборов и оборудования возникает либо по истечению срока службы, либо по причине выхода из строя. И в том и в другом случае необходимо иметь некоторый оперативный запас, чтобы не нарушить режим эксплуатации атомной электростанции – избежать вынужденной остановки. Возникает вопрос об оптимальной величине этого запаса. Дело в том, что излишний запас приводит к «омертвлению, связыванию» средств, а недостаток к возможному нарушению режима эксплуатации вплоть до полной остановки. И в том и в другом случае возникают экономические потери. На выбор оптимальной величины запаса по заменяемому оборудованию и приборам могут повлиять форс-мажорные обстоятельства. (Отметим, что, вообще говоря, проблеме оптимизации запасов на АЭС посвящается немало работ, например [1- 4], вместе с тем, за общностью постановки задач зачастую теряется физический смысл конкретной оптимизационной задачи.)
Ниже приводятся физические постановки и решения двух конкретных задач по оптимизации запасов при возможности форс-мажорных обстоятельств. 
Оптимизация запаса топлива на АЭС с учетом форс-мажорных ситуаций
Современная тенденция развития мировой энергетики такова, что производители топлива и потребители – атомные электростанции (АЭС) – пространственно могут быть разнесены на большие расстояния. Например, атомная электростанция находится в Юго-Восточной Азии, а предприятия по изготовлению топлива в Европе или Северной Америке. Обусловлено это как проблемами нераспространения ядерно-опасных технологий разделения изотопов, так и экономическими и социальными причинами [1]. При этом возможны форс-мажорные обстоятельства, которые нарушают плановый порядок поставки топлива на АЭС: природные катаклизмы, террористические атаки, экономический кризис, различного рода санкции и др. (Отметим, что в настоящее время обсуждаются в различных аспектах вопросы, связанные с оптимизацией работы АЭС при форс-мажорных обстоятельствах [2]). Понятно, что на АЭС необходимо иметь определенный запас свежего топлива. Возникает вопрос: какова должна быть величина этого запаса? Как отмечалось выше, излишний запас приводит к экономическим потерям за счет «омертвления» капитала, а недостаточный запас приводит к вынужденной остановке АЭС и, как следствие, к денежной компенсации потребителю энергии за срыв поставки. 
Рассмотрим простейшую ситуацию, когда АЭС состоит из одного энергоблока.
Обозначим:
- темп выгорания свежего топлива, т.е. количество топлива, выгорающего за единицу времени;
- запас топлива на АЭС;
- время, в течение которого по форс-мажорным причинам не поставляется топливо на АЭС; - случайная величина с плотностью распределения ;
- номинальная мощность реактора;
 и  - коэффициенты, переводящие в денежный эквивалент соответственно, запас топлива и недопоставку электроэнергии.
С учетом введенных обозначений, денежные потери за счет резервирования топлива есть
, а за счет непоставки электроэнергии - . При этом режим работы АЭС такой: если , т.е. запаса топлива хватает на работу, то штрафы не платятся. Если же , то приходится платить штраф. И штраф при этом составляют величину . 
Таким образом, функция потерь есть:

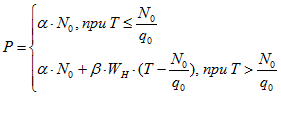
Учитывая, что - случайная величина, имеет смысл говорить о средней потере:

 
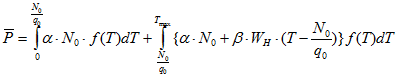
или

с учетом того, что 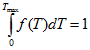, получим:

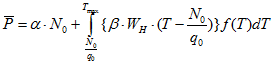
Оптимизационная задача ставится следующим образом: найти какой запас топлива необходимо иметь на АЭС, чтобы в среднем потери при форс-мажорных обстоятельствах были минимальны.
Математическая постановка задачи такова:
Найти ,  (1)
Рассмотрим решение задачи, если - есть плотность распределения случайной величины для закона равномерной плотности на интервале , то есть  
Тогда минимизируемая функция есть:
 ,  (2) 
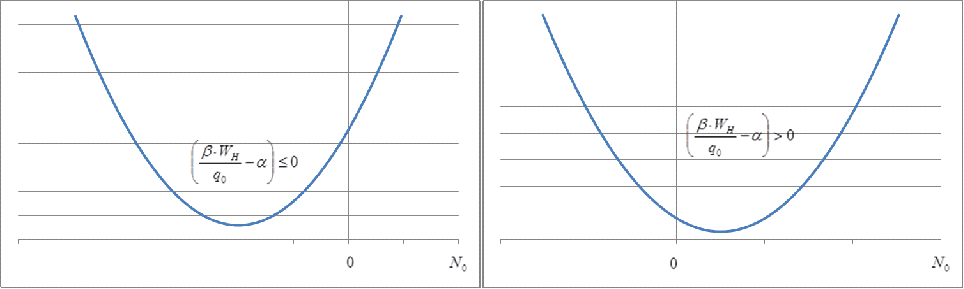
На рисунке 1 показана зависимость средней потери от количества зарезервированного топлива. 

Из рисунка видно:
1. при 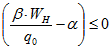 резервировать запас топлива не следует () и . Физически это означает, что «омертвление» средств не окупается компенсацией потребителю в случае недопоставки энергии.2. при  следует резервировать топливо в количестве

 (3)

При этом средняя потеря составит величину:
 (4)Оптимизация запаса датчиков внутриреакторного контроля
Контроль за распределением энерговыделения в современных мощных ядерных энергоблоках ведется на основе показаний датчиков внутриреакторного контроля [1]. В процессе работы часть датчиков может выходить из строя, что приводит к необходимости их замены. Если по каким- либо причинам это невозможно, например, из-за их отсутствия, то точность контроля за полем энерговыделения снижается, поскольку снижается число точек контроля. Это приводит к необходимости снижать общую мощность реактора, чтобы избежать превышения лимитирующих параметров, например, таких как линейная нагрузка.
Предположим, что мощность реактора связана с числом датчиков энерговыделения в ядерном реакторе линейной зависимостью: 
,
где - номинальное число датчиков контроля;
- число датчиков контроля в момент времени ;
- коэффициент связи.
Пусть, в свою очередь, число требующих замены датчиков контроля линейно зависит от времени: 
Если  таково, что дефицит средств контроля может быть восполнен за счет запасов, то мощность энергоблока не снижается. Как только запас исчерпан, то мощность снижается до величины . И потребителю не отпускается мощность 
То есть если мощность не снижается. Таким образом, Мощность снижается, если .
Потери составляют величину:

Учитывая, что – случайная величина, имеет смысл говорить о средней потере:

Математическая постановка оптимизационной задачи такова:
Найти ,  
Для закона равномерной плотности получим :
 
Анализ выражения показывает следующее:1. при резервировать запас датчиков не следует () и . Физически это означает, что «омертвление» средств не окупается компенсацией потребителю в случае недопоставки энергии.
2. при следует резервировать количество датчиков . И средняя потеря будет .
Таким образом, существует возможность уменьшения экономических потерь при форс-мажорных обстоятельствах за счет оптимального резервирования запасов на АЭС.

1. Ядерная энергетика. Проблемы. Решения / Под ред. М.Н. Стриханова.- В 2 частях.- Часть 1. – М.: ЦСПиМ, 2011. – 424с. : ил.
2. Загребаев А.М., Овсянникова Н.В., Садчиков С.М., Черняев В.В. Средняя потеря энерговыработки при случайной остановке реактора с ограниченным оперативным запасом реактивности. Естественные и технические науки, №2(58), 2012,с.418-422
3. Портнов А.С. «Оптимизация системы логистики атомных электростанций» доклад на конференции «Безопасность, эффективность и экономика атомной энергетики». 21-23 мая 2014 года
4. Лукинский В. С., Лукинский В. В., Чепурин А. К вопросу о совершенствовании алгоритма управления запасами в цепях поставок // Логистика и управление цепями поставок. 2013. No 1(54). С. 12-20.
5. Лукинский В.В. Актуальные проблемы формирования теории управления запасами. СПб.: СПбГИЭУ, 2008. – 213 с.
6. Тюкаев Д.А. Особенности бизнес-планирования в ядерной энергетике // Вестник Российской академии естественных наук. 2011. No4. С.26-28.

Все статьи автора «Садчиков Сергей Михайлович»