Рассмотрим эргатическую систему (рис.1), описываемую с учетом запаздывания как оператора, так и органов управления, уравнениями вида [1…3]:
|
|
(1)
|
где ![]() и
и ![]() - заданные матрицы,
- заданные матрицы, ![]() - векторы соответственно программного движения, отклонения органов управления, отклонения рулей, выходных координат;
- векторы соответственно программного движения, отклонения органов управления, отклонения рулей, выходных координат; ![]() ,
,![]() - постоянные запаздывания (причины запаздывания могут быть различными; лишь предполагается независимость вида последних двух уравнений при использовании для управления различных (по виду и количеству) источников информации). Естественно предположить, что динамика имитатора описывается системой такого же вида, как и (1).
- постоянные запаздывания (причины запаздывания могут быть различными; лишь предполагается независимость вида последних двух уравнений при использовании для управления различных (по виду и количеству) источников информации). Естественно предположить, что динамика имитатора описывается системой такого же вида, как и (1).
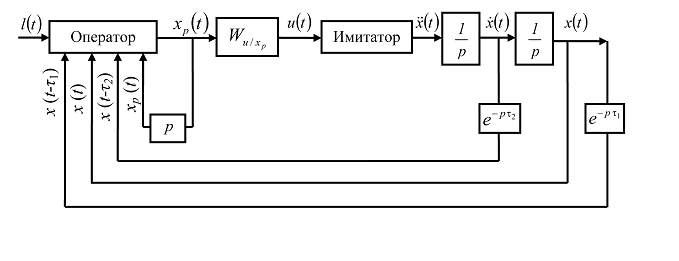
Рис.1. Структурная схема системы
Для оценки стиля управления воспользуемся обобщенным вектором ![]() , компонентами которого являются неслучайные числовые характеристики случайной функции
, компонентами которого являются неслучайные числовые характеристики случайной функции ![]() и элементы матриц
и элементы матриц ![]() . В качестве числовых характеристик используются резонансные частоты
. В качестве числовых характеристик используются резонансные частоты ![]() спектральной плотности
спектральной плотности ![]() , вероятности попадания частоты
, вероятности попадания частоты ![]() в некоторые окрестности точек
в некоторые окрестности точек ![]() ; дисперсии, приходящиеся в эти окрестности; средние амплитуды и длительности импульсов в управляющих воздействиях (легко определяются по данным нормальной эксплуатации [4…7]). Определение элементов
; дисперсии, приходящиеся в эти окрестности; средние амплитуды и длительности импульсов в управляющих воздействиях (легко определяются по данным нормальной эксплуатации [4…7]). Определение элементов ![]() требует наряду с решением задачи идентификации, проведения оценки чувствительности динамических характеристик системы (1) к ошибкам идентификации. Примем
требует наряду с решением задачи идентификации, проведения оценки чувствительности динамических характеристик системы (1) к ошибкам идентификации. Примем ![]() ,
, ![]() и воспользуемся регрессионным методом идентификации (по синхронным измерениям
и воспользуемся регрессионным методом идентификации (по синхронным измерениям ![]() ,
, ![]() ,
, ![]() в процессе нормальной эксплуатации).
в процессе нормальной эксплуатации).
Приведем (1) к виду
|
|
(2)
|
где ![]() ,
, ![]() - n-мерный вектор состояния и m-мерный вектор управления (вход) соответственно; , - матрицы коэффициентов; (
- n-мерный вектор состояния и m-мерный вектор управления (вход) соответственно; , - матрицы коэффициентов; (![]() ). Введем
). Введем
получим
Из (2) будем иметь
|
|
(3)
|
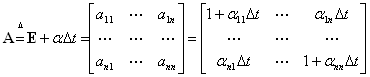 ;
;.gif) .
.Откуда следует
|
|
(4)
|
![]() ,
, .gif) .
.
В силу стационарности матрицы Ф выражение (4) справедливо при всех k. Уравнение (4)эквивалентно системе:
|
x1k+1 = a11 x1k + … + a1 n xnk + b11 u1k + … + b1 m umk ;
x2k+1 = a21 x1k + … + a2 n xnk + b21 u1k + … + b2 m umk ; … xnk+1 = an1 x1k + … + an n xnk + bn1 u1k + … + bn m umk ;
|
(5)
|
(x1k+1, … , xnk+1 определяются изолированно).
Регрессионная идентификация параметров управления
требует знания r n + m + 1 совокупностей синхронных измерений xik+1 и x1k , … , xnk , u1k , … , umk :
…
Справедливо
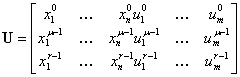 ;
;Откуда для оценки параметров ![]() получим соотношение
получим соотношение
Откуда
.gif) .
.Указанная схема легко может использоваться для идентификации и систем вида (1). В дискретной форме (1) представится в виде
|
|
(
|
![]() - входы,
- входы, ![]() - выход. Если по данным нормальной эксплуатации по указанной выше схеме определить
- выход. Если по данным нормальной эксплуатации по указанной выше схеме определить ![]() , то легко определятся и
, то легко определятся и ![]() .
.
С использованием этой методики осуществлялась параметрическая идентификация эргатической системы с уравнениями движений
|
|
(6)
|
(![]() -синхронные измерения). Обобщенный вектор управления принимался в виде
-синхронные измерения). Обобщенный вектор управления принимался в виде
|
|
(7)
|
![]() определялись в соответствии с [3];
определялись в соответствии с [3]; ![]() - средние амплитуды и длительности импульсов управляющих воздействий.
- средние амплитуды и длительности импульсов управляющих воздействий.
Справедливо
Ξ=
Ξ=
.gif) ,
,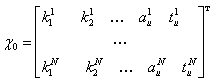 ,
, .gif)
(используются центрированные значения для ![]() систем).
систем).
Все тринадцать компонент вектора ![]() линейно зависят от четырех технических параметров
линейно зависят от четырех технических параметров ![]() ,
,![]() в рассматриваемых интервалах их изменения.
в рассматриваемых интервалах их изменения.
Библиографический список
- Авиационные тренажеры модульной архитектуры: монография; под редакцией Лапшина Э.В., д.т.н., проф. Данилова А.М. – Пенза: ИИЦ ПГУ. – 2005. – 146 с.
- Гарькина И.А., Данилов А.М., Домке Э.Р. Математическое моделирование управляющих воздействий оператора в эргатической системе / Вестник Московского автомобильно-дорожного государственного технического университета (МАДИ). –2011. – № 2. – С. 18-23.
- Гарькина И.А, Данилов А.М., Пылайкин С.А. Транспортные эргатические системы: информационные модели и управление / Мир транспорта и технологических машин. – №1(40). – 2013. – С.115-122.
- Гарькина И.А., Данилов А.М., Пылайкин С.А.Тренажеры и имитаторы транспортных систем: выбор параметров вычислений, оценка качества / Мир транспорта и технологических машин. – 2013. – № 3 (42). – С. 115-120.
- Данилов А.М., Домке Э.Р., Гарькина И.А. Формализация оценки оператором характеристик объекта управления / Известия ОрелГТУ. Информационные системы и технологии. – 2012. – № 2 (70). – С.5-11.
- Будылина Е.А., Гарькина И.А., Данилов А.М. Приближенные методы декомпозиции при настройке имитаторов динамических систем / Региональная архитектура и строительство. – 2013. – № 3. – С. 150-156.
- Гарькина И.А., Данилов А.М., Петренко В.О. Решение приближенных уравнений: декомпозиция пространственного движения управляемого объекта // Современные проблемы науки и образования. – 2014. – № 5; URL: http://www.science-education.ru/119-14766.
