В настоящее время считается, что тепловая или гравитационная конвекция в земном ядре является причиной, которая приводит к созданию геомагнитного поля [1,2]. Теория геомагнитного поля получила название гидромагнитного динамо (ГД) по аналогии с действием обычной динамо-машины с самовозбуждением. Математическая трактовка теории вихревого движения в ядре и возникновения в нем индукционных токов сложна и в общем виде до сих пор не получила своего решения [1], так как решение уравнений магнитной гидродинамики сопряжено с большими трудностями. Поэтому теория ГД еще использует кинематические модели, в которых скорость жидкости считается заданной, а определяется тепловое и магнитное поле [3]. Согласно этой концепции такой подход можно сравнить с электродинамикой слабых полей, которая не учитывает влияния электромагнитных полей на движение жидкости [3]. В этой связи исследование гидродинамики жидкого ядра Земли представляет самостоятельный интерес, который в дальнейшем позволит оценить влияние магнитного поля на гидродинамику при решении уравнений магнитной гидродинамики и теплообмена.
В настоящей работе рассматриваются полные уравнения магнитной гидродинамики: энергии, с учетом внутренних источников тепла, равномерно распределенных в жидкости [3], и джоулевой диссипации; движения, с учетом магнитных, инерционных, вязких и подъемных сил; магнитной индукции; неразрывности для скорости и магнитной индукции. Используется приближение Буссинеска. Ускорение свободного падения направлено к центру сферического слоя. Рассматривается стационарный режим.
Математическая постановка задачи в переменных вихрьфункция токатемпература в безразмерной форме в сферической системе координат с учетом симметрии по долготе имеет вид [4]:
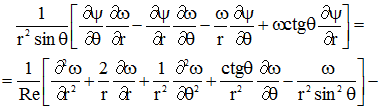
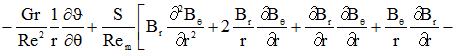 (1)
(1).gif)
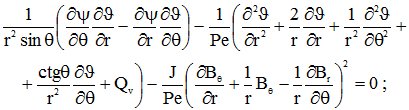 (3)
(3)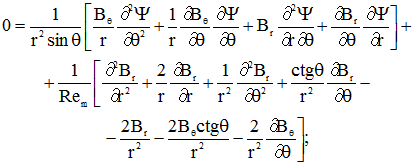 (4)
(4)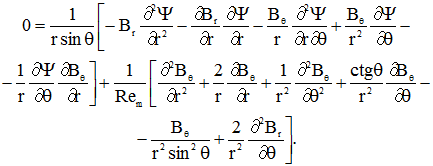 (5)
(5)При записи системы дифференциальных уравнений (1)-(5) использованы следующие обозначения: ![]() ,
,![]() безразмерные температура, магнитная индукция, функция тока и напряженность вихря;
безразмерные температура, магнитная индукция, функция тока и напряженность вихря; ![]() характерные масштабы;
характерные масштабы; .gif) безразмерный внутренний источник теплоты;
безразмерный внутренний источник теплоты; ![]() размерный внутренний источник теплоты;
размерный внутренний источник теплоты; ![]() размерный тепловой поток тепла, отводящийся от внешней поверхности слоя;
размерный тепловой поток тепла, отводящийся от внешней поверхности слоя; ![]() безразмерный текущий радиус;
безразмерный текущий радиус; ![]() размерный текущий радиус;
размерный текущий радиус; ![]() размерные радиусы внутренней и внешней сферы;
размерные радиусы внутренней и внешней сферы; ![]() полярный угол;
полярный угол; ![]() коэффициент магнитной вязкости;
коэффициент магнитной вязкости; ![]() электрическая проводимость жидкости;
электрическая проводимость жидкости; ![]() безразмерная толщина сферического слоя;
безразмерная толщина сферического слоя; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, .gif) безразмерные числа Грасгофа, Рейнольдса, Пекле, магнитное число Рейнольдса, параметр магнитного взаимодействия. Остальные обозначения общепринятые. Постоянная величина J, входящая в уравнение энергии (3), определяет величину джоулевой диссипации.
безразмерные числа Грасгофа, Рейнольдса, Пекле, магнитное число Рейнольдса, параметр магнитного взаимодействия. Остальные обозначения общепринятые. Постоянная величина J, входящая в уравнение энергии (3), определяет величину джоулевой диссипации.
В работе при проведении вычислительного эксперимента для температуры задавались следующие граничные условия: на внутренней поверхности слоя ![]() (
(![]() ) граничное условие первого рода (постоянное значение температуры), а на внешней поверхности
) граничное условие первого рода (постоянное значение температуры), а на внешней поверхности ![]() (
(![]() ) граничное условие второго рода (отвод тепла) [2]:
) граничное условие второго рода (отвод тепла) [2]: ![]()
.gif) . Для заданных граничных условий постоянная величина
. Для заданных граничных условий постоянная величина ![]() вычислялась по формуле:
вычислялась по формуле: .gif) .
.
Граничное условие для температуры на оси симметрии: .gif) .
.
Граничные условия для функции тока, напряженности вихря и магнитной индукции имели следующий вид:
.gif) ;
;Граничные условия для вихря на границах сферического слоя предполагают линейное изменение его по нормали [5].
Локальные числа Нуссельта на границе внутренней и наружной сферы рассчитывались по формулам:
.gif)
Осредненные числа Нуссельта вычислялись из соотношений:
.gif)
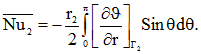
Численное решение задачи осуществлялось с помощью метода конечных элементов. Для аппроксимации рассчитываемых функций использовались билинейные девятиточечные конечные элементы. Система полученных нелинейных алгебраических уравнений решалась методом итераций с использованием нижней релаксации. В качестве начальных приближений задавались нулевые значения напряженности вихря, температуры, функции тока, радиальной и меридиональной составляющих магнитной индукции. Решение считалось достигшим нужной точности, если на текущей итерации для всех расчетных полей модуль разности между новым и старым значением поля в каждом узле становился меньше заданной погрешности. При расчете на каждой «внешней» итерации новых значений температуры, вихря и магнитной индукции, для расчета функции тока из разностного аналога уравнения Пуассона (2) осуществлялся «внутренний» итерационный цикл до достижения заданной степени точности.
В результате численного решения задачи были получены поля температуры, функции тока, напряженности вихря, магнитной индукции и распределения чисел Нуссельта в сферическом слое.
На рисунках 16 приведены результаты расчетов полей температуры, функции тока, напряженности вихря, радиальной и меридиональной составляющих магнитной индукции и распределения чисел Нуссельта. Расчеты проводились для следующих значений безразмерных критериев подобия:
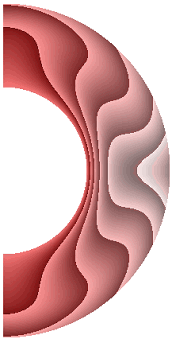
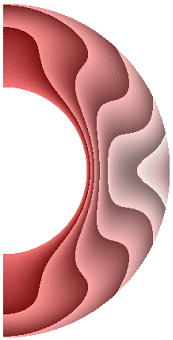
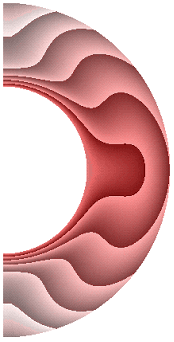
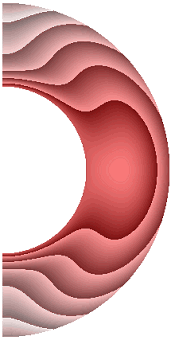
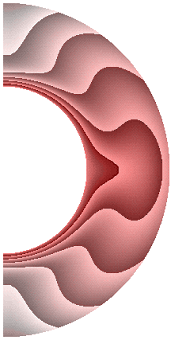
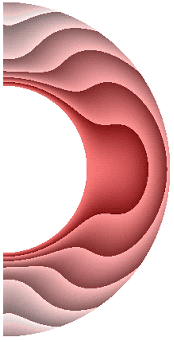
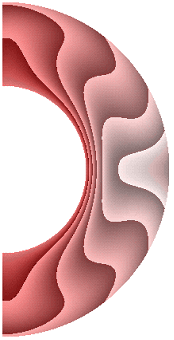
На рисунке 1 приведены результаты расчетов поля температуры.
а б в г д е ж
Рисунок 1 – Поле температуры: а без учета магнитных сил, ![]() б с учетом магнитных сил,
б с учетом магнитных сил, ![]() в с учетом магнитных сил,
в с учетом магнитных сил, ![]() г с учетом магнитных сил,
г с учетом магнитных сил, ![]() д с учетом магнитных сил,
д с учетом магнитных сил, ![]() е с учетом магнитных сил,
е с учетом магнитных сил, ![]() ж с учетом магнитных сил,
ж с учетом магнитных сил, ![]()
Для всех режимов теплообмен в слое осуществляется конвекцией. Диапазон изменения температуры для результата рис. 1, а (13,840; 1). Такая же качественная и количественная ситуация сохраняется и для электропроводной жидкости (рис. 1, б). Учет джоулевой диссипации (рис. 1, в) изменяет поле температуры, особенно в экваториальной области. Диапазон изменения температуры (14,620; 1). Учет внутренних источников и стоков тепла, совместно с учетом джоулевой диссипацией (рис. 1, г, д), приводит к дальнейшему изменению поля температуры. Диапазон изменения температуры для результата рис. 1, г (9,240; 1,537), а для результата рис. 1, д (19,367; 1). Неучет джоулевой диссипации, несмотря на наличие внутренних источников (стоков) тепла (рис. 1, е, ж), изменяет поле температуры. Диапазон изменения температуры для результата рис. 1, е (11,367; 1), а для результата рис. 1, ж (17,981; 1).
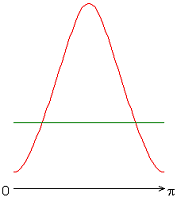
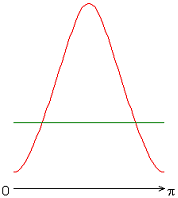
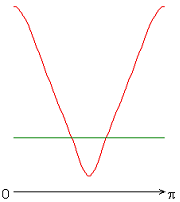
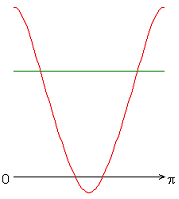
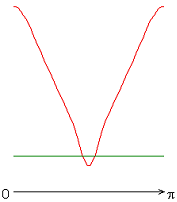
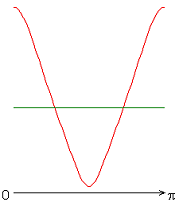
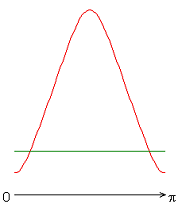
На рисунке 2 приведены результаты расчетов локальных чисел Нуссельта на внутренней (красная линия) и внешней (зеленая линия) поверхности сферического слоя.
а б в г
д е ж
Рисунок 2 – Распределение локальных чисел Нуссельта: а без учета магнитных сил, ![]() б с учетом магнитных сил,
б с учетом магнитных сил, ![]() в с учетом магнитных сил,
в с учетом магнитных сил, ![]() г с учетом магнитных сил,
г с учетом магнитных сил, ![]() д с учетом магнитных сил,
д с учетом магнитных сил, ![]() е с учетом магнитных сил,
е с учетом магнитных сил, ![]() ж с учетом магнитных сил,
ж с учетом магнитных сил, ![]()
Следует отметить, что согласно заданному граничному условию для температуры на внешней границе слоя, распределение локальных чисел Нуссельта совпадает с осредненным и принимает постоянное значение ![]() 20 (здесь и далее). Распределения локальных чисел Нуссельта на внутренней границе слоя имеют или максимум (рис. 2, а, б, ж), или минимум (рис. 2, в-е) при значении полярного угла
20 (здесь и далее). Распределения локальных чисел Нуссельта на внутренней границе слоя имеют или максимум (рис. 2, а, б, ж), или минимум (рис. 2, в-е) при значении полярного угла ![]() (экваториальная плоскость). Значение осредненного и диапазон изменения локальных чисел Нуссельта следующие:
(экваториальная плоскость). Значение осредненного и диапазон изменения локальных чисел Нуссельта следующие:
![]() 37,599; 4,962
37,599; 4,962![]() 56,363;
56,363; ![]() 37,599; 4,962
37,599; 4,962![]() 56,363;
56,363;
![]() 29,411; 5,929
29,411; 5,929![]() 68,228;
68,228; ![]() 8,028; 3,050
8,028; 3,050![]() 32,086;
32,086;
![]() 50,794; 14,493
50,794; 14,493![]() 102,570;
102,570; ![]() 16,198; 1,519
16,198; 1,519![]() 43,750;
43,750;
![]() 59,001; 9,957
59,001; 9,957![]() 84,268 соответственно для результатов рис. 2, а-ж.
84,268 соответственно для результатов рис. 2, а-ж.
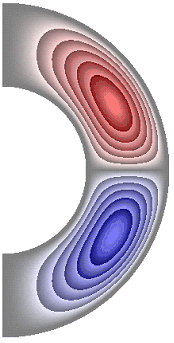
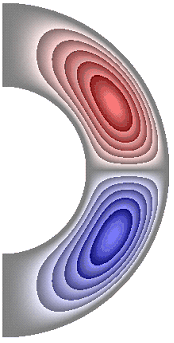
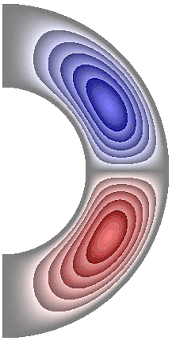
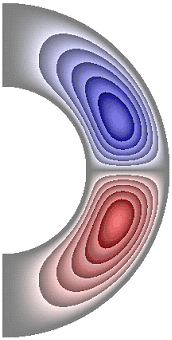
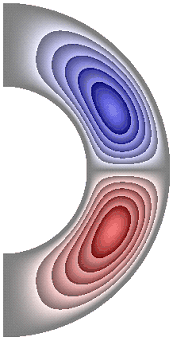
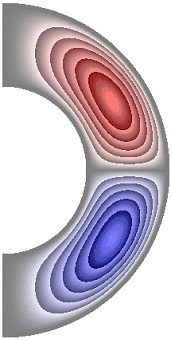
На рисунке 3 приведены результаты расчетов поля функции тока. Для всех случаев в слое образуются две конвективные ячейки. Для результатов, представленных на рис. 3, а, б, ж, жидкость в северном полушарии слоя движется против часовой стрелки (красный цвет значения функции тока положительные), а в южном – по часовой стрелке (синий цвет значения отрицательные). Максимальное значение функции тока соответственно ![]() 5,65; 5,65; 6,77. Учет джоулевой диссипации (рис. 3, в), так же как и учет внутренних источников и стоков тепла, совместно с учетом джоулевой диссипации (рис. 3, г, д), изменяет направление циркуляции жидкости в ячейках на противоположное. Максимальное значение функции тока для результатов рис. 3, в-д
5,65; 5,65; 6,77. Учет джоулевой диссипации (рис. 3, в), так же как и учет внутренних источников и стоков тепла, совместно с учетом джоулевой диссипации (рис. 3, г, д), изменяет направление циркуляции жидкости в ячейках на противоположное. Максимальное значение функции тока для результатов рис. 3, в-д ![]() 5,32; 3,66; 6,62. Неучет джоулевой диссипации, при учете внутренних источников тепла (рис. 3, е), сохраняет направление циркуляции жидкости, а учет внутренних стоков тепла (рис. 3, ж) изменяет направление циркуляции жидкости на противоположное, по сравнению с результатами рис. 3, в-е.
5,32; 3,66; 6,62. Неучет джоулевой диссипации, при учете внутренних источников тепла (рис. 3, е), сохраняет направление циркуляции жидкости, а учет внутренних стоков тепла (рис. 3, ж) изменяет направление циркуляции жидкости на противоположное, по сравнению с результатами рис. 3, в-е.

а б в г д е ж
Рисунок 3 – Поле функции тока: а без учета магнитных сил, ![]() б с учетом магнитных сил,
б с учетом магнитных сил, ![]() в с учетом магнитных сил,
в с учетом магнитных сил, ![]() г с учетом магнитных сил,
г с учетом магнитных сил, ![]() д с учетом магнитных сил,
д с учетом магнитных сил, ![]() е с учетом магнитных сил,
е с учетом магнитных сил, ![]() ж с учетом магнитных сил,
ж с учетом магнитных сил, ![]()
Максимальное значение функции тока для результата рис. 3, е ![]() 4,13.
4,13.
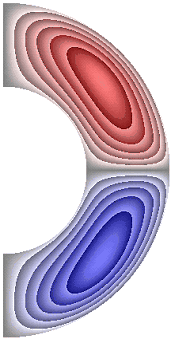
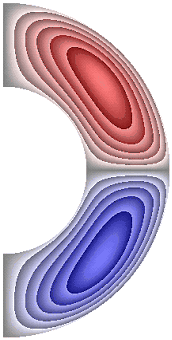
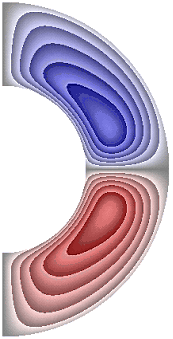
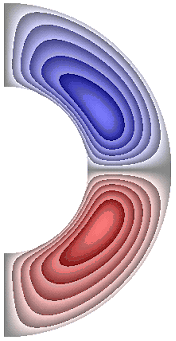
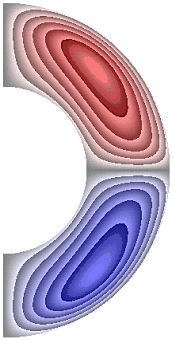
На рисунке 4 приведены результаты расчетов поля напряженности вихря. В слое (рис. 4) образуются два крупномасштабных вихря.


а б в г д е ж
Рисунок 4 – Поле напряженности вихря: а без учета магнитных сил, ![]() б с учетом магнитных сил,
б с учетом магнитных сил, ![]() в с учетом магнитных сил,
в с учетом магнитных сил, ![]() г с учетом магнитных сил,
г с учетом магнитных сил, ![]() д с учетом магнитных сил,
д с учетом магнитных сил, ![]() е с учетом магнитных сил,
е с учетом магнитных сил, ![]() ж с учетом магнитных сил,
ж с учетом магнитных сил, ![]()
В зависимости от режима структура вихрей, хотя и незначительно, но изменяется. Для результатов рис. 4, а, б, ж в северном полушарии жидкость движется против часовой стрелки (значения напряженности вихря положительные), а в южном – по часовой стрелке (значения отрицательные). Максимальная интенсивность вихрей ![]() 5,97·10; 5,97·10; 7,50·10 соответственно для результатов рис. 4, а, б, ж. Для результатов, представленных на рис. 4, в-е, направление движения жидкости изменяется на противоположное. Максимальная интенсивность вихрей соответственно
5,97·10; 5,97·10; 7,50·10 соответственно для результатов рис. 4, а, б, ж. Для результатов, представленных на рис. 4, в-е, направление движения жидкости изменяется на противоположное. Максимальная интенсивность вихрей соответственно ![]() 5,94·10; 4,27·10; 7,61·10; 4,63·10.
5,94·10; 4,27·10; 7,61·10; 4,63·10.
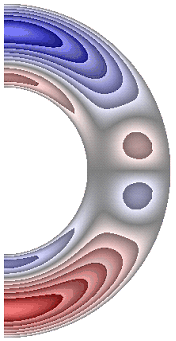
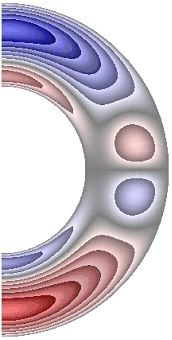
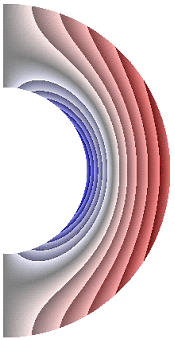
На рисунке 5 приведены результаты расчетов поля радиальной и меридиональной составляющей магнитной индукции. Радиальная составляющая магнитной индукции (рис. 5, а-е) в северном полушарии принимает отрицательные значения, за исключением небольшой области у внутренней границы слоя, а в южном – положительные, за исключением небольшой области у внутренней поверхности слоя.
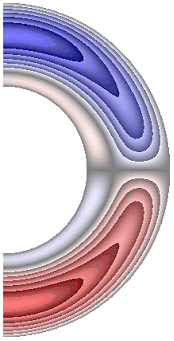
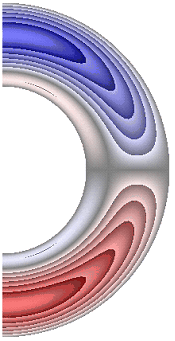
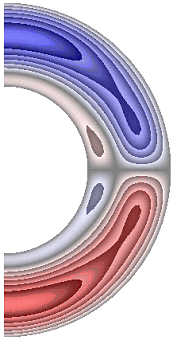
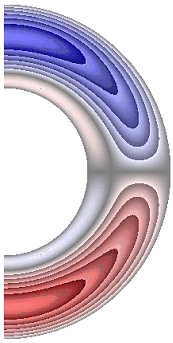
а б в г д е ж
Рисунок 5 – Поле магнитной индукции. Радиальная составляющая: а с учетом магнитных сил, ![]() б с учетом магнитных сил,
б с учетом магнитных сил, ![]() в с учетом магнитных сил,
в с учетом магнитных сил, ![]() г с учетом магнитных сил,
г с учетом магнитных сил, ![]() д с учетом магнитных сил,
д с учетом магнитных сил, ![]() е с учетом магнитных сил,
е с учетом магнитных сил, ![]() ; ж меридиональная составляющая
; ж меридиональная составляющая
Для результатов рис. 5, а и 5, е в экваториальной части слоя образуются две локальные зоны, в которых значения радиальной составляющей магнитной индукции изменяют свой знак (с минуса на плюс и с плюса на минус). Меридиональная составляющая магнитной индукции (рис. 5, ж) принимает положительные значения практически во всем слое, за исключением небольшой области у внутренней границы, в которой значения меридиональной составляющей магнитной индукции отрицательные. Оказалось, что качественно и количественно структура поля меридиональной составляющей магнитной индукции практически не изменяется для рассмотренных режимов. Максимальная интенсивность радиальной составляющей ![]() 4,00·10-4; 5,80·10-4; 5,61·10-4; 5,94·10-4; 5,62·10-4; 3,76·10-4 соответственно для результатов рис. 5, а-е, а меридиональной
4,00·10-4; 5,80·10-4; 5,61·10-4; 5,94·10-4; 5,62·10-4; 3,76·10-4 соответственно для результатов рис. 5, а-е, а меридиональной ![]() 1,00·10-2.
1,00·10-2.
Представленные выше результаты получены для значения числа Грасгофа ![]() Ниже приведены результаты, позволяющие проследить влияние увеличения интенсивности конвекции на тепловые и гидродинамические процессы в слое.
Ниже приведены результаты, позволяющие проследить влияние увеличения интенсивности конвекции на тепловые и гидродинамические процессы в слое.
На рисунках 610 приведены результаты для ![]() Значения остальных безразмерных критериев подобия не изменялись.
Значения остальных безразмерных критериев подобия не изменялись.
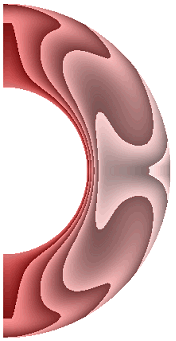
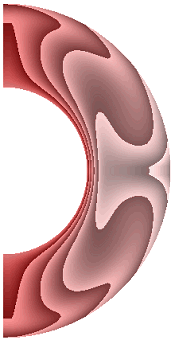
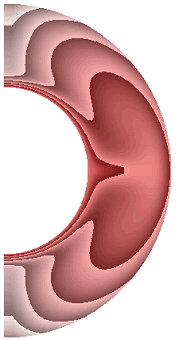
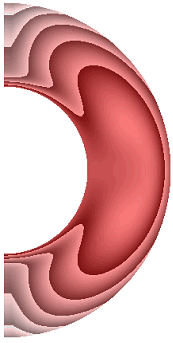
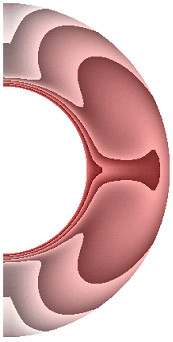
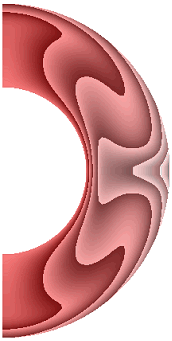
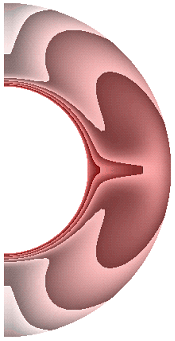
На рисунке 6 приведены результаты расчетов поля температуры.
а б в г д е ж
Рисунок 6 – Поле температуры: а без учета магнитных сил, ![]() б с учетом магнитных сил,
б с учетом магнитных сил, ![]() в с учетом магнитных сил,
в с учетом магнитных сил, ![]() г с учетом магнитных сил,
г с учетом магнитных сил, ![]() д с учетом магнитных сил,
д с учетом магнитных сил, ![]() е с учетом магнитных сил,
е с учетом магнитных сил, ![]() ж с учетом магнитных сил,
ж с учетом магнитных сил, ![]()
Перенос энергии в слое для всех режимов осуществляется конвекцией. Структура поля температуры изменяется в зависимости от режима. Диапазон изменения температуры для результата рис. 6, а (7,566; 1). Такая же качественная и количественная ситуация сохраняется и для электропроводной жидкости (рис. 6, б). Учет джоулевой диссипации (рис. 6, в) изменяет поле температуры. Диапазон изменения температуры (8,399; 1). Учет внутренних источников и стоков тепла, совместно с учетом джоулевой диссипации (рис. 6, г, д), приводит к дальнейшему изменению поля температуры. Диапазон изменения температуры для результата рис. 6, г (5,196; 1,472), а для результата рис. 6, д (11,373; 1). Неучет джоулевой диссипации, несмотря на наличие внутренних источников (стоков) тепла (рис. 6, е, ж), изменяет поле температуры. Диапазон изменения температуры для результата рис. 6, е (4,696; 1), а для результата рис. 6, ж диапазон изменения температуры (12,571; 1).
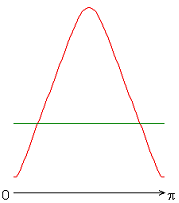
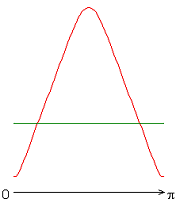
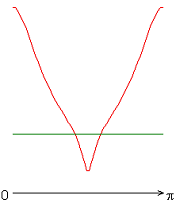
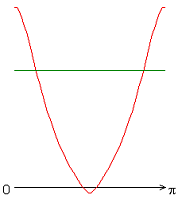
На рисунке 7 приведены распределения чисел Нуссельта. Распределения локальных чисел Нуссельта на внутренней границе слоя имеют или максимум (рис. 2, а, б, е), или минимум (рис. 2, в-д, ж) при значении полярного угла ![]() .
.
а б в г
д е ж
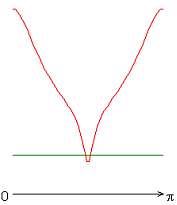
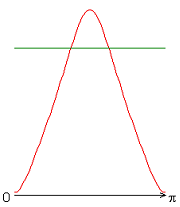
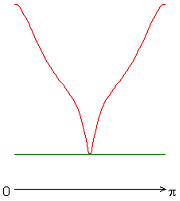
Рисунок 7 – Распределение локальных чисел Нуссельта: а без учета магнитных сил, ![]() б с учетом магнитных сил,
б с учетом магнитных сил, ![]() в с учетом магнитных сил,
в с учетом магнитных сил, ![]() г с учетом магнитных сил,
г с учетом магнитных сил, ![]() д с учетом магнитных сил,
д с учетом магнитных сил, ![]() е с учетом магнитных сил,
е с учетом магнитных сил, ![]() ж с учетом магнитных сил,
ж с учетом магнитных сил, ![]()
Учет джоулевой диссипации, совместно с учетом источников и стоков тепла (рис. 7, в-д), изменяет распределение локальных чисел Нуссельта по сравнению с результатами рис. 7, а, б. Неучет джоулевой диссипации (рис. 7, е, ж) приводит к изменению распределения локальных чисел Нуссельта. Значение осредненного и диапазон изменения локальных чисел Нуссельта следующие:
![]() 37,599; 4,485
37,599; 4,485![]() 53,542;
53,542; ![]() 37,599; 4,485
37,599; 4,485![]() 53,542;
53,542;
![]() 28,950; 7,622
28,950; 7,622![]() 63,279;
63,279; ![]() 7,750; 0,897
7,750; 0,897![]() 30,684;
30,684;
![]() 50,174; 16,495
50,174; 16,495![]() 94,693;
94,693; ![]() 16,197; 0,382
16,197; 0,382![]() 25,214;
25,214;
![]() 59,004; 20,688
59,004; 20,688![]() 106,304 соответственно для результатов рис. 7, а-ж.
106,304 соответственно для результатов рис. 7, а-ж.
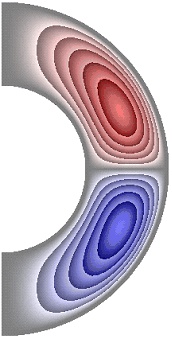
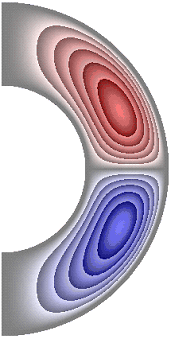
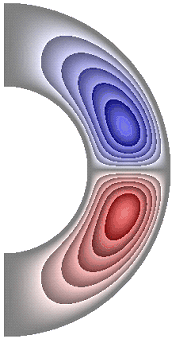
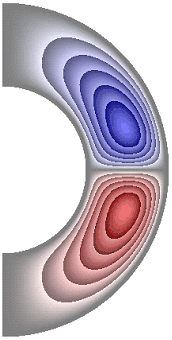
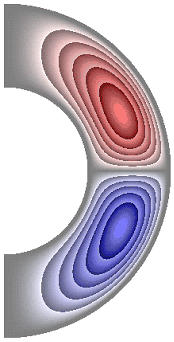
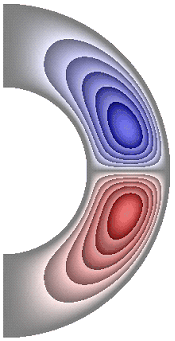
На рисунке 8 приведены результаты расчетов поля функции тока. Для всех случаев в слое образуются две конвективные ячейки.

а б в г д е ж
Рисунок 8 – Поле функции тока: а без учета магнитных сил, ![]() б с учетом магнитных сил,
б с учетом магнитных сил, ![]() в с учетом магнитных сил,
в с учетом магнитных сил, ![]() г с учетом магнитных сил,
г с учетом магнитных сил, ![]() д с учетом магнитных сил,
д с учетом магнитных сил, ![]() е с учетом магнитных сил,
е с учетом магнитных сил, ![]() ж с учетом магнитных сил,
ж с учетом магнитных сил, ![]()
Для результатов, представленных на рис. 8, а, б, е, жидкость в северном полушарии слоя движется против часовой стрелки (значения функции тока положительные), а в южном – по часовой стрелке (значения отрицательные). Максимальное значение функции тока соответственно ![]() 2,08·10; 2,08·10; 1,63·10. Учет джоулевой диссипации (рис. 8, в), так же как и учет внутренних источников и стоков тепла, совместно с учетом джоулевой диссипации (рис. 8, г, д), изменяет направление циркуляции жидкости в ячейках на противоположное. Максимальное значение функции тока для результатов рис. 8, в-д
2,08·10; 2,08·10; 1,63·10. Учет джоулевой диссипации (рис. 8, в), так же как и учет внутренних источников и стоков тепла, совместно с учетом джоулевой диссипации (рис. 8, г, д), изменяет направление циркуляции жидкости в ячейках на противоположное. Максимальное значение функции тока для результатов рис. 8, в-д ![]() 1,89·10; 1,40·10; 2,26·10. Неучет джоулевой диссипации, при учете внутренних источников тепла (рис. 8, е), изменяет направление циркуляции жидкости, а учет внутренних стоков тепла (рис. 8, ж) сохраняет направление циркуляции жидкости, по сравнению с результатами рис. 8, в-д. Максимальное значение функции тока для результата рис. 8, ж
1,89·10; 1,40·10; 2,26·10. Неучет джоулевой диссипации, при учете внутренних источников тепла (рис. 8, е), изменяет направление циркуляции жидкости, а учет внутренних стоков тепла (рис. 8, ж) сохраняет направление циркуляции жидкости, по сравнению с результатами рис. 8, в-д. Максимальное значение функции тока для результата рис. 8, ж ![]() 2,39·10.
2,39·10.
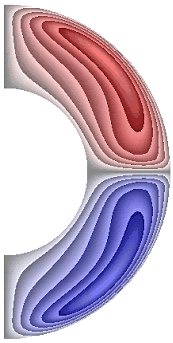
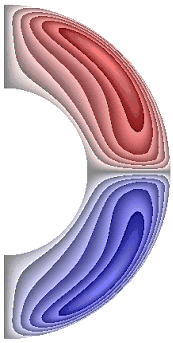
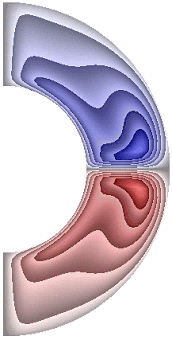
На рисунке 9 приведены результаты расчетов поля напряженности вихря.
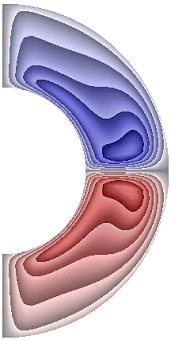
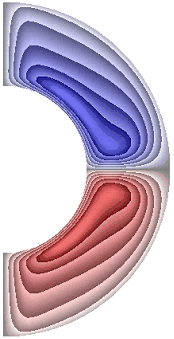
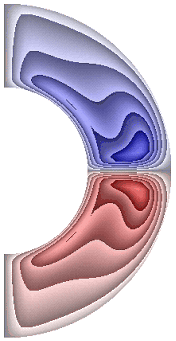
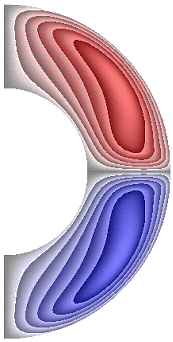
а б в г д е ж
Рисунок 9 – Поле напряженности вихря: а без учета магнитных сил, ![]() б с учетом магнитных сил,
б с учетом магнитных сил, ![]() в с учетом магнитных сил,
в с учетом магнитных сил, ![]() г с учетом магнитных сил,
г с учетом магнитных сил, ![]() д с учетом магнитных сил,
д с учетом магнитных сил, ![]() е с учетом магнитных сил,
е с учетом магнитных сил, ![]() ж с учетом магнитных сил,
ж с учетом магнитных сил, ![]()
В слое (рис. 9, а, б, е) образуются два крупномасштабных вихря, в которых жидкость движется против часовой стрелки (значения положительные) в северном полушарии, и по часовой стрелке (отрицательные значения) – в южном. Максимальная интенсивность этих вихрей ![]() 2,43·102; 2,43·102; 1,64·102 соответственно для результатов рис. 9, а, б, е. Для результатов, представленных на рис. 9, в-д, ж, образуются два среднемасштабных вихря. В северном полушарии жидкость движется по часовой стрелке (значения отрицательные) а в южном – против часовой стрелки (значения положительные). Максимальная интенсивность вихрей составляет величину
2,43·102; 2,43·102; 1,64·102 соответственно для результатов рис. 9, а, б, е. Для результатов, представленных на рис. 9, в-д, ж, образуются два среднемасштабных вихря. В северном полушарии жидкость движется по часовой стрелке (значения отрицательные) а в южном – против часовой стрелки (значения положительные). Максимальная интенсивность вихрей составляет величину ![]() 2,32·102; 1,68·102; 2,96·102; 3,23·102 соответственно. Неучет джоулевой диссипации при наличии внутренних источников тепла приводит к изменению направления циркуляции жидкости (рис. 9, е).
2,32·102; 1,68·102; 2,96·102; 3,23·102 соответственно. Неучет джоулевой диссипации при наличии внутренних источников тепла приводит к изменению направления циркуляции жидкости (рис. 9, е).
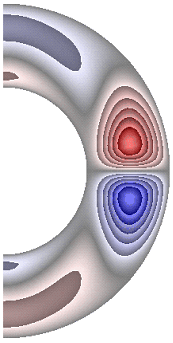
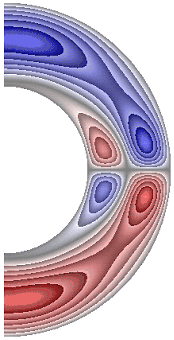
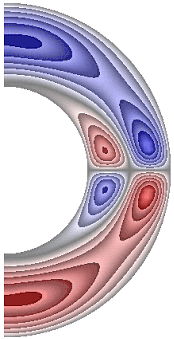
На рисунке 10 приведены результаты расчетов поля радиальной составляющей магнитной индукции.

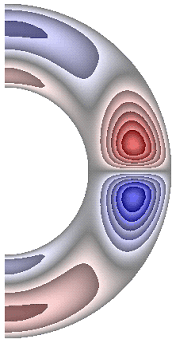
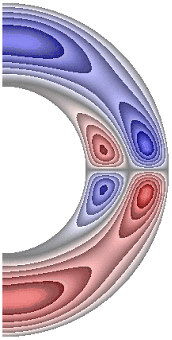
а б в г д е
Рисунок 10 – Поле радиальной составляющей магнитной индукции: а с учетом магнитных сил, ![]() б с учетом магнитных сил,
б с учетом магнитных сил, ![]() в с учетом магнитных сил,
в с учетом магнитных сил, ![]() г с учетом магнитных сил,
г с учетом магнитных сил, ![]() д с учетом магнитных сил,
д с учетом магнитных сил, ![]() е с учетом магнитных сил,
е с учетом магнитных сил, ![]()
Значения радиальной составляющей магнитной индукции (рис. 10) в северном полушарии отрицательные, за исключением небольшой области у внутренней границы слоя, а в южном – положительные, за исключением небольшой области у внутренней границы. Для результатов рис. 10, а, д в экваториальной части слоя образуются две локальные зоны, в которых значения радиальной составляющей магнитной индукции изменяют свой знак (с минуса на плюс и с плюса на минус). Максимальная интенсивность радиальной составляющей ![]() 1,13·10-3; 9,15·10-4; 8,58·10-4; 1,06·10-3; 8,35·10-4; 1,12·10-3 соответственно для результатов рис. 10, а-е.
1,13·10-3; 9,15·10-4; 8,58·10-4; 1,06·10-3; 8,35·10-4; 1,12·10-3 соответственно для результатов рис. 10, а-е.
На рисунке 11 приведены результаты расчетов поля меридиональной составляющей магнитной индукции. Значения меридиональной составляющей (рис. 11) положительные практически во всем слое, за исключением небольшой области у внутренней границы слоя, в котором ее значения отрицательные. В зависимости от режима поле меридиональной составляющей магнитной индукции претерпевает, хотя и незначительные, изменения. Эти изменения происходят в экваториальной плоскости, проявляясь в увеличении зоны отрицательных значений меридиональной составляющей, похожей на треугольник, вершина которого стремится к внешней границе слоя. Максимальная интенсивность меридиональной составляющей не превышает значения ![]() 1,00·10-2.
1,00·10-2.

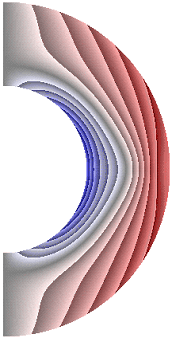

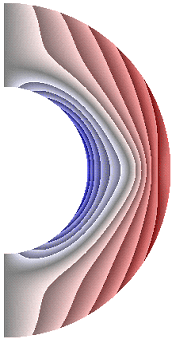
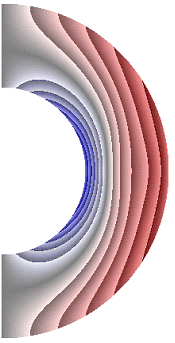
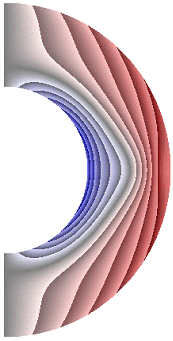
а б в г д е
Рисунок 11 – Поле меридиональной составляющей магнитной индукции: а с учетом магнитных сил, ![]() б с учетом магнитных сил,
б с учетом магнитных сил, ![]() в с учетом магнитных сил,
в с учетом магнитных сил, ![]() г с учетом магнитных сил,
г с учетом магнитных сил, ![]() д с учетом магнитных сил,
д с учетом магнитных сил, ![]() е с учетом магнитных сил,
е с учетом магнитных сил, ![]()
Анализ результатов, полученных по предложенной математической модели, позволяет сделать следующие выводы:
для всех режимов в слое образуются две конвективные ячейки и два вихря;
учет электропроводности жидкости (без учета других факторов) не влияет на теплообмен и гидродинамику жидкости в слое;
учет джоулевой диссипации изменяет направление циркуляции жидкости в ячейках;
в структуре радиальной составляющей магнитной индукции при: ![]() ,
, ![]() и
и ![]() образуются две дополнительные зоны;
образуются две дополнительные зоны;
интенсификация конвекции в слое влияет на структуру меридиональной составляющей магнитной индукции;
математическая модель и полученные результаты могут быть полезными при исследовании тепловых и гидродинамических процессов в недрах Земли и других планет.
Библиографический список
- Жарков В. Н. Внутреннее строение Земли и планет, М., Наука. 1983.
- Жарков В. Н., Трубицын В. П., Самсоненко Л. В. Физика Земли и планет. Фигуры и внутреннее строение, М., Наука, 1971.
- Яновский Б. М. Земной магнетизм, Л., Изд-во Ленигр. ун-та, 1978.
- Соловьев С. В. Моделирование конвективного теплообмена в жидком ядре Земли. Вестник Тихоокеанского государственного университета. 2012. № 2 (25). С.73-82.
- Госмен А. Д., Пан В. М., Ранчел А. К., Сполдинг Д. Б., Вольфштейн М. Численные методы исследования течений вязкой жидкости, М., Мир, 1972.
