Приводятся некоторые образцы практических задач по формированию профессиональных компетенций [1…5] при изучении дифференциального исчисления в рамках курса математики по стандартам ФГОС 3+ по направлению 08.03.01 – Строительство.
1. Пусть стоимость 1 м² фасада составляет а рублей, для других стен – b рублей, а стоимость крыши в пересчете на 1 м² ее основания равна с рублей. Определить соотношения между длиной, шириной и высотой для углового дома объемом v м³ так, чтобы стоимость его стен и плоской крыши была наименьшей.
Угловой дом имеет по фасаду две стены. Будем полагать, что основание дома – прямоугольник длиной х м и шириной у м, высота дома равна  м.
Тогда площадь двух стен по фасаду равна

,

а площадь двух других – . При этом площадь основания крыши равна ху.
Искомая стоимость стен и крыши

или

.

Необходимые условия экстремума будут иметь вид:

Откуда

Из равенства правых частей будем иметь

.

С учетом  получим

.

Так что основанием дома должен быть квадрат со стороной, равной .
Из предыдущего определится отношение между стороной основания и высотой дома:

,

т.е. отношение сторон квадрата к высоте дома должно быть равно . Без каких-либо исследований ясно, что при полученных размерах дома достигается минимум стоимости.

2. Требуется сделать открытый цилиндрический резервуар объемом V. Стоимость материала, из которого делается дно резервуара, в m раз больше стоимости материала, идущего на его боковые стенки. При каких размерах резервуара стоимость его будет минимальной?
Развернутая поверхность открытого сверху цилиндра состоит из нижнего основания  и боковой поверхности . Стоимость резервуара опре­делится поверхностью используемого материала

.

Задача свелась к определению минимума функции у при условии .
С учетом  будем иметь:

.

Дифференцируя по R и приравняв производную нулю, найдем единственный корень полученного уравнения:

Откуда

Таким образом, искомая стоимость будет минимальной, если высота цилиндра будет в m раз превышать радиус его основания:

.

В том, что найденное  доставляет минимум функции у, легко убедиться, определив знак второй производной в критической точке:

В частном случае, с другой стороны, при m=1 минимальная стоимость достигается при минимальном расходе материала. Для того, чтобы изготовить открытый цилиндр заданного объема V с затратой минимального количества материала, надо высоту цилиндра взять равной его радиусу. Необходимый для этого расход материала (не учитывая запаса на изготовление швов) определяется по формулам:

 при m=1.

3. Какие размеры надо придать цилиндрической емкости с крышкой данного объема V, чтобы поверхность была наименьшей?
Пусть r – радиус основания цилиндра, h – высота цилиндра (величины r и h – переменные; если придать r какое-либо значение, то h определится из условия, что емкость цилиндра равна V; , ).
Поверхность емкости S состоит из двух оснований, площадь которых равна , и боковой поверхности, площадь которой равна , т.е.

.

Найдем минимум функции S(r) (V задано!):

Так что , если .
Откуда .
Имеем .
Из  следует  т.е. S(r) имеет минимум.
Следовательно, поверхность емкости минимальна при

 и .

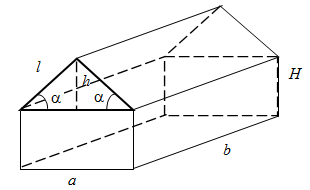
4.Для хранения техники необходимо построить поме­щение прямоугольной формы с площадью 200 м², высота стены 3 м, крыша равноскатная на обе стороны под углом 30 к горизонту, без потолка. Определить размеры помещения, при которых расход материалов будет минимальным.
Примем за критерий эффективности общую площадь поверх­ности помещения.

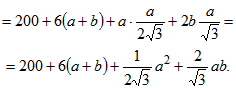
С учетом

получим

Из  получим

Решив полученное уравнение, находим

Из  следует, что указанным а и b соответствует минимальный расход материалов.
Приведенные примеры можно рассматривать в качестве иллюстрации методической основы для подбора и других прикладных задач, способствующих формированию общепрофессиональных компетенций в рамках прикладного бакалавриата, в том числе с учетом междисциплинарных связей и непрерывности фундаментальной подготовки.

1. Данилов А.М., Гарькина И.А., Маркелова И.В. Методологические принципы оценки качества образовательной системы / Современные проблемы науки и образования. – 2014. – № 2. URL: http://www.science-education.ru/116-12335
2. Гарькина И.А., Данилов А.М.  Системный подход к повышению качества образования / Вестник КГУ им. Н.А. Некрасова. – 2013. – №4. –  Т. 19. –  С. 4-7
3. Данилов А.М., Гарькина И.А. Образовательная система с позиций идентификации и управления / Региональная архитектура и строительство. –  2013. –  № 2. –  С. 143-146.
4. Данилов А.М., Гарькина И.А., Маркелова И.В. Междисциплинарные связи при компетентностном подходе к подготовке бакалавров // Современные проблемы науки и образования. – 2014. – № 3;URL: http://www.science-education.ru/117-13065
5. Данилов А.М., Гарькина И.А. Теория вероятностей и математическая статистика с инженерными приложениями: учебное пособие / –  Пенза: ПГУАС. – 2010. – 228 с.

Все статьи автора «fmatem»