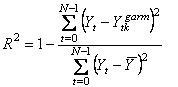Необходимой предпосылкой развития экономики и инноваций является наличие высокообразованных кадров. Именно высокообразованные работники представляют наиболее мобильную группу, что неизбежно ведет к миграционному оттоку.
Управление трудовыми ресурсами региона предполагает знание не только количественных параметров миграционных процессов, но и тенденций этих процессов на ближайшую и отдаленную перспективу.
Остановимся на способе рассмотрения миграционных процессов исходя из их цикличности. При суммировании циклических составляющих данного процесса возможно описание его динамики, а так же планирование ее изменения с помощью экстраполяции суммы гармоник.
Зная количество мигрантов по месяцам, составим ряд данных:
затем с помощью метода наименьших квадратов рассчитаем уравнение линии тренда:
Воспользуемся следующими формулами:
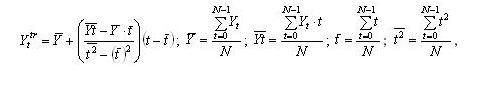где – среднее арифметическое значение времени ряда;
– среднее арифметическое значение временного ряда.
Исходная модель, описывающая ряд динамики будет представлять собой тренд:
Чтобы снять направленность временного ряда, необходимо из исходного ряда вычесть исходный линейный тренд Ytr
Таким образом, центрированный временной ряд будет иметь вид:
Перейдем к выделению гармоники Ykgarm с параметрами
которая в общей дисперсии будет обеспечивать наибольшую долю дисперсии зависимой переменной.
Определение наибольшей доли дисперсии зависимой переменной в общей дисперсии произведем с помощью коэффициента детерминации R2 по формуле:
Из каждого цикла выберем гармоникуYk*=Ykgarm с наибольшим R2 и добавим в модель, описывающую ряд динамики :
Затем «очистим» ряд, вычитая эти гармоники из центрированного ряда . Таким образом, образовался новый ряд:
Теперь с помощью статистики Дарбина-Уотсона сделаем вывод об отсутствии автокорреляции остатков:
Сравним полученное значение DW с табличным. В случае выполнения условия 
(где d(N,α) – табличное значение статистики Дарбина-Уотсона, α - уровень значимости, N – длина ряда) добавление гармоник следует прекратить, т.к. остатки «чистого» ряда носят случайный характер. [1, 63-65]
Таким образом, можно говорить о том, что все зависимости ряда определены.
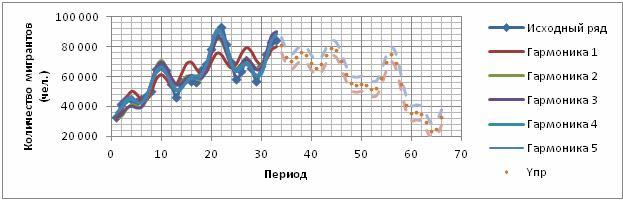
Следуя приведенному алгоритму, установлен следующий моделируемый временной ряд:
По установленной зависимости Y(ti) на отрезке t є [0;N-1], представляется возможным посчитать значения Y(ti) на следующем временном отрезке t є [N;N+m] , где m – прогнозный период. Отметим, что при большем «горизонте», точность прогноза ниже, поэтому мы строим прогноз только на 2 года.
Рисунок 1. Моделируемый временной ряд
В целом количество мигрантов снижается, однако выявляемые миграционные установки свидетельствуют об уровне потенциальной миграции, которая имеет вполне реальные социально-экономические последствия.
Среди процессов миграции населения и трудовых ресурсов последнего периода значительное место занимает миграция высококвалифицированных специалистов.
Что же играет ключевую роль на желание мигрировать в большей степени?
Для ответа на данный вопрос воспользуемся данными, полученными в результате собственных социологических исследований, проведенных среди студентов и молодых ученых (2011-2012гг). В опросе приняли участие 485 студентов и 35 молодых ученых СГАУ, 47 студентов Московского авиационного института.
В качестве факторов (xi), влияющих на эмиграционные намерения (У), были взяты самые распространенные ответы респондентов на вопрос «Каковы причины эмиграционных намерений», а так же их пол, возраст и их материальное положение.
Сгруппировав показатели, определим корреляционные связи в группах, чтобы сделать вывод о возможности совместного применения данных групп для построения статистических моделей прогнозирования динамики.
Проведение корреляционного анализа выявило 5 наименее коррелированных предикторов, имеющих наибольшее влияние на регрессор (миграционное намерение), которые представлены в таблице 1.
Таблица 1. Факторы, влияющие на эмиграционные намерения
|
Фактор |
Обозначение |
|
х1 |
пол |
|
х2 |
возраст |
|
х3 |
материальное положение |
|
х4 |
отсутствие работы по профессии |
|
х5 |
рост преступности |
|
х6 |
качество жизни |
Прейдем к проверке гипотезы о наличии мультиколлинеарности в модели. Мультиколлинеарность факторов тем сильнее, чем ближе к нулю определитель матрицы межфакторной корреляции, а значит результаты множественной регрессии более ненадежны.
Пошагово отберем основные объясняющие переменные. В основе данного отбора лежит критерий:
Множественный коэффициент корреляции находится по следующей формуле:
где R – корреляционная матрица размера (р+1)x(р+1), R=[rkl], ,
R00 – алгебраическое дополнение элемента r00 (первая строка и первый столбец матрицы соответствуют результирующей переменной у.
Далее с помощью априорного метода построения уравнения множественной регрессии, который заключается в дополнительном введении факторов получено уравнение множественной регрессии факторов, влияющих на миграционные намерения.
Уравнение регрессии, описывает 75% данных и является значимым исходя из коэффициента Фишера и t-cтатистики.
Окончательное уравнение множественной регрессии имеет вид:
По результатам анализа наиболее значимым фактором является качество жизни. В порядке убывания значимости можно перечислить такие факторы как рост преступности, отсутствие работы по профессии, возраст, материальное положение, пол респондентов.
Библиографический список
- Ситникова, А.Ю. Модель и алгоритмы управления операционной деятельностью брокерской компании на основе спектрального анализа и цифровой фильтрации: дис. канд. эк. наук: 08.00.13 [Текст] / Ситникова Анастасия Юрьевна. – Самара, 2010. – 158 с.