При идентификации эргатических систем особенно актуальны решения задач, связанных с дискретизацией непрерывных сигналов и возможностью восстановления непрерывной функции  по ее спектру. 
Если функции  имеют ограниченный спектр, то вместо мгновенных значений можно использовать коэффициенты разложения в ряд Фурье (часто это используется при составлении вибрационных карт сложных конструкций). Здесь реакции подсистем обычно представляются экспоненциально-косинусными выражениями. 
При определении параметров управляемого объекта часто используется метод пробных воздействий (в частности, используется реакция  объекта на отклонение органа управления). В этом случае задача во многом сводится к применению теоремы В.А.Котельникова для простейшего случая квантования сигнала

 или ,

 - амплитуда,  (-постоянная времени).
При определении частоты квантования предполагается, что спектр частот рассматриваемого сигнала ограничен частотой  (выбирается из условия, что энергия суммы отброшенных гармоник не превышает энергии ошибки). В предположении, что ошибка восстановления сигнала по его квантованным значениям не должна превышать  (- шаг квантования по уровню,  - коэффициент). Тогда полная энергия  сигнала  определится в виде суммы двух слагаемых

,

(1)

 и  - соответственно энергия сигнала, ограниченного частотой , и энергия отброшенных гармоник (равна энергии ошибки воспроизведения).
Спектральная плотность для указанных видов экспонент:

; 

или

.

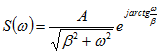Для сигнала, содержащего все гармоники от 0 до , справедливо:

,

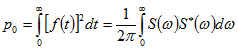где  - сопряженная с .
Откуда следует

.

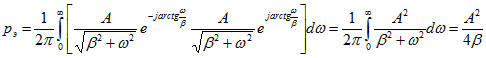Аналогично энергия сигнала , ограниченного частотой , будет иметь вид:

.

По условиям измерения любое значение сигнала в пределах от 0 до  (n – максимальное число шагов шкалы уровней) равновероятно. Так что среднее значение  определится в виде:

.

Тогда среднее значение энергии ошибки воспроизведения (предполагается, что любое значение энергии ошибки в пределах заданной величины  равновероятно) имеет вид:

.

В силу предыдущего:

,

- относительная ошибка.
Подставляя значения ,, в (1), получим:

,
,
.

Из последнего выражения следует

или

.

С учетом  и , имеем:

.

Искомая частота квантования в соответствии с теоремой В.А.Котельникова определится в виде:

(частота квантования экспоненциального сигнала зависит от заданной ошибки воспроизведения). В предположении восстанавливаемости сигнала внутри интервалов квантования  ошибка квантования порождается только за счет ограничения спектра частот этого сигнала (при соблюдении условий теоремы).
Отметим, квантование по времени фактически сводится к аппроксимации функции  в заданном классе . В частности, можно построить полином  степени , принимающий в точках те же значения, что и функция :

.

Задача сводится к определению коэффициентов  () полинома

Из уравнений

,
,
……………………………….
.

Предложенные методики широко использовались в задачах определения параметров управляющих воздействий (непрерывные функции, поток импульсов, выбросы и т.д.), связанных с оценкой имитационных характеристик тренажных и обучающих комплексов для подготовки операторов различных управляемых в пространстве объектов [1…5].

1. Данилов А.М., Гарькина И.А.Теория вероятностей и математическая статистика с инженерными приложениями. – Пенза: ПГУАС. – 2010.  – 228 с.
2. Гарькина И.А., Данилов А.М., Домке Э.Р. Математическое моделирование управляющих воздействий оператора в эргатической системе / Вестник Московского автомобильно-дорожного государственного технического университета (МАДИ). – 2011. – № 2. – С. 18-23.
3. Гарькина И.А., Данилов А.М., Пылайкин С.А.Тренажеры и имитаторы транспортных систем: выбор параметров вычислений, оценка качества / Мир транспорта и технологических машин. 2013. № 3 (42). С. 115-120.
4. Будылина Е.А., Гарькина И.А., Данилов А.М., Пылайкин С.А. Аналитическое определение имитационных характеристик тренажных и обучающих комплексов / Фундаментальные исследования. – 2014. – № 6-4. – С. 698-702.
5. Гарькина И.А., Волкова Т.Н. Опыт оптимизации многоцелевой системы / Современные научные исследования и инновации. –  2014. –  № 10-1 (42). –  С. 120-124.

Все статьи автора «fmatem»