В литературе, посвященной теории автоматического управления, вопросам синтеза регуляторов традиционно уделяется много внимания. В наши дни появилось большое количество методов синтеза регуляторов, разнообразных по своим постановкам и результатам. Вместе с тем, в современных исследованиях отчетливо наблюдается тенденция перехода от простых объектов управления (которые описываются дифференциальными уравнениями до второго порядка включительно) к сложным (имеющим более высокий порядок). При этом традиционные методы синтеза (такие как методы синтеза ПИ- и ПИД – регуляторов) для объектов высокого порядка не всегда дают удовлетворительный результат: повышая порядок объекта мы должны адекватно повышать и порядок регулятора. В связи с этим особое значение приобретают методы синтеза модальных регуляторов, позволяющие рассчитать регулятор для объекта сколь угодно высокого порядка [1, 2].

Методы синтеза модальных регуляторов были разработаны еще в 70-х годах (отметим, что одной из первых работ в этом направлении является работа Кузовкова Н.Т. [3]) и многие из них приводятся в современной технической литературе [4-6]. Сейчас данные методы относятся к разряду классических. Задача модального управления связана с построением регулятора, при котором полюса передаточной функции (или в многомерном случае, собственные числа матрицы) замкнутой системы располагаются в заданных точках или заданных областях комплексной плоскости.

Суть модального управления состоит в нахождении численных значений коэффициентов передачи безынерционных обратных связей (ОС) по всем переменным состояния объекта для того, чтобы обеспечить заданное распределение корней характеристического уравнения замкнутой САУ.

Корни характеристического уравнения САУ целиком определяют ее свободное движение.

Каждая составляющая такого движения, соответствующая отдельному корню p_i (или паре комплексно сопряженных корней), за рубежом называется модой – отсюда и появилось понятие «модальное управление». Корни характеристического уравнения имеют прямую зависимость от его коэффициентов, поэтому модальное управление можно рассматривать как целенаправленное изменение коэффициентов характеристического уравнения объекта при помощи безинерционных ОС.

В настоящее время в связи с увеличением мощности вычислительной техники появляется множество различных методов расчёта и алгоритмов, достаточно легко реализуемых программно, но в то же время позволяющих быстро и качественно решать задачи, заменяя собой громоздкий расчёт. Одним из наиболее перспективных является метод генетических алгоритмов.

Генетический алгоритм (ГА) – это в первую очередь алгоритм эволюции, другими словами, основной особенностью алгоритма является скрещивание (комбинирование). Несложно догадаться, что идея алгоритма взята у природы – путем перебора, а затем – отбора, получается правильная «комбинация». Алгоритм можно разделить на три этапа:

• Скрещивание
• Селекция (отбор)
• Формирования нового поколения

Если результат не удовлетворяет нашим требованиям, эти шаги повторяются до тех пор, пока результат не начнет нас устраивать или произойдет одно из ниже перечисленных условий:

• Число поколений (циклов) достигнет заранее выбранного максимума
• Будет исчерпано время на мутацию [7]

Формально ГА можно описать следующим образом (1):

,  (1)

где  - исходная популяция, где

 - решение задачи, представленное в виде хромосомы;

 - целое число (размер популяции);

 - целое число (длина каждой хромосомы популяции);

 - оператор отбора;

 - отображение, определяющее рекомбинацию (кроссинговер и мутацию);

 - целевая функция;

– критерий остановки.

 является случайно сгенерированной начальной популяцией, и параметры  и  описывают количество индивидуумов одного поколения и длину (размер) каждого индивидуума популяции соответственно.

Оператор отбора  порождает промежуточную популяцию  из популяции с помощью отбора и генерации новых копий элементов : . Целевая функция обеспечивает обратную связь от результатов оптимизации в течении поколения , а также используется для отбора конкурентоспособных индивидуумов популяции.

После завершения отбора выполняются генетические операции кроссинговера и мутации. Две эти операции носят случайный характер (вероятность применения, выбор локуса внутри хромосомы). Соответственно элементу  выбирается партнер из  для рекомбинации, если это необходимо (например, для кроссинговера) и происходит образование новой хромосомы. Операторы, которые приводят после своего завершения к более, чем одному потомку, случайно или используя какую-то другую стратегию, отбирают одного или нескольких элементов – потомков, которые будут окончательным результатом операции, остальные элементы отбрасываются.

Одноточечный кроссинговер выполняется следующим образом:

1)      Случайный выбор партнера для скрещивания (2)

 из ; (2)

2)      Случайный выбор точки кроссинговера (3)

; (3)

3)      Формирование двух новых индивидуумов (4)

 и

; (4)

4)      Случайный выбор (5)

(5)

 Кроссинговер контролирует баланс между дальнейшим использованием уже найденных хороших подобластей пространства и исследованием новых подобластей. Достигается это за счет неразрушения общих блоков внутри хромосом – родителей, сохраняющих «хорошие» паттерны и одновременном исследовании новых областей в результате обмена частями строк (хромосом).

Мутации вносят новизну и предотвращают невосстановимую потерю аллелей в определенных позициях, которые не могут быть восстановлены кроссинговером, тем самым ограничивая преждевременное сжатие пространства поиска. Мутация представляет собой случайное изменение части хромосомы, его вероятность довольно низкая. Процесс мутации описан ниже:

1)      Случайный выбор (с некоторой фиксированной вероятностью) позиций (6)

(6)

внутри битовой строки, подверженной мутации;

2)                                                                                                                                                       , (7)

где  выбираются случайным образом.

Процесс мутации может рассматриваться как переход между различными состояниями пространства поиска и характеризоваться условной плотностью вероятности нового состояния при данном старом.

Остановка эволюции может произойти, если, например, получено удовлетворительное решение, число поколений достигло определённого значения, сходимость происходит с очень низкой скоростью и т. п.) [8].

Вернёмся к теме данной статьи. Суть проблемы такова: имеется модель электропривода. Задача состоит в том, чтобы при моделировании режима отработки электроприводом определенного задания получить приемлемый результат, а затем разработать генетический алгоритм и программу в среде Matlab, которая бы отрабатывала это же задание с минимальной погрешностью. С точки зрения модального управления эта задача решается нахождением коэффициентов модального регулятора СУЭП, рассчитываемых через корни характеристического уравнения. Эти коэффициенты должны быть подобраны так, чтобы переходный процесс удовлетворял некоторым заданным критериям (по скорости, перерегулированию и т.д.) В качестве альтернативного  варианта предлагается использование генетического алгоритма для подбора коэффициентов ОС системы модального управления. В этом случае отпадёт необходимость в громоздких расчётах, программа сформирует требуемые коэффициенты обратных связей автоматически. Отметим, что для реализации этого метода необходимо достаточно мощное вычислительное устройство – это позволит затратить меньшее время на решение задачи в “реальном времени”.

Работа генетического алгоритма управляется тремя операторами: селекцией, скрещиванием и мутацией (рис. 1).

В общем случае первоначальная генерация популяции длиной N осуществляется случайным образом в исследуемой области решений. После этого начинается циклическая работа генетического алгоритма.

Селекция (отбор, репродукция) – первая операция, осуществляемая над популяцией. В результате селекции должны быть отобраны хромосомы-участники процесса генерации новой популяции (популяции потомков). Селекция происходит на основании оценок пригодности хромосом. В результате появляется промежуточная популяция (родительский пул). Промежуточная популяция – это набор особей, получивших право на размножение. Приспособленные особи могут быть записаны туда не один раз. «Плохие» особи скорее всего не попадут в промежуточную популяцию.

После селекции выполняются операции скрещивания и мутации, обобщенно называемые рекомбинацией.

Рисунок 1 – Общая структура ГА

Скрещивание (пересечение, кроссовер, кроссинговер) выполняется в целях комбинирования и смешения признаков родительской популяции в популяции потомков. В классическом генетическом алгоритме применяется одноточечный оператор кроссовера: для родительских хромосом случайным образом выбирается точка раздела, и они обмениваются отсеченными частями. Полученные две хромосомы являются потомками.

Мутация небольшого количества генов в популяции потомков призвана сообщить потомкам новые признаки, которые могли отсутствовать в родительской популяции.

Схема ГА предполагает, что получено такое же количество потомков, как количество родителей, и после выполнения мутации новая популяция полностью сформирована, так что может начинаться новый цикл развития. Однако при этом существует опасность потери наилучших хромосом, поскольку все потомки могут оказаться хуже своих родителей. Для устранения этой опасности могут быть использованы следующие приемы:

– количество потомков делается меньшим количества родителей, так что замещаются только худшие родительские хромосомы;

– генерируется большее количество потомков, чем это необходимо, после чего происходит тестирование, и только лучшие хромосомы-потомки попадают в новую популяцию вместе с лучшими родителями;

– выделяется элита популяции (порядка 10%), которая попадает в новую популяцию без изменения, выделяются наихудшие хромосомы (также 10%), которые замещаются хромосомами, сге­нерированными случайным образом, а остальные хромосомы подвергаются генетическим операциям.

Помимо операторов скрещивания и мутации в ГА может использоваться оператор инверсии.

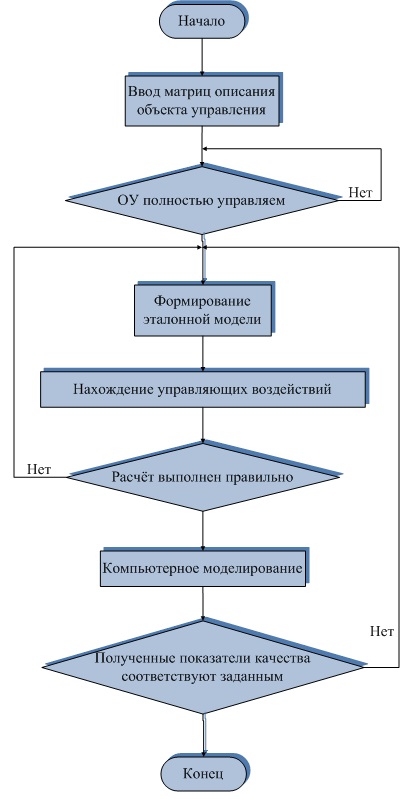
Проведём анализ особенностей варианта классической теории модального управления и варианта с использованием ГА на уровне алгоритмов этих процессов, представленных в виде блок-схем (рис. 2 и рис. 3).

Рисунок 2 – Блок-схема алгоритма нахождения коэффициентов ОС модальной САУ классическим методом

 

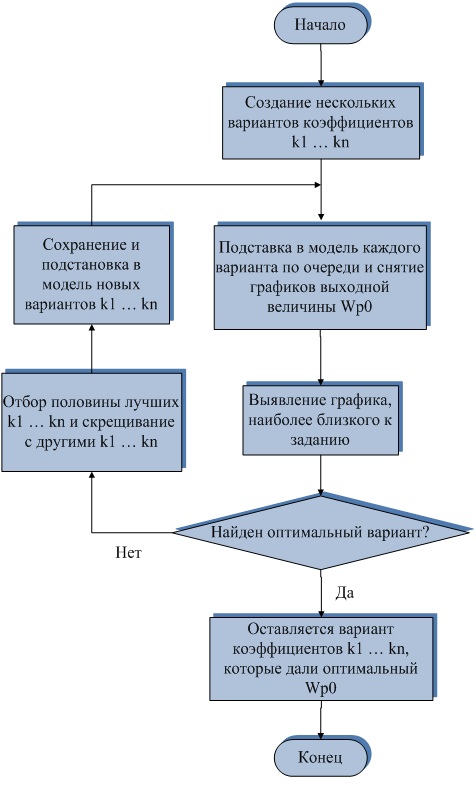
Рисунок 3 – Блок-схема алгоритма нахождения коэффициентов ОС модальной САУ методом ГА

В варианте нахождения коэффициентов ОС модальной САУ классическим методом используется матричный способ описания ОУ и формирование блока коэффициентов на основе заданной эталонной модели, согласно требуемым показателям качества переходных процессов. Недостатком метода является высокая сложность получения математических зависимостей параметров при степени характеристического уравнения САУ выше третьего и, вследствие этого, невозможность аналитического исследования полученных зависимостей.

Предлагаемый вариант структуры ГА работает согласно следующей общей схеме:

1. Для образования популяции создаётся какое-то произвольное семейство хромосом (индивидуумов).

2. Появляется новая популяция, и при этом каждая i-я популяция создаётся из (i–1)-й популяции. Для этого проделываются следующие шаги:

– для всех хромосом в популяции высчитывается значение пригодности (Fitness function);

– происходит ранжирование значений пригодности всех хромосом;

– имеющие наилучшие значения пригодности (элита) индивидуумы из текущей популяции без каких-либо изменений переходят в следующую популяцию;

– происходит отбор хромосом-родителей, чтобы создать часть новой популяции;

– хромосомы-родители производят хромосом-потомков. Одна часть лучших хромосом переходит в будущую популяцию без изменений (elite children), другая часть получается после операции мутации (mutation children), третья часть – после кроссовера (crossover children). В результате скрещивания двух хромосом получается один потомок.

3. Новая популяция заменяет старую.

4. Выполняется проверка критериев остановки алгоритма. В случае их невы­полнения происходит возврат к п. 2.

В генетическом алгоритме функцией пригодности называется минимизируемая функция ошибки, но можно взять функцию с обратным знаком, и тогда любую задачу можно рассматривать как задачу максимизации.

Индивидуум в ГА представляет собой точку, в которой возможен расчет функции пригодности. Таким образом, вектор допустимых значений, чья размерность равна числу переменных данной задачи, и есть индивидуум (хромосома). Ему соответствует определен­ная пригодность (score).

Хромосома (геном) состоит из генов. Гены – это компоненты хромосомы. Популяция представляет собой массив хромосом.

Преимуществами данного метода являются:

• отсутствие части расчётов;
• введение новых параметров системы без усложнения модели (в отличие от классического метода не нужно делать полный перерасчёт, добавится только новый массив чисел в Matlab);
• возможность автоматизации процесса настройки;
• реализация генетического алгоритма по принципу «черный ящик» также дает некоторые преимущества в плане отсутствия необходимости, а зачастую и невозможности построения сложных математических моделей объекта в виду отсутствия адекватных данных входных/выходных переменных.

К недостаткам метода можно отнести обязательное наличие мощной вычислительной техники, а также всё тот же принцип «черный ящик», т. к. невозможно классическими методами дать анализ системы, т. е. увидеть, каким образом происходит расчёт каких-либо величин и т. д.

Библиографический список

1. Кожевников А.В. Применение метода модального управления для повышения стабильности работы электромеханических систем прокатного производства // Производство проката.-№11. -2013. С. 35-40.
2. Булындин М.Г. Исследование эталонных систем модального управления // Современные научные исследования и инновации. 2013. №11 (31). С. 9.
3. Кузовков, Н.Т. Модальное управление и наблюдающие устройства – Москва, «Машиностроение», 1976, 184 с.
4. Методы классической и современной теории автоматического управления. Учебник в 3-х томах / Под ред. Н.Д. Егупова. — М.: Изд-во МГТУ им. Баумана, 2000.
5. Мирошник, И.В. Теория автоматического управления. Линейные системы (Серия: «Учебное пособие»). – СПб.: Питер, 2005. — 336 с.
6. Попов, Е.П., Бесекерский, В.А.,. Теория систем автоматического управления / Е.П. Попов, В.А. Бесекерский. – Изд. 4-е, перераб. и доп. – Спб.: Изд-во «Профессия», 2003. – 752 с.
7. http://habrahabr.ru/post/128704/
8. http://www.conf-ulstu.ru/nam_12.php

---

Количество просмотров публикации: Please wait

Все статьи автора «Michael»