Транспортный инфраструктурный комплекс является одним из наиболее значимых составных частей общего устройства экономической жизни городов и регионов. Транспортные сети многих населенных пунктов перегружены, поэтому особое значение приобретает их оптимальное планирование и оптимизация системы управления транспортным потоком. На помощь этому процессу приходит математическое моделирование транспортных сетей. Спектр применяемых при этом математических моделей и методов велик. Исходя из категории задач, на решение которых может быть направлено моделирование, выделяют следующие классы:
- Оптимизационные модели
- Имитационные модели
- Прогнозные модели
Если транспортная система населенного пункта хорошо изучена, т.е. известны ее размещение и основные характеристики, то для определения транспортных потоков можно использовать прогнозные модели, позволяющие рассчитать интенсивность потока, объемы перевозок в сети общественного транспорта по различным направлениям движения и т.д. Кроме того, данный класс моделей позволяет выполнить прогноз последствий изменений, происходящих в транспортной сети.
Дополнением к прогнозным моделям можно отнести имитационные модели, которые по своим результатам являются более детальными. При этом результат прогнозных моделей (усредненные значения потоков и их распределение) могут выступать входной информацией для имитационных моделей, описывающих более подробно не только процесс движения, но и развитие самого процесса во времени. К имитационным моделям можно отнести модели динамики транспортного потока. [1] Динамические модели более детально описывают движение транспортного потока: динамику скорости движения, задержки на перекрестках и другие характеристики движения. Поэтому для их реализации требуются достаточно мощные вычислительные средства.
Динамические модели включают в себя гидродинамические модели (описывают движение автомобилей в усредненных терминах), кинетические модели (описывают транспортный поток плотностью распределения его элементов в пространстве координат и скоростей единиц потока), микроскопические имитационные модели (описывают движение каждой единицы потока), модели типа клеточных автоматов (используется упрощенное дискретное во времени и пространстве описание движения элементов потока). [1, 25]. Остановимся на некоторых из них более подробно.
Гидродинамические модели: [2]
Транспортный поток при этом исследуется как поток одномерной сжимаемой жидкости, при этом учитывается, что поток сохраняется и существует взаимооднозначная зависимость между скоростью и плотностью потока. Кроме того допускается, что средняя скорость потока в каждый момент времени должна соответствовать равновесному значению при данной плотности автомобилей.
- Модели Гриншилдса и Гринберга
- Модель Гринберга:
- Модель Лайтхила-Уизема.
Предполагается:
- Транспортный поток непрерывен,
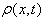– число автомобилей, занимающих единицу длины дороги. - Величина потока q(x,t) равная числу автомобилей, пересекающих черту х за единицу времени и определяется локальной плотностью .
Микроскопические модели [2]
- Модель следования за лидером (дифференциально-разностное уравнение):
Клеточные автоматы [2]
- Модель Нагеля-Шрекенберга:
Для оптимизации маршрутов транспортных перевозок, определения оптимальной структуры транспортной сети могут быть использованы оптимизационные модели.[3]
Библиографический список
- Швецов В.И. Математическое моделирование транспортных потоков. Автоматика и телемеханика. 2003, № 11. с.3-46
- Семенов В.В. Математическое моделирование динамики транспортных потоков мегаполиса. – Изд-во: Институт прикладной математики им. М.В. Келдыша, 2004.
- Морозов И.И. и др. Численное исследование транспортных потоков на основе гидродинамических моделей // Компьютерные исследования и моделирование 2011 Т.3№ 4 с.389-412
- Лившиц В.Н. Автоматизация планирования и управления транспортными системами. М.: Транспорт, 1987.
- Введение в математическое моделирование транспортных потоков: Учебное пособие / А.В.Гасников и др. – М.:МЦНМО, 2012. – 376с.
Количество просмотров публикации: Please wait