Введение.
В настоящее время становится ясно, что архитектура современных вычислительных систем, основанных на принципах Дж. фон Неймана имеет ряд существенных недостатков [1]. Последовательная организация вычислительного процесса предполагает относительно низкую производительность системы. Другой недостаток обусловливает низкую эффективность использования дорогостоящей памяти при наличии одного процессора-ядра. Это связано с тем, что подавляющее большинство ячеек памяти в процессе работы бездействует и поэтому коэффициент использования аппаратуры будет очень низким [2]. Третий недостаток – разработчик вынужден подстраивать алгоритм решения задачи под «жесткую» структуру вычислительной системы.
С другой стороны, инженерная реализация нейронного компьютера У. МакКаллока и У. Питтса , описанная в «Логическом исчислении идей, имманентных нервной активности» [2] в виде комплекса нейропроцессоров позволяет избавиться от перечисленных недостатков. Кроме того, преимуществом является то, что нейропроцессорные системы (НПС) различаются также по принципу взаимодействия структуры машины и решаемой задачи [2]. При использовании НПС уже разработчик подстраивает её структуру под решаемую задачу.
С появлением кластерных систем появилась проблема кластеризации вычислительных систем, т. е. эффективного разбиения на кластеры [1,2], что на практике решается не всегда оптимально или рационально. Такая же проблема видна и при использовании нейропроцессорных систем, преимуществом которых является высокая степень распараллеливания, близкая к 100% при решении определенных классов задач.
Цель работы - логическая организация и проектирование современных нейропроцессорных структур, на базе которых может появиться новый класс интеллектуальных систем [3]. Работа проводилась в рамках гранта РФФИ №14-07-00261 “Кластеризация и организация облачных и распределенных вычислительных систем на основе нейропроцессоров”.
Постановка задачи. Разработать фундаментальную методику организации и проектирования нейропроцессорной системы на основе кластеризации и анализа получаемых структур по различным техническим характеристикам.
Продукционная модель экспертной системы выбора НПС.
Предлагаемая модель выбора аппаратных и программных средств НПС базируется на функциональном принципе, согласно которому главную роль играет множество операций в отношении многопроцессорных структур [3].
На начальном этапе согласно функциональному принципу нейропроцессорная система рассматривается как взаимосвязанный набор устройств, реализованный на основе выбранной элементной базы, которая характеризуется: набором схем – чипсетов; набором команд; производительностью и стоимостью [4]. Эта задача зависит от множества факторов и рассматриваться не будет.
Проектируемая вычислительная структура НПС функционирует по некоторому алгоритму обработки и передачи информации 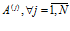 , который представляет собой кортеж операций
, который представляет собой кортеж операций 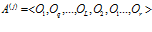 длиной
длиной 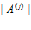
и, по сути, представляет собой множество искусственных нейронных сетей, запускаемых в нужном порядке. Тогда, с учетом задачи исследования, объектом теоретико-множественного анализа является вычислительная система на базе нейропроцессора для реализации алгоритма 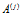 .
.
Тогда некоторый алгоритм 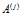 , реализующий множество нейронных сетей, представляет собой кортеж нейросетевых операций вида
, реализующий множество нейронных сетей, представляет собой кортеж нейросетевых операций вида 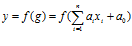 и операций управления. Введем множество операций
и операций управления. Введем множество операций 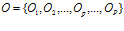 . С учетом введенного множества операций этот алгоритм нейросетевой обработки информации представляет собой кортеж операций
. С учетом введенного множества операций этот алгоритм нейросетевой обработки информации представляет собой кортеж операций 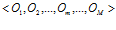 длиной
длиной 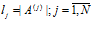 , где
, где 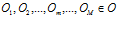 :
:
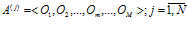 . (1)
. (1)
На этапе разработки программы каждой операции ставится в соответствие микрокоманда нейропроцессора 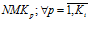 , то есть:
, то есть:
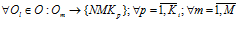 , (2)
, (2)
где 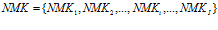 – множество нейромикрокоманд, написанных на внутреннем языке нейропроцессора;
– множество нейромикрокоманд, написанных на внутреннем языке нейропроцессора; 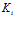 – минимальное количество нейромикрокоманд, необходимое для реализации некоторой операции
– минимальное количество нейромикрокоманд, необходимое для реализации некоторой операции 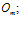
Далее, решая задачу (2), необходимо каждому 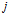 -му алгоритму нейрообработки
-му алгоритму нейрообработки 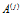 поставить в соответствие некоторую нейросетевую программу
поставить в соответствие некоторую нейросетевую программу 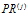 , то есть определить отношение:
, то есть определить отношение:
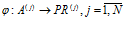 . (3)
. (3)
Таким образом, под программой 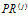 понимается кортеж нейромикрокоманд:
понимается кортеж нейромикрокоманд:
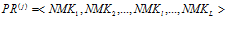 , (4)
, (4)
где 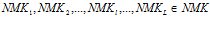 .
.
Далее производится разделение кода программы 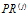
на множество подпрограмм 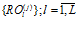 и загрузка подпрограмм на каждый нейропроцессорный модель (ПМ).
и загрузка подпрограмм на каждый нейропроцессорный модель (ПМ).
Математически данный этап можно описать следующим образом:
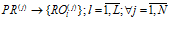 . (5)
. (5)
Введем понятие структуры 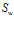 , под которым понимается отношение параллельности выполнения подпрограмм
, под которым понимается отношение параллельности выполнения подпрограмм 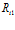 и
и 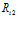 между соответствующими
между соответствующими 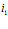 -м и
-м и 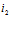 -м процессорными модулями, то есть
-м процессорными модулями, то есть 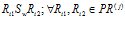 . Отношение параллельности понимается как выполнение одновременно двух или нескольких нейросетевых подпрограмм на разных, параллельно работающих нейропроцессорных модулях.
. Отношение параллельности понимается как выполнение одновременно двух или нескольких нейросетевых подпрограмм на разных, параллельно работающих нейропроцессорных модулях.
Тогда необходимо определить некоторую структуру 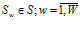 из множества всевозможных структур
из множества всевозможных структур 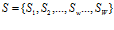 , позволившую некоторой
, позволившую некоторой 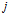 -й программе
-й программе 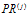 (4) поставить в соответствие множество подпрограмм нейросетевой обработки:
(4) поставить в соответствие множество подпрограмм нейросетевой обработки:
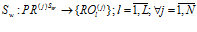 . (6)
. (6)
Введем понятие равенства подпрограмм нейросетевой обработки информации 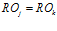 , под которым будет подразумеваться равенство их длин
, под которым будет подразумеваться равенство их длин 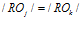 , под которым в свою очередь понимается равенство числа нейромикрокоманд подпрограмм, и совпадение подпрограмм с точностью до нейромикрокоманды
, под которым в свою очередь понимается равенство числа нейромикрокоманд подпрограмм, и совпадение подпрограмм с точностью до нейромикрокоманды 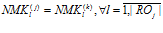 , т.е:
, т.е:
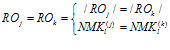 , (7)
, (7)
где 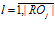 .
.
Рассмотрим отношение 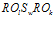 структуры
структуры 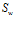 , которое указывает на то, что любые две произвольно взятые подпрограммы
, которое указывает на то, что любые две произвольно взятые подпрограммы 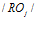 и
и 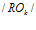 , удовлетворяющие (7), могут выполняться одновременно на разных ПМ, то есть:
, удовлетворяющие (7), могут выполняться одновременно на разных ПМ, то есть:
 . (8)
. (8)
Тогда справедливо утверждение о том, что отношение структуры обработки 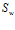 есть отношение эквивалентности [3].
есть отношение эквивалентности [3].
Введенное отношение структуры нейросетевой обработки позволяет разбить всю программу 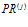 , определяемую согласно (4) на классы эквивалентности, т.е. классы неравных между собой нейросетевых подпрограмм согласно (5). Число классов эквивалентности обозначим через
, определяемую согласно (4) на классы эквивалентности, т.е. классы неравных между собой нейросетевых подпрограмм согласно (5). Число классов эквивалентности обозначим через 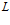 , а порядок класса
, а порядок класса 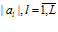 . Каждый класс эквивалентности имеет своего представителя в виде подпрограммы
. Каждый класс эквивалентности имеет своего представителя в виде подпрограммы 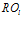 , имеющей число нейромикрокоманд равное порядку подпрограммы
, имеющей число нейромикрокоманд равное порядку подпрограммы 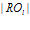 .
.
Таким образом, структура 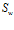 по определению ставит в соответствие некоторой
по определению ставит в соответствие некоторой 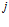 -й программе обработки информации
-й программе обработки информации 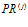
совокупность подпрограмм 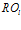 , число которых равно числу классов эквивалентности
, число которых равно числу классов эквивалентности 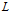 , а кратность
, а кратность 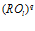 определяется порядком класса эквивалентности
определяется порядком класса эквивалентности 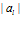 :
:
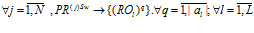 . (9)
. (9)
Если рассмотреть возможные структуры, полученные в результате решения задачи (9), то могут получиться структуры обработки: векторная, конвейерная, векторно-конвейерная, конвейерно-векторная,.
Если число классов эквивалентности 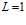 и порядок класса
и порядок класса 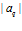 . Тогда
. Тогда 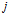 -му алгоритму нейросетевой обработки информации соответствует набор
-му алгоритму нейросетевой обработки информации соответствует набор 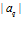 совершенно одинаковых подпрограмм. Если выходная информация каждой подпрограммы
совершенно одинаковых подпрограмм. Если выходная информация каждой подпрограммы 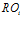 является входной для следующей
является входной для следующей 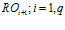 ; входная первой программы
; входная первой программы 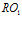 является входной, а последней
является входной, а последней 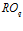 – выходной всего устройства, тогда назначая
– выходной всего устройства, тогда назначая 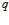 процессорных модулей на обработку информации, имеем конвейерную структуру НПС. Если входная информация требуется одновременно для всех подпрограмм, тогда назначая
процессорных модулей на обработку информации, имеем конвейерную структуру НПС. Если входная информация требуется одновременно для всех подпрограмм, тогда назначая 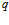 процессорных модулей на обработку информации, получаем векторную структуру НПС, в которой все
процессорных модулей на обработку информации, получаем векторную структуру НПС, в которой все 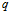 ПМ будут одновременно функционировать по одной и той же подпрограмме
ПМ будут одновременно функционировать по одной и той же подпрограмме 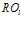 . Число ПМ в этом случае
. Число ПМ в этом случае 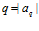 . Аналогичные рассуждения для случая, когда число классов эквивалентности равно
. Аналогичные рассуждения для случая, когда число классов эквивалентности равно 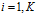 , порядок каждого класса равен
, порядок каждого класса равен 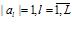 . Число ПМ в этом случае
. Число ПМ в этом случае 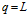 .
.
Объединим все подпрограммы, в которых информация передается параллельно, в 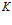
множеств. Тогда
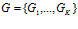 ,
, 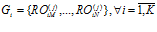 . Число подпрограмм в каждой группе различно для каждого множества
. Число подпрограмм в каждой группе различно для каждого множества 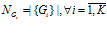 . Тогда, если все подпрограммы
. Тогда, если все подпрограммы 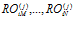 внутри множеств
внутри множеств 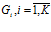 , обмениваются информацией последовательно, то структура является конвейерно-векторной и представляет собой структуру, в которой по принципу конвейера обрабатываются векторные потоки. Число ПМ будет равно
, обмениваются информацией последовательно, то структура является конвейерно-векторной и представляет собой структуру, в которой по принципу конвейера обрабатываются векторные потоки. Число ПМ будет равно 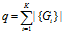 . Если в каждом множестве
. Если в каждом множестве 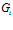 число подпрограмм равно 1, т.е.
число подпрограмм равно 1, т.е. 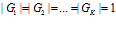 то имеем конвейерную структуру.
то имеем конвейерную структуру.
Объединим все подпрограммы, в которых информация передается последовательно, в 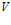
множеств. Тогда
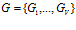 ,
, 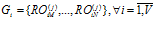 . Число подпрограмм в каждой группе различно для каждого множества
. Число подпрограмм в каждой группе различно для каждого множества 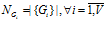 . Тогда, если всем подпрограммам
. Тогда, если всем подпрограммам 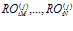 внутри множества
внутри множества 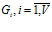 информация необходима одновременно, то структура является векторно-конвейерной и представляет собой структуру, в которой параллельно обрабатываются подпрограммы по принципу конвейера. Число ПМ будет равно
информация необходима одновременно, то структура является векторно-конвейерной и представляет собой структуру, в которой параллельно обрабатываются подпрограммы по принципу конвейера. Число ПМ будет равно 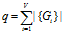 . Если в каждом множестве
. Если в каждом множестве 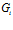 число подпрограмм равно 1, т.е.
число подпрограмм равно 1, т.е. 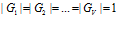 то имеем векторную структуру.
то имеем векторную структуру.
Экспертная система выбора НПС.
Нечеткий выбор структуры нейрокомпьютерной системы представляет собой сложный и трудоемкий процесс с большим объемом исходной информации. Поэтому для сокращения сроков проектирования таких систем была разработана экспертная система (ЭС) [1]. Исходными данными базы знаний являются характеристики алгоритмов: число классов эквивалентности 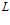 , порядок каждого класса
, порядок каждого класса 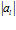 , механизм обмена данными между подпрограммами классов, входные и выходные данные, множество нейромикрокоманд для выбранного на первом этапе нейропроцессорного набора.
, механизм обмена данными между подпрограммами классов, входные и выходные данные, множество нейромикрокоманд для выбранного на первом этапе нейропроцессорного набора.
В качестве практических исследований была разработана программная подсистема “Конструктор нейропроцессорных систем” в разрабатываемой программной системе “NP-Studio” (рисунок 1).
Возможными элементами нейропроцессорной структуры могут быть: процессоры NM6403, NM6404, NM6405, NM6406, а также их эмуляторы. Также реализована возможность использования в одной нейпроцессорной системе реальных нейропроцессоров и одного эмулятора нейропроцессора той же модели.
Логическая организация вычислительной системы на базе нейропроцессоров реализуется за несколько этапов:
1. Выбор количества нейропроцессорных модулей.
2. Выбор структуры: конвейерная, векторная, конвейерно-векторная (несколько параллельных векторных потоков обрабатываются по принципу конвейера), векторно-конвейерная (параллельно обрабатываются несколько потоков, которые, в свою очередь, обрабатываются по принципу конвейера) или произвольная.
3. Если была выбрана произвольная структура, то необходим выбор активных связей между нейропроцессорными модулями.
4. Выбор используемого обеспечения (реальный нейропроцессор или эмулятор той же модели) для логического нейропроцессорного модуля.
После логической организации и проектирования нейропроцессорной системы, ее можно использовать для модулей контроля, управления и анализа программного комплекса NP-Studio”.
Важной особенностью разрабатываемого программного обеспечения является то, что реализована поддержка связей между распределенными вычислительными модулями системы, которые отличаются относительно медленной скоростью передачи информации. Также реализована поддержка нейропроцессорных модулей, работающих в облаке согласно принципам модели PaaS, IaaS. Такие модули отличаются тем, что доступ к ним реализуется посредством веб-сервисов различного назначения.
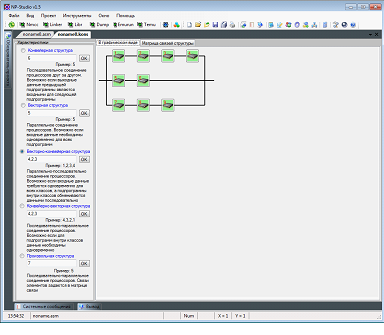
Рисунок 1 – Подсистема “Конструктор нейропроцессорных систем” в программной системе “NP-Studio”
Архитектура классов адаптирована для возможности добавления различных нейропроцессорных устройств. В основе диаграммы классов лежит следующая модель (рисунок 2).
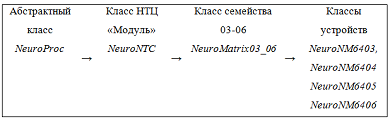
Рисунок 2 – Диграмма классов в программной системе “NP-Studio”
Добавление нового нейропроцессорного устройства реализовано специальными элементами управления в интерфейсе комплекса. Максимальное количество нейропроцессорных устройств на данный момент равно 10
Исходя из вводимых значений может быть получен тот или иной вид структуры, а также пользователем может быть реализован произвольный вид системы (рисунок 3).
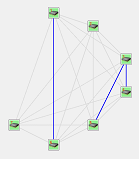
Рисунок 3 – Произвольная нейропроцессорная структура из семи процессорных модулей в программной системе “NP-Studio”
В случае выбора произвольной структуры может быть произведен экспертный анализ вида системы на основе описанного математического аппарата (рисунок 4).
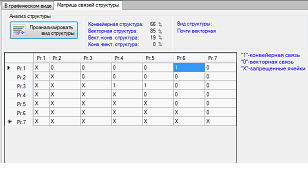
Рисунок 4 – Анализ нейропроцессорной структуры в программной системе “NP-Studio”
В качестве базы знаний была выбрана продукционная модель представления знаний, в которой связи между фактами представлены эвристическими правилами — выражениями декларативного знания об отношениях между объектами. Каждое такое правило имеет составляющую «ЕСЛИ» (предпосылка) и компонент «ТО» (заключение), которые определяют прямую и обратную причинно-следственную связь. Работа экспертной системы выбора нейропроцессорной структуры сводится к следующей последовательности действий.
-
Если число классов эквивалентности равно
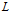 , И порядок каждого класса
, И порядок каждого класса 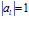 , И
, И
- обмен данными между подпрограммами в классах осуществляется последовательно, – ТО “конвейерная структура” (рисунок 5).;
- информация требуется одновременно всем подпрограммам классов, ТО – “векторная структура”
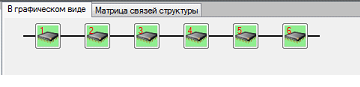
Рисунок 5 – Конвейерная нейропроцессорная структура из шести процессорных модулей в программной системе “NP-Studio”
Если в системе присутствуют распределенные связи, то есть нейропроцессорные модули удалены друг от друга, то в разработанной программной подсистеме линии между модулями выделяются пунктиром. В случае наличия облачного нейропроцессорного модуля, подключение к которому происходит через веб-сервис, он выделяется красным цветом (рисунок 6).
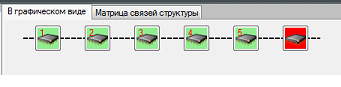
Рисунок 6 – Конвейерная нейропроцессорная структура из шести процессорных модулей с распределенными связями и облачным модулем в программной системе “NP-Studio”
-
Если число классов эквивалентности
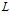 равно единице И порядок каждого класса
равно единице И порядок каждого класса 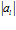 равен
равен 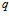 , И
, И
- обмен данными между подпрограммами в классах осуществляется последовательно, ТО – “конвейерная структура” (рисунок 7);
- информация требуется одновременно всем подпрограммам классов, ТО–”векторная структура”.
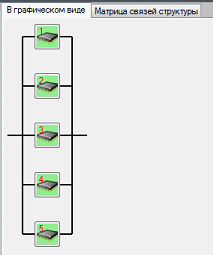
Рисунок 7 – Векторная нейропроцессорная структура из пяти процессорных модулей в программной системе “NP-Studio”
-
Если число классов эквивалентности
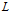 , И порядок каждого класса
, И порядок каждого класса 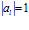 , И
, И
- обмен данными между подпрограммами в классах осуществляется последовательно, ТО – “конвейерная структура”;
- обмен данными между подпрограммами в классах осуществляется последовательно c небольшим исключением подпрограмм
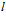 -го класса, ТО – “почти конвейерная структура”;
-го класса, ТО – “почти конвейерная структура”;
- обмен данными между подпрограммами в классах, кроме
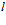 -го, осуществляется последовательно, а
-го, осуществляется последовательно, а 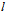 -му классу информация требуется одновременно, ТО – “конвейерно-векторная структура”;
-му классу информация требуется одновременно, ТО – “конвейерно-векторная структура”;
- подпрограммы обмениваются информацией последовательно, однако в некоторых классах информация требуется одновременно, ТО – “вроде конвейерно-векторная структура” (рисунок 8).
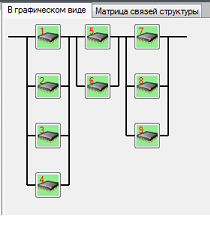
Рисунок 8 – Конвейерно-векторная нейропроцессорная структура из девяти процессорных модулей в программной системе “NP-Studio”
-
Если порядок каждого класса равен числу классов эквивалентности
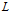 , ТО – “матричная структура”;
, ТО – “матричная структура”;
- информация сразу требуется подпрограммам всех классов, но в некоторых классах требуется последовательный обмен, ТО – “вроде векторно-конвейерная структура”;
- информация требуется одновременно подпрограммам всех классов, но подпрограммы
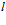 -го класса обмениваются последовательно, ТО – “векторно-конвейерная структура” (рисунок 9);
-го класса обмениваются последовательно, ТО – “векторно-конвейерная структура” (рисунок 9);
- информация требуется одновременно подпрограммам всех классов, кроме некоторых подпрограмм
 -го класса, ТО – “почти векторная структура”;
-го класса, ТО – “почти векторная структура”;
- информация требуется одновременно всем подпрограммам классов, ТО – “векторная структура”.
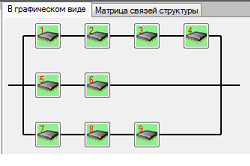
Рисунок 9 – Векторно-конвейерная нейропроцессорная структура из семи процессорных модулей в программной системе “NP-Studio”
Таким образом, ыыходными данными предложенной методики являются полученные в результате классификации структуры нейропроцессорной системы в виде нечетких переменныхв: конвейерная, почти-конвейерная, конвейерно-векторная, вроде конвейерно-векторная, матричная, вроде векторно-конвейерная, векторно-конвейерная, почти векторная, векторная.
Заключение.
В статье предложена обобщенная модель проектирования нейропроцессорной системы на основе нечеткой кластеризации. Разработана экспертная система анализа получаемых нечетких структур по различным техническим характеристикам согласно стратегии проектирования. Предложенная модель не зависит от конкретных алгоритмов и не определяет класс задач. Тогда как получение конкретной структуры НПС будет зависеть от алгоритмов, т.е. класса задач.
Библиографический список
- Злобин В.К., Ручкин В.Н., Нейросети и нейрокомпьютеры, СПб.: БХВ-Петербург, 2011, 256 с.
- Виксне П. Е., Фомин Д. В., Черников В. М. Однокристальный цифровой нейропроцессор с переменной разрядностью операндов //Известия ВУЗов. Приборостроение. – 1996. – №. 7. – С. 13-21.
- Романчук В.А., Ручкин В.Н. Алгоритмы анализа вычислительных структур на базе нейропроцессоров // Вестник Рязанского государственного радиотехнического университета. 2012. № 40. С. 60-66
- V. Ruchkin, V. Romanchuk, R. Sulitsa, “Clustering, Restorability and Designing Of Embedded Computer Systems Based On Neuroprocessors “, 2nd Mediterranean Conference on Embedded Computing MECO – 2013 Budva, Montenegro, 58-62 pp.
