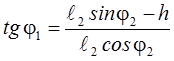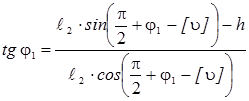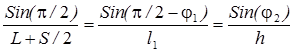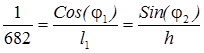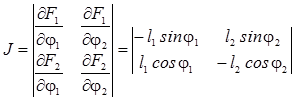Зона обслуживания погрузочного манипулятора является одной из важнейших характеристик погрузочного средства, чем больше площадь сечения зоны обслуживания в базовых плоскостях, тем меньше требуется глобальных перемещений манипулятора с грузом. Увеличение геометрической площади сечения зоны обслуживания погрузочного манипулятора возможно за счёт изменения длин исполнительных звеньев манипулятора, что в свою очередь ведёт к увеличению значений углов давления и усилий в исполнительных гидроцилиндрах, приводящих к повышенным энергозатратам на перемещение груза. Для расширения зоны обслуживания манипуляторов с поворотной стрелой можно использовать механизм поворота с тандемным (последовательным) включением исполнительных гидроцилиндров [1].

Угол поворота колонны зависит как от линейных размеров рычагов, так и от параметров исполнительных гидроцилиндров.

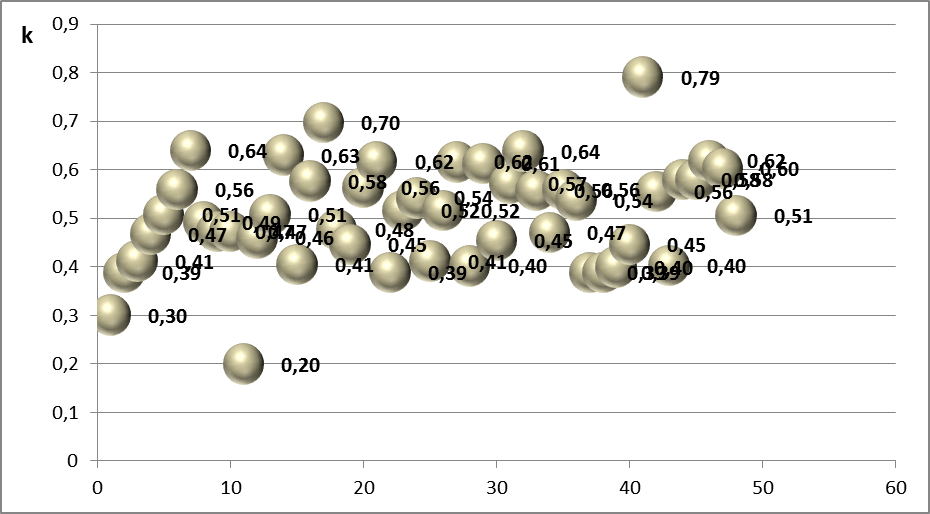Рисунок 1. Пузырьковая диаграмма распределения коэффициента удлинения цилиндров от количества анализируемых изделий.

Проанализировав номенклатуру гидроцилиндров, применяемых в сельскохозяйственном машиностроении, выявлено следующее: коэффициент удлинения (отношение хода штока к межосевому расстоянию) k=S/L колеблется от 0,2 до 0,8, причём наиболее часто используемые цилиндры имеют k=0,4…0,6 (рис.1 и 2).

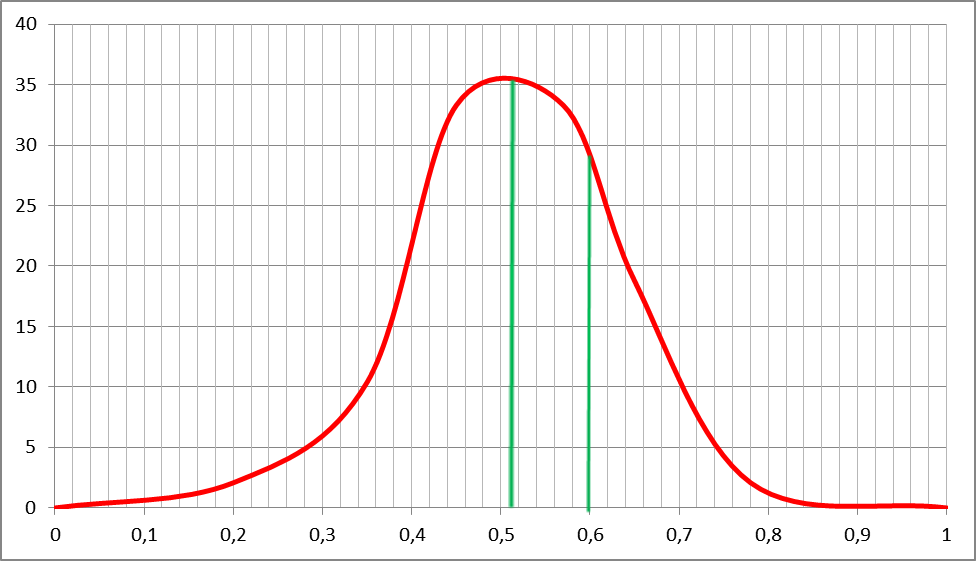Рисунок 2. Распределения гидроцилиндров по коэффициенту удлинения.

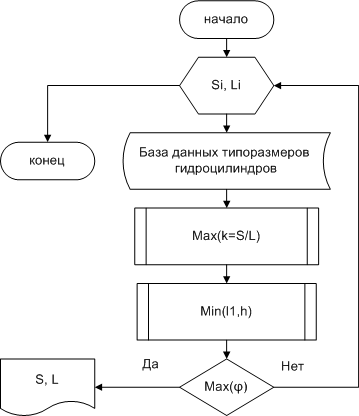Рисунок 3. Блок-схема программы подбора рациональных параметров гидроцилиндров механизма поворота.

Подбор наиболее рациональных параметров гидроцилиндра поворота колонны проводился на ЭВМ, блок-схема алгоритма выбора гидроцилиндра из базы данных типоразмеров приведена на рис. 3.

В качестве конкретного примера с учётом минимизации размеров механизма поворота выбираем гидроцилиндры с межосевым расстоянием менее 600 мм, например гидроцилиндр ЦГ-50.30х320.22 с межосевым расстояниеь L – 522 мм и ходом штока S, – 320 мм. Тогда коэффициент удлинения гидроцилиндра k=0,613, L_min=522 мм, L_max= 842 мм.

Оптимальные геометрические параметры (h, l₁, φ_min, φ_max) будем определять из уравнений проекции векторного контура с учётом углов давления [υ]≤60⁰ [2].

Составим уравнение векторного контура для одного гидроцилиндра (для второго контура задача будет решаться аналогично):

                                                (1)

Согласно рис. 4 уравнения проекций векторного контура

,                                         (2)

                                   (3)

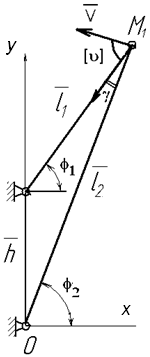Рисунок 4 –К определению уравнения векторного контура.

Разделив выражение (3) на (2), получим

.                                       (4)

Зададимся предельным углом давления [u], который в рычажных механизмах не должен превышать 60°. Найдя его взаимосвязь с j₁ (рис. 4), окончательно получим

.                                 (5)

Из выражения (5) определим j_1min и j_1max. Зная пределы изменения угла j₁, найдём множество координат точки М, получив угол поворота колонны со стрелой при заданном предельном угле давления в шарнирах [u].

Рассмотрим частный случай положения механизма поворота, когда угол φ₁=0. В этом случае будем считать, что l₂=L+S/2, тогда по теореме синусов при β=π/2-φ2 (рис.5)

                         (6)

Рисунок 5 – К определению зависимостей h и l₁ от углов поворота звеньев.

Из выражения (6) при Sin(π/2)=1 и L+S/2=686 мм следует

                                  (7).

Тогда при φ₁=0 h=682·Sin(φ₂) и l₁=682·Cos(φ₂), где 30⁰< φ₂<60⁰, так как γ= φ₂=π/2-[υ].

На рис. 6 представлен график изменения h и l₁ от φ₂, на основании которого принимаем значения h и l₁, удовлетворяющие допускаемым углам давления. Перед тем как принять по графику (рис.6) значения h и l₁, определим, занимает ли механизм поворота особые положения, геометрически вырождающие механизм.

Неассуровая структурная группа –кинематическая цепь с ненулевым числом независимых входов, равных числу степеней подвижности. Такие группы используют в исполнительных механизмах подъемно-транспортных и строительно-дорожных машинах, роботах и манипуляторах. Для нахождения особых положения необходимо ввести дополнительные обобщенные координаты и составить функцию положения механизма, а затем найти якобиан для данного механизма. Признак особых положений – это равенство якобиана нулю. Из этого условия и находятся значения дополнительных обобщенных координат, соответствующих особым положениям.

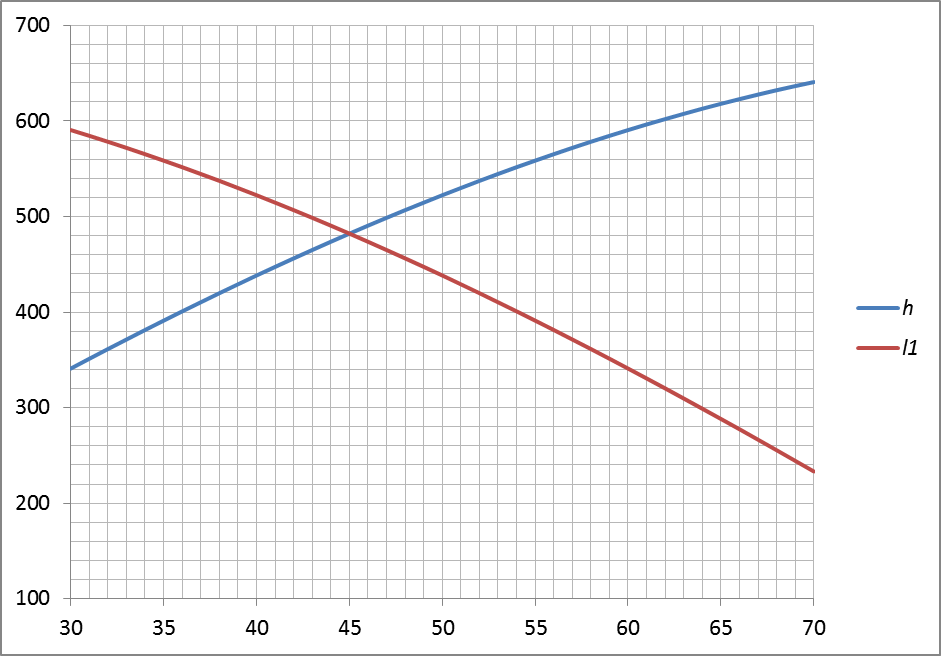Рисунок 6 – График изменения h и l₁ от φ₂

          Для механизма, представленного на рис.4 функциями положения будут выражения (2) и (3), тогда якобиан примет вид:

                         (8)

         Вырождение для особого положения:

                           (9)

Из выражения (9) видно, что особые положения наблюдаются при φ₁=0 и φ₂=0, или при φ₁=π/2 и φ₂= π/2. Для рассматриваемого механизма эти значения углы поворота звеньев не принимают.

Геометрический признак особых положений, это расположение шарнира М на оси шарниров ОО₁.

Принимаем h=602 мм, l₁=300 мм (немного уменьшенное значение). Для принятых значений используя выражения (2) и (3) определим зависимости изменений угла поворота рычага l₁ при изменении длины гидроцилиндра от l_2min=522 мм до l_2max=842 мм (рис.7).

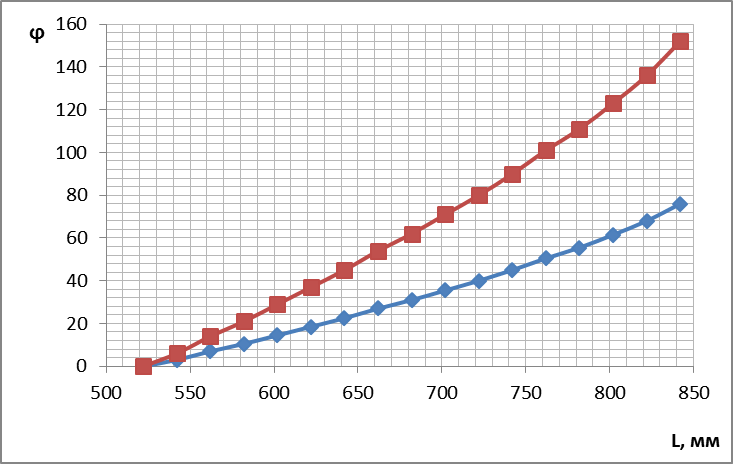Рисунок 7 – Зависимость угла поворота рычага поворотной колонны от одновременного удлинения цилиндров.

         Полученные зависимости  изменения угла  φ₁ нелинейны, в итоге получим нелинейные законы изменения  скоростей и ускорений.

Основные преимущества предлагаемой схемы привода поворотной стрелы погрузчика:

1. При зоне действия рабочего органа в горизонтальной плоскости 75^о, поворот стрелы дополнительным цилиндром расширяет зону до 150^о. Угол поворота стрелы естественно зависит от хода поршня цилиндра.
2. Поворот стрелы может происходить при угловой скорости, почти в два раза превышающую скорость одной из составных частей колонны, т.к. угловые скорости складываются. Асинхронной работой обоих цилиндров можно добиться более медленного поворота, а в нужный момент времени плавно останавливать стрелу.

1. Патент РФ №2455222. Гидропривод погрузчика с поворотной колонной. Несмиянов И.А., Герасун В.М., Воробьева Н.С., Токарев В.И., Турыгин П.В. Опубл. 10.07.2012. Бюл.№19.
2. В М. Герасун, В.И.Пындак, И.А.Несмиянов, В.В.Дяшкин-Титов, В.Е.Павловский. Манипуляторы для мобильных роботов. Концепции и принципы проектирования // Препринт ИПМ им. М.В.Келдыша. 2012. №44. 24 с. URL://library.keldysh.ru/preprint.asp?id=2012-44.

Все статьи автора «Несмиянов Иван Алексеевич»