В задачах сейсмики сооружений [1,2,3,4,5], ветровых колебаний [6,7], или в физически нелинейных задачах при учете истории нагружения [8, 9,10] необходимо отслеживать состояние системы с оценкой устойчивости. При этом, данная вспомогательная задача должна достаточно просто решаться. 
Для характеристики величины изменения амплитуд с ростом нагрузки необходимо ввести некоторую норму этого отклонения. Эту норму целесообразно сделать зависимой от приращения нагрузки, т. е. нормировать . При этом необходимо отслеживать, какую кривизну кривой равновесных состояний создают два последовательных отношения приращений и исходная амплитудная точка.
Самым эффективным и общим методом анализа произвольных систем дифференциальных уравнений, описывающих НДС конструкции, является метод пошагового анализа уравнений равновесия. Именно эту методику удобно использовать при анализе устойчивости напряжённо-деформированного состояния по кривой равновесных состояний системы. При этом собственно для анализа устойчивости достаточно сопоставить результаты расчётов двух шагов – начального и конечного. 
Пусть действующая на конструкцию нагрузка. - возможное приращение нагрузки, составляющее малую определённую часть от (например, 0.05). - начальное обобщённое перемещение системы, соответствующее полной нагрузке, равной . Если при стыковочном анализе начального и текущего участков кривой (рис.1) имеется весьма существенное отклонение от начальной прямой – процесс деформирования неустойчив. Для исследования устойчивости данного равновесного состояния можно сделать малое положительное  приращение нагрузки и оценить приращение обобщённого перемещения . Пусть норма сеточной функции  есть неотрицательное число, которое принимается за меру отклонения линии ВС от прямолинейной зависимости -. Здесь точки В и С имеют координаты  и , соответственно.

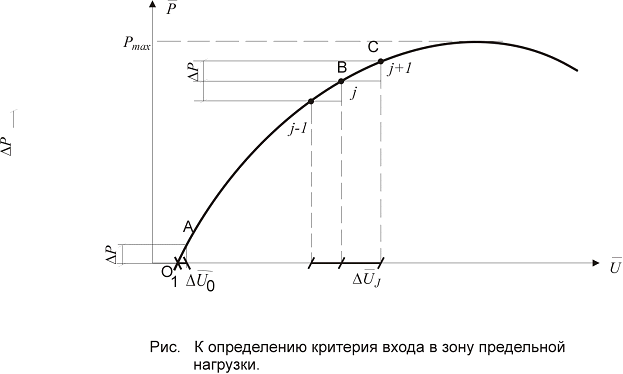
Рис. 1. К определению критерия входа в зону предельной нагрузки

Определим методику вычисления этой нормы. Если при одинаковых приращениях нагрузки имеются одинаковые приращения перемещений, то имеет место линейная связь Р – U. Мягкое снижение жесткости соответствует отношению
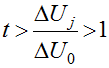, (1)
где t – некоторое предельное число, принимаемое за критерий входа в зону слабой устойчивости, например t=2 . 
Как известно, теория устойчивости по Ляпунову утверждает, что если система находится в состоянии устойчивого движения, то в ответ на малые возмущения следуют малые отклонения. Аналогичный, по сути, подход применяется и здесь: если на исследуемом участке движения (равновесия) малые возмущения нагрузки вызывают малые изменения напряжённо-деформированного состояния – система устойчива.
Определимся с термином «малое изменение напряжённо-деформированного состояния».
Если диаграмма Р – U имеет вид плавной кривой с ниспадающей ветвью, то всегда можно найти  такое, что на одной из ступеней нагружения будет 
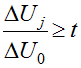. (2)
Итак, если норма сеточной функции  достигла или превысила значение t , то конструкция исчерпала заданный показатель устойчивости.
Величина t, очевидно, связана с начальной жёсткостью системы. Поэтому для гибких тонкостенных систем достаточно принять t=2. Для достаточно жёстких систем можно принять t=3. 
Сближение концов k-го стержня
 (3) 
где i – номер сечения стержня.
Обобщенное перемещение системы 
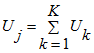, (4) 
где K- количество стержней системы. 
Величина, определяемая по соотношению , покажет нам состояние системы.

1. Шеин А.И. Метод сеточной аппроксимации элементов в задачах строительной механики нелинейных стержневых систем // М-во образования и науки Рос. Федерации, Федер. агентство по образованию, Пенз. гос. ун-т арх. и стр-ва. – Пенза, – 2005. – 248 стр.
2. Шеин, А.И. Решение многопараметрической задачи динамики стержневых систем методом сеточной аппроксимации элементов //Промышленное и гражданское строительство. – 2002. – № 2. – С.- 27.
3. Шеин, А.И. Оценка эффективности активного жидкостного гасителя колебаний высотных сооружений при нестационарных воздействиях/ А.И. Шеин, Д.А. Шмелев // Строительная механика и расчет сооружений. – 2014. – №1(252). – С. 59-63.
4. Шеин, А.И. Гашение колебаний высотных сооружений в 3 ч. / А. И. Шеин [и др.] // М-во образования и науки Российской Федерации, Гос. образовательное учреждение высш. проф. образования “Пензенский гос. ун-т архитектуры и стр-ва”.-  Пенза, – 2011
5. Шеин, А.И. Метод смещенных разностей для решения систем дифференциальных уравнений движения механических систем / А.И. Шеин, М.Б. Зайцев // Строительная механика и расчет сооружений. – 2012.- №2. –  С. 38-41.
6. Шеин, А.И. Схемы и теория гасителей пространственных колебаний сооружений / А.И. Шеин, О.Г. Земцова//  Региональная архитектура и строительство. -2010. – №1. –  С. 45-52.
7. Шеин, А.И. Снижение уровня колебаний системы “упругое основание – высотное сооружение” с помощью нелинейного динамического гасителя / А.И. Шеин, О.Г. Земцова //. Региональная архитектура и строительство.- 2011.- № 2.- С. 83-90.
8. Завьялова, О.Б. Применение условного сдвиго-изгибного стержня при расчете рам на устойчивость / О.Б. Завьялова, А.И. Шеин .//Известия высших учебных заведений. Строительство. -2010.- №1.  С. 99-105.
9. Шеин, А.И. Влияние физической нелинейности бетона на напряженно-деформированное состояние элементов монолитных железобетонных рам, рассчитываемых с учетом истории нагружения / А. И. Шеин, О.Б. Завьялова// Промышленное и гражданское строительство. – 2012.- №8.- С. 29-31.
10. Шеин, А.И. Расчет монолитных железобетонных каркасов с учетом последовательности возведения, физической нелинейности и ползучести бетона/ А. И. Шеин, О.Б. Завьялова // Строительная механика и расчет сооружений. 2012. № 5. С. 64-69.

Все статьи автора «Ладин Роман Акбарович»