Существует множество задач, исходные данные, для решения которых являются нечеткими. Для решения этих задач часто применяют нечеткие множества [2]. Предлагаемая модификация проективной геометрии учитывает представление информации, с одной стороны, как случайных величин, подчиненных нормальному закону распределения ошибок, с другой стороны, как нечетких множеств [4, 7]. 
В данной статье прямую рассмотрим в двумерной модели нечеткой проективной геометрии.
Существует только одна нечеткая двухмерная прямая принадлежная паре нечетких двухмерных точек [6].
Пусть даны две принадлежные прямой нечеткие двумерные точки [5]  и  (рис.1). Выберем начало новой системы координат  в точке , ось  проведем через ,. Спроецируем нечеткие двумерные точки на прямые, проходящие через математические ожидания точек  и . и перпендикулярные прямой , их соединяющей. Получим две нечеткие одномерные точки  и [8].
Нечеткая двумерная прямая  принадлежна паре нечетких двухмерных точек  и  есть область возможных положений прямых случайным образом пересекающих нечеткие одномерные точки  и . Любое сечение прямой  перпендикулярное , является одномерной точкой . Определим характер распределения этих точек и закономерности, связывающие их параметры с базовыми точками  и . 
Пересечем  и  произвольной прямой  (рис. 2). На расстоянии  от начала координат выберем точку . Величины  и  подчинены нормальному закону распределения. Величину 
 характеризующую распределение точки  можно подсчитать следующим образом
, , ,
, , (1)
.

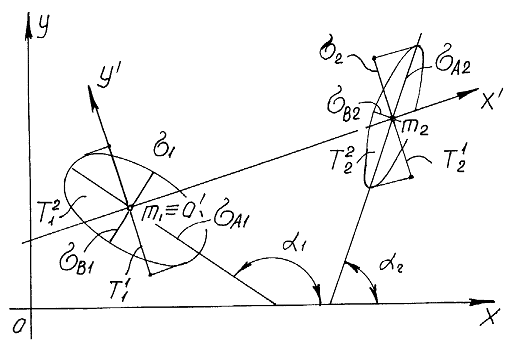
Рис.1 Две непринадлежные двухмерные нечеткие точки ,  и их проекции , .

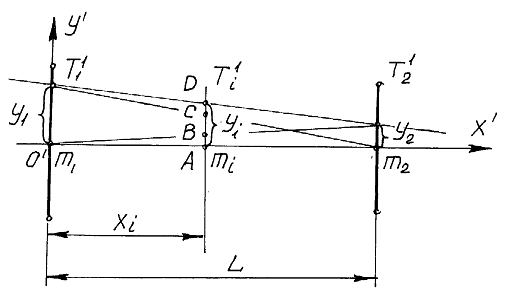
Рис. 2 Определение параметров распределения произвольной одномерной точки (сечения прямой).
Величина  представляет собой линейную функцию величин  и , подчиненных нормальному закону, следовательно, она сама подчинена нормальному закону распределения [1]. Найдем параметры величины  математическое ожидание и среднее квадратичное отклонение.
, (2)
 (3)
где  - коэффициент корреляции величин  и , в нашем случае он равен 0, так как величины независимые, некоррелированы.
 (4)
Подставим = и выясним зависимость изменения среднего квадратичного отклонения от x.
 (5)
где , , ,
Геометрическим местом точек изображающих  является гипербола, на мнимой оси которой лежат математические ожидания . Асимптоты этой гиперболы (рис. 3) являются изображением средних квадратичных отклонений нечеткой несобственной точки  прямой , нечеткая одномерная точка с минимальным  вписывается в центр кривой (точка m) и имеет параметры 
,
где ,  
Определим закон распределения прямой. Выберем оси координат (рис. 4), начало в центре, а ось  на мнимой оси гиперболы. Представим случайную прямую уравнением
, (6)
где ,  - отрезок ОВ
Крайнее положение прямой проходящей через точку В – касательная к гиперболе в точке .
Уравнение касательной 
, (7)

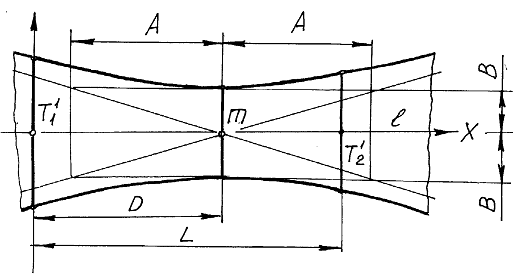
Рис. 3. Центр и бесконечно удаленная точка нечеткой прямой.

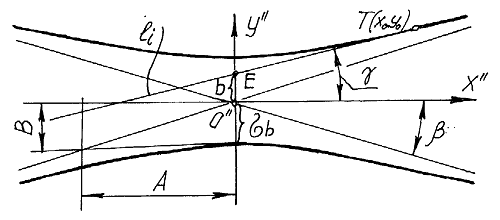
Рис. 4 Определение закона распределения параметров прямой.

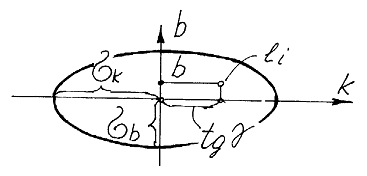
Рис. 5 Эллипс рассеивания параметров нечеткой прямой.

Преобразуем уравнение (7) к виду (6)
, (8)
где , , (9)
Величины  и  связаны уравнением 
, (10)
из уравнения (10) найдем  из (8) найдем  и подставим их в уравнение (8) полученное уравнение преобразуем к каноническому виду
, (11) 
, (12)
Уравнение (12) – уравнение эллипса. Параметр  подчинен нормальному закону (отклонение от математического ожидания центральной точки прямой),  среднее квадратичное отклонение той же точки,  можно интерпретировать как отклонение от математического ожидания в несобственной точке прямой, а  ее среднее квадратичное отклонение. Нечеткая двумерная прямая представлена в виде двойственного ей объекта нечеткой двумерной точки (рис. 5) в системе координат . Каждая случайная прямая изображается точкой на плоскости. Нечеткая двумерная прямая это система двух нормально распределенных случайных величин 
. (13)
Таким образом, нечеткая прямая задана двумя стандартными точками, центральной и несобственной. 
Стандартное задание нечеткой двумерной прямой будет определяться пятью параметрами 
где m (m_x, m_y) – центр прямой, математическое ожидание центральной точки прямой,
 - среднее квадратичное отклонение центральной точки,
 - среднее квадратичное отклонение несобственной точки прямой,
 - угол наклона прямой, направление на несобственную точку прямой.
Одновременно все эти параметры являются параметрами гиперболы изображающей на плоскости нечеткую прямую (рис. 6). Ветви гиперболы ограничивают область, где прямая может появляться с заданной вероятностью.

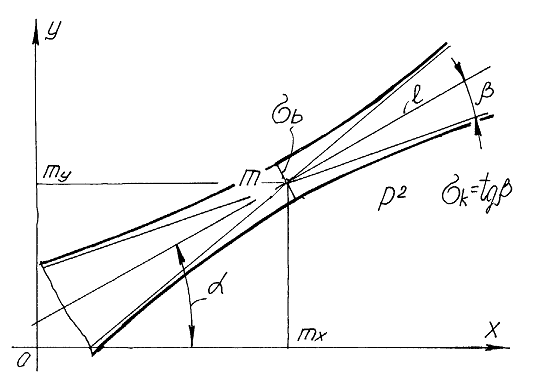
Рис. 6 Собственная двухмерная нечеткая прямая.

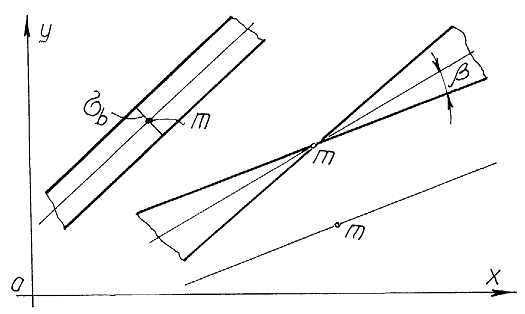
Рис. 7 Частные случаи собственной нечеткой прямой.

Несобственная ось гиперболы прямая Р - математическим ожиданием нечеткой двумерной прямой. Прямые касательные к гиперболе являются изображениями сигма прямых аналогов точек принадлежащих сигма эллипсу нечеткой двумерной точки. На рис. 7 изображены частые случаи нечеткой двухмерной прямой: а) = 0, б) = 0, в) == 0
Нечеткие прямые на плоскости могут быть собственными и несобственными. Каждая проективная плоскость содержит одну нечеткую несобственную прямую . Она проходит через две несобственные точки. Ее математическое ожидание – несобственная прямая проективной плоскости. Гипербола, изображающая несобственную прямую выродилась в окружность с радиусом  - достаточно большое наперед заданное число. 
Нечеткой прямой с параметрами  на плоскости, будем называть подмножество  такое, что
  (14)
Подмножество  также называется нечетким подмножеством, соответствующим нечеткой точке с параметрами 
Легко установить, что функция принадлежности изменяется в интервале [0,1] и ставит в соответствие каждому элементу  число  из интервала [0,1]. Точками перехода, то есть значениями  для которых , являются точки гиперболы с параметрами
 ,
высота нечеткого множества

На основе нечеткой проективной геометрии был разработан ряд алгоритмов предназначенных для геометрического моделирования утраченных памятников архитектуры [3]. Разработаны одномерный и двухмерный варианты алгоритмов. Каждый алгоритм состоит из отдельных задач. Для их решения написан на языке AutoLisp в среде AutoCAD комплекс программ, реализующий операции нечеткой проективной геометрии. В следующей статье будут рассмотрены случаи пересечения и параллельности нечетких прямых.
Работа выполнена в рамках Программы стратегического развития ПетрГУ на 2012-2016 гг.

1. Вентцель Е.С. Теория вероятностей: Учеб. для вузов. – 6-е изд. стер. – М.: Высш. шк., 1999. – 576 c.
2. Воронова А.М., Воронов Р.В. Обоснование использования нечетких структур для моделирования размещения погрузочных пунктов и сети волоков на лесосеке // Актуальные вопросы современной науки. 2009. № 7-1. С. 86-93.
3. Косенков А.Ю., Марков Б.Г., Марков О.Б. Графическая реконструкция часовни иконы смоленской божьей матери в деревне Кинерма // CARELiCA. 2013. Т. 1. № 1-1 (10). С. 155-162.
4. Марков Б.Г. Автоматизация геометрического моделирования утраченных памятников архитектуры по иконографическим материалам //  диссертация на соискание ученой степени кандидата технических наук / Петрозаводск, 2000.
5. Марков Б.Г., Марков О.Б. Геометрическая интерпретация нечеткой точки  //  депонированная рукопись  № 1402-В2003 16.07.2003.
6. Марков Б.Г., Марков О.Б. Геометрическая интерпретация нечеткой прямой  //  депонированная рукопись  № 1401-В2003 16.07.2003.
7. Марков Б.Г., Марков О.Б., Борисов А.Ю. Особенности геометрического моделирования утраченных памятников архитектуры // Ученые записки Петрозаводского государственного университета. Серия: Естественные и технические науки. 2013. № 8 (137). С. 88-92.
8. Марков Б.Г., Марков О.Б., Воронов Р.В. Модель одномерного нечеткого проективного пространства // Современные проблемы науки и образования. 2013. № 6. С. 894.

Все статьи автора «Марков Борис Георгиевич»