Одним из направлений математического моделирования является использование информационных компьютерных технологий для решения прикладной научно-технической задачи [1…6]. С методологической точки зрения моделирование есть метод научного познания. При замене реального объекта или процесса его формальным описанием (формализация) исследователем отбрасываются несущественные для изучения объекта характеристики. Выбор характеристик объекта-оригинала, которые при этом сохраняются и войдут в модель, определяется целями моделирования. Основное требование, предъявляемое к моделям, состоит в адекватном описании реальных процессов или объектов, которые замещает модель. В математической модели существенные черты объекта или процесса определяются на языке уравнений или других математических средств. Компьютерное моделирование состоит из серии вычислительных экспериментов для анализа, интерпретации и сопоставления результатов моделирования с реальным поведением изучаемого объекта а, при необходимости, последующего уточнения модели. При математическом моделировании не всегда требуется компьютерная поддержка. Более того, всегда отдается предпочтение аналитическим методам исследования модели перед численными методами. К сожалению, практическая реализация аналитических методов часто сопряжена с большими трудностями, что и приводит к необходимости использования численных методов и компьютерного моделирования. Аналитические методы и компьютерное моделирование не только не противостоят друг другу, но их взаимное проникновение способствует лучшему пониманию исследуемых процессов в динамике (например, системы визуализации). Все это и определяет компьютерное моделирование как один из основных методов познания в научных и практических исследованиях. Ограничимся некоторыми приложениями указанных методов к разработке композиционных материалов специального назначения с заранее заданными свойствами. Экспериментальное определение их свойств требует проведения большого объема дорогостоящих исследований; налицо необходимость построения теоретических моделей для определения усредненных значений параметров материалов и описания процессов формирования их физико-механических характеристик. Так, математическая модель, описывающая поведение неоднородной композиционной среды, включает ряд уравнений с быстро меняющимися коэффициентами, которые характеризуют свойства отдельных компонентов материала. К сожалению, ее использование требует решения краевых задач (возникают большие трудности даже при использовании современных вычислительных комплексов). Нужны модели, сводящиеся к более простым уравнениям с некоторыми усредненными коэффициентами. Естественно, решение соответствующей краевой задачи должно быть близким к решению исходной. 
Известны немногочисленные попытки получения аналитических зависимостей для определения свойств компонентов композиционных материалов и их концентрации в смеси со свойствами готового композита.Такие зависимости принципиально позволяют определить и концентрацию, и гранулометрические характеристики ингредиентов материала в зависимости от предъявляемых к нему требований; известна методика определения критической концентрации (зависимость критической объёмной концентрации от среднего значения гранулометрического состава заполнителя). Методами математического моделирования и оптимизации определяется эффективная прочность композитных материалов (некоторая усреднённая прочность материала в целом). Здесь же предлагается программа, позволяющая определить концентрацию, гранулометрический состав заполнителя и желаемую прочность материала, исходя из прочности чистого вяжущего, диапазона разброса гранулометрического состава заполнителя и значения желаемой прочности композита.Перспективность компьютерного материаловедения для создания композитных материалов с высокими эксплутационными свойствами, долговечностью и надежностью очевидна Это и изучение процессов формирования структуры композитных материалов, и влияние характера распределения заполнителя на свойства материалов. Возможно изучение теплопроводности, электропроводности и диэлектрических свойств композитов. Известны и работы по изучению процесса возникновения дефектов в композитных материалах (трещины, поры, раковины и т. п.) и оптимизации составов композитов (исходя из минимума трещинообразования, заданной пористости и др.).
В настоящее время при синтезе композиционных материалов используется некий симбиоз аналитических методов и компьютерного моделирования. С учетом собственного опыта и опыта работы других авторов по синтезу композитов можно рекомендовать методику, включающую:
- моделирование отдельных свойств;
-определение параметров для характеристики моделей;
- установление связей параметров моделей от рецептурно-технологических характеристик;
- определение зависимостей свойств от рецептурно-технологических параметров (метапараметров ; функции параметров модели);
- ранжирование свойств материалов;
- определение множества частных критериев;
- минимизацию размерности критериального пространства;
- многокритериальную оптимизацию качества материала с определением оптимальных рецептурно-технологических параметров.
Свойства определяются как интегральные характеристики многофазного материала (состоит из двух и более компонент; между компонентами существуют границы раздела; один из компонентов – матрица (связующее) – связным образом заполняет пространство; другие компоненты (включения) занимают изолированные области) в зависимости от параметров матрицы (связующего), размеров включений и расстояний между ними. Обычно размеры включений и расстояния между ними по сравнению с молекулярными можно считать достаточно большими, но по сравнению с характерными размерами материала – малыми ( однородность композита в макроскопическом масштабе (размеры рассматриваемого тела) и неоднородность в микроскопическом; дисперсный (гранулированный) композит состоит из включений (зерен) со всеми одинаковыми размерами).
Разработана подробная методика определения свойств композитов через параметры кинетических процессов формирования эксплуатационных характеристик. 
Несмотря на определенные трудности в интерпретации многофакторных экспериментально-статистических моделей свойств материалов, нельзя недооценивать их роль при составлении когнитивной карты, ранжировке частных критериев и оптимизации (в том числе векторной) характеристик материала. 
Ценность разработанной модели определяется тем, насколько правильно она описывает процессы и зависимости в композите, как в сложной системе; пределы применимости модели определяются гипотезами, лежащими в ее основе.
Перспективным является построение таких теоретических моделей композиционных материалов, которые позволят определять их осредненные характеристики с описанием локальных особенностей.
Свойства исследуются c использованием одной или нескольких узко-ориентированных моделей; наращивание множества упрощенных моделей производится по мере необходимости. В частности, при синтезе серных композиционных материалов частные критерии выбираются исходя из технического задания. Основными моделями являются аналитические зависимости, определенные на основе экспериментальных данных и используемые для описания отдельных свойств. 
Так, модель подвижности смеси [7] используется для описания структурных преобразований в композите, оказывающих существенное влияние на подвижность смеси в зависимости отношения от степени наполнения:

.

(1)

Что касается прочности композиционных материалов от степени наполнения ,то чем больше дисперсность наполнителя (не зависит от химической активности), тем при меньшей степени наполнения достигается максимальная прочность материала. Если в композите отсутствуют структурные преобразования,то влияние границы раздела фаз «дисперсная фаза – вяжущее вещество» минимально. Зависимость свойств композита от содержания дисперсной фазы подчиняется правилу смесей (закон аддитивности). Вовлекаемый воздух является дополнительной дисперсной фазой. В ряде случаев прочность увеличивается при значениях, не превосходящих , или происходят качественные структурные преобразования: образование разветвлённого граничного слоя вяжущего, имеющего повышенные показатели свойств.
Прочность зависит от структуры и фазового состава (наполнитель (дисперсная фаза твёрдых частиц), вяжущее (матрица), воздушные поры (дисперсная фаза воздушных включений)):

; = , + = .

В общем случае восходящая ветвь зависимости  от характеристик и содержания наполнителя имеет вид:

= ; (2′)
;  ;

При степенях наполнения, превосходящих , наблюдается постепенное уменьшение прочности композита. Прочность на нисходящей ветви  определяется в виде:

,

(2”)

.
В серных материалах пористость  определяется уменьшением объёма (на 14,1%) серы при переходе из жидкого состояния в твёрдое. В процессе изготовления композитов сера частично взаимодействует с наполнителем с образованием сульфидов и газообразного диоксида серы, что также способствует возникновению пор.
Для пористости на границе раздела фаз справедливо

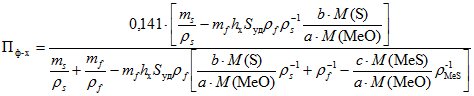
с введением наполнителя уменьшается. 
При  пористость серного материала возрастает (дефицит вяжущего приводит к образованию в серном материале агрегатов из не смоченных частиц наполнителя), а именно:

.

(3)

Для радиационно-защитных композитов важно получение модели радиационного разогрева при ионизирующем излучении. Достаточно подробно этот вопрос рассматривается в [7,8]. В частности модель имеет вид :

; ,

(4)

если температурное поле – равномерное; толщина h конструкции – постоянна (стационарный режим – при ).

1. Гарькина И.А., Данилов А.М., Смирнов В.А. Флокуляция в дисперсных системах / Системы управления и информационные технологии. – 2008.  – № 2.3(32).  – С.344-347.
2. Гарькина И.А., Данилов А.М., Сорокин Д.С. Синтез композиционных материалов с позиций классической теории оптимального управления /Фундаментальные исследования.- 2014. - № 9-7. – С. 1411-1416.
3. Гарькина И.А., Данилов А.М., Королев Е.В. Когнитивное моделирование сложных слабоструктурированных систем: пример реализации / Региональная архитектура и строительство. – 2008. - № 2.-  С. 16-21.
4. Будылина Е.А., Гарькина И.А., Данилов А.М., Сорокин Д.С. Синтез композитов: логико-методологические модели // Современные проблемы науки и образования. – 2014. – № 5; URL:http://www.science-education.ru/119-14283
5. Данилов А.М., Гарькина И.А., Смирнов В.А., Королева О.В. Математические методы при разработке и управлении качеством материалов специального назначения / Строительные материалы.  –  2010. – №3. –  C.112-117.
6. Гарькина И.А. Формализация оценки структуры и свойств композиционных материалов специального назначения / Строительные материалы. – 2007.– № 1. – С. 70-72.
7. Альбакасов А.И., Гарькина И.А., Данилов А.М., Королев Е.В. Оптимизация систем со сложной иерархией / Вестник гражданских инженеров. – 2012. -№ 2. – С. 324-327.
8. Альбакасов А.И., Гарькина И.А., Данилов А.М., Королев Е.В. Управление структурой и свойствами наномодифицированных строительных материалов / Региональная архитектура и строительство. – 2011. – № 2.  – С. 9-17.

Все статьи автора «fmatem»