Знание положения главных центральных осей сечения стержня играет решающую роль при его расчете на прочность, жесткость и устойчивость по формулам сопротивления материалов. Особую роль данное положение занимает для тонкостенных стержней.
В данной работе рассматривается задача определения положения главных центральных осей для Z-образного тонкостенного профиля при различных соотношениях длины полки к длине стенки.
Постановка задачи:
при каком  где – полная длина Z-образного профиля, оси XY являются главными центральными осями сечения, т.е. найти угол α.
Принять толщину (рис.1)

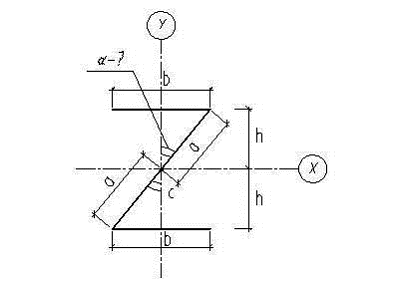
Рис.1

Т.к. данная форма сечения имеет центральную симметрию (т. С, рис.1), то центр тяжести сечения будет совпадать с центром симметрии. Следовательно, все оси, проходящие через центр тяжести (т.С, рис.1), являются центральными осями.
Оси XY являются главными осями, если центробежный момент инерции сечения равен нулю, т.е.

Предварительно определяем диапазон изменения 
При  или b = 0 имеем рис.2, а при или имеем рис.3

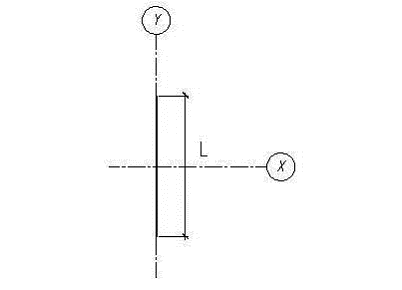
Рис.2

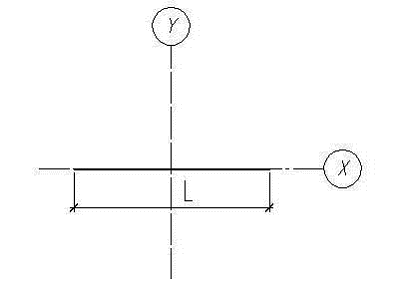
Рис.3

Таким образом, предварительно имеем 0< ξ< 0,5.
Учитывая центральную симметрию сечения (т. С, рис.1), центробежный момент инерции будем определять для верхней половины сечения (рис.4)

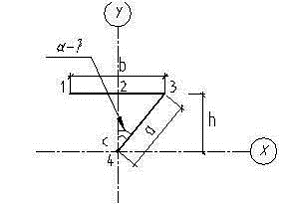
Рис.4

Предварительно решим две задачи, т.е. найдем центробежный  и осевой моменты инерции полосы толщиной δ = const (рис.5,6)

Задача №1 (рис.5):
Для , ;
Для , .
Задача №2 (рис.6):
Для ,
.

Для l:

Рис.5

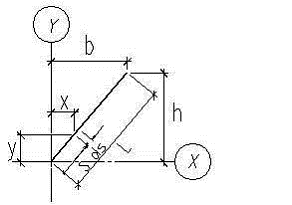
Рис.6

Тогда, из рис.4, следует, что

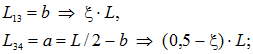
а так же
 
Из рис.4 следует, что центробежный момент инерции верхней половины сечения равен нулю, если справедливо равенство

,

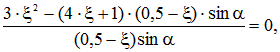Или где 
Тогда  (1)
Следовательно,  (2)
Установим окончательные пределы изменения ξ:
т.к., то имеем неравенство  
или 
или 
т.е. или .
Из системы:

окончательно имеем:

 (3)

Предельные случаи изображены:
– при α = 0 или ξ = 0 на рис. 2;
–при  или ξ = 0,348 верхняя половина сечения на рис. 7.
В заключении приведём соотношение размеров Z-образного профиля, при наиболее используемых значениях (табл.1). Введем обозначения (рис.8):

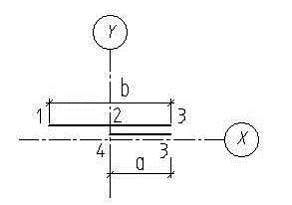
Рис. 7

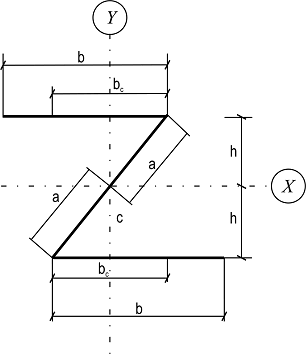
Рис. 8

Осевой момент инерции определяется по формуле:

.

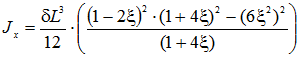Осевой момент сопротивления определяется по формуле:

причем при ξ= 0,1184 имеем 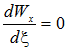 или W_x = W_max на промежутке 0<ξ<0,348.

0,1	2,3333	18,64	23,333	0,8934	1,1184
0,1184	2,0743	13,333	17,5194	0,8535	1,1215
0,15	1,7778	8,2358	11,852	0,7726	1,1118
0,2	1,5	4,3875	7,5	0,616	1,053
0,21	1,4603	3,9073	6,9538	0,5809	1,0339
0,22	1,4242	3,4847	6,4738	0,5447	1,0120
0,23	1,3913	3,1097	6,0491	0,5074	0,987
0,24	1,3611	2,7744	5,6713	0,4691	0,9588
0,25	1,3333	2,4721	5,3333	0,4297	0,927
0,26	1,3077	2,1974	5,0296	0,3894	0,8912
0,27	1,284	1,9455	4,7556	0,3482	0,8851
0,28	1,2619	1,7124	4,5068	0,3061	0,8055
0,29	1,2414	1,4941	4,2807	0,2632	0,7539
0,30	1,2222	1,2867	4,074	0,2195	0,6948
0,31	1,2043	1,0859	3,8848	0,1750	0,6262
0,3143	1,1969	1,0003	3,8081	0,1557	0,5928
0,32	1,1875	0,8859	3,7109	0,1299	0,5443
0,33	1,1717	0,6763	3,5506	0,08417	0,4419
0,34	1,1569	0,4307	3,4026	0,03782	0,2987
0,345	1,1498	0,2595	3,3328	0,01443	0,1853

1. Александров А.В., Потапов В.Д., Державин Б.П. Сопротивление материалов: Учеб. для вузов. М: Высш. шк., 1995. 560 с.
2. Власов В.З. Избранные труды. В 3 т. / Т.2 Тонкостенные упругие стержни. Принципы построения общей технической теории оболочек. М.: Изд-во АН СССР, 1963. 507с.
3. Шеин А.И. Решение многопараметрической задачи динамики стержневых систем методом сеточной аппроксимации элементов // Промышленное и гражданское строительство. 2002. № 2. С. 27-31.
4. Шеин А.И., Земцова О.Г. Снижение уровня колебаний системы «упругое основание – высотное сооружение» с помощью нелинейного динамического гасителя // Региональная архитектура и строительство. 2011. № 2. С. 83-90.

Все статьи автора «Земцова Ольга Григорьевна»