Задача описания абелевых групп без кручения конечного ранга, представимых в виде подпрямой суммы абелевых групп без кручения первого ранга впервые была поставлена Л. Я. Куликовым [1] и в настоящее время является достаточно актуальной.
В данной статье продолжено (см. [2], [3], [4]) изучение свойств подпрямых сумм бесконечных циклических абелевых групп.
Всюду в статье (если не сказано иначе) все группы – абелевы, А и В – бесконечные циклические группы: 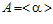 и
и 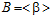 , п – целое положительное число, причем п > 1.
, п – целое положительное число, причем п > 1.
Определение. Подгруппа G прямого произведения 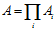 абелевых групп называется подпрямой суммой групп Аi, если для каждого i отображение
абелевых групп называется подпрямой суммой групп Аi, если для каждого i отображение 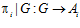 является эпиморфизмом, где
является эпиморфизмом, где 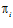 – проекция прямого произведения А на прямой сомножитель Аi [5].
– проекция прямого произведения А на прямой сомножитель Аi [5].
Как установлено [Там же], для того чтобы группа G являлась подпрямой суммой групп А и В, необходимо и достаточно, чтобы существовали группа F и такие эпиморфизмы 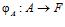 и
и 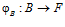 , что для любых элементов
, что для любых элементов 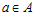 и
и 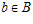 ,
, 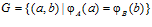
Назовем F индуцирующейч группой для подпрямой суммы G групп А и В, а эпиморфизмы 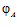 и
и 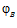 назовем определяющими для группы G.
назовем определяющими для группы G.
Обозначим: 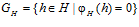 ;
; 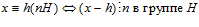 ;
; 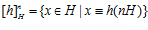 ; где Н есть либо группа А, либо группа В.
; где Н есть либо группа А, либо группа В.
Другие необходимые определения, обозначения и термины приведены в работах [1] – [10].
Определение. Если для некоторого данного числа п, большего 1, группа G является подпрямой суммой данных групп А и В, порожденной конечной циклической группой Zп – аддитивной группой кольца вычетов по модулю п, – то группу G будем называть элементарной специальной п-группой (esп-группой).
ТЕОРЕМА I. Между множеством esп-групп и множеством автоморфизмов группы Zп – аддитивной группы кольца вычетов по модулю n – существует взаимно однозначное соответствие. [4]
ПРЕДЛОЖЕНИЕ 1. Пусть G – esn-группа, и пусть 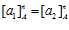 и
и 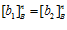 , где
, где 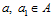 и
и 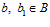 . Тогда
. Тогда 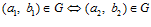 .
.
Доказательство. По определению подпрямой суммы имеем: 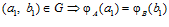 . Из условия получаем:
. Из условия получаем:
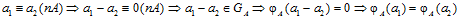 .
.
Аналогично выводим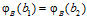 . Откуда, следует, что
. Откуда, следует, что 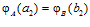 , то есть
, то есть 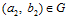 .
.
Обратное утверждение доказывается обращением приведенных рассуждений.
СЛЕДСТВИЕ. Пусть G – esп-группа, и пусть 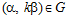 для некоторого целого числа
для некоторого целого числа 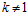 . Тогда
. Тогда 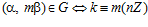 для любого целого числа т.
для любого целого числа т.
Доказательство непосредственно следует из предложения 1.
ПРЕДЛОЖЕНИЕ 2. Пусть G – esn-группа, и пусть 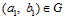 и
и 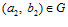 , где
, где 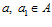 и
и 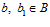 . Тогда
. Тогда 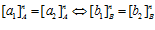 .
.
Д о к а з а т е л ь с т в о. Пусть 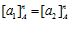 , то есть
, то есть 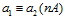 , следовательно, по определению esп-группы,
, следовательно, по определению esп-группы, 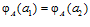 . По условию имеем:
. По условию имеем: 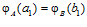 и
и 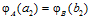 . Откуда получаем:
. Откуда получаем: 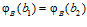 и, следовательно,
и, следовательно, 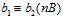 , то есть
, то есть 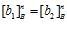 .
.
Обратное утверждение доказывается обращением изложенных выводов.
Введем следующие обозначения:
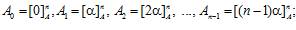
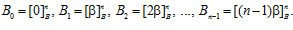
ТЕОРЕМА II.
1. Группа G является esn-группой тогда и только тогда, когда для некоторого автоморфизма g группы Zn:
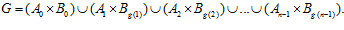
Такой автоморфизм g группы Zn мы будем далее называть склеиванием esn-группы G.
2. Для любого автоморфизма g группы Zn, группа
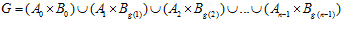
является esn-группой.
Доказательство непосредственно следует из теоремы I.
ПРЕДЛОЖЕНИЕ 3. Пусть G и G’– esn-группы со склеиваниями g и g’, соответственно. Тогда существует автоморфизм f группы Zп такой, что g’ = fg.
Наоборот, если g – склеивание esn-группы G, то для любого автоморфизма f группы Zп автоморфизм g’ = fg будет, очевидно, склеиванием для некоторой esn-группы G‘.
Доказательство. Пусть g(1) = m, g’(1) = k. И пусть f – автоморфизм группы Zn такой, что f(k) = m. Тогда, очевидно, имеет место равенство g’ = fg.
Обратно. Пусть g – склеивание esn-группы G, f – автоморфизм группы Zn. Если 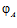 и
и 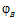 – определяющие эпиморфизмы группы G, то в качестве определяющих эпиморфизмов искомой группы G’ выберем отображения
– определяющие эпиморфизмы группы G, то в качестве определяющих эпиморфизмов искомой группы G’ выберем отображения 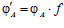 и
и 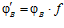 .
.
ПРЕДЛОЖЕНИЕ 4. Пусть G и G’ – esn-группы. Тогда 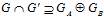 . Причем равенгство выполняется тогда и только тогда, когда число п является простым.
. Причем равенгство выполняется тогда и только тогда, когда число п является простым.
Доказательство. По определению попрямой суммы групп и esn-группы, прямая сумма 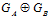 является подгруппой каждой esn-группы G. С другой стороны, по теореме I, если
является подгруппой каждой esn-группы G. С другой стороны, по теореме I, если 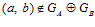 , где
, где 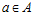 ,
, 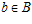 , и п – простое число, то существует единственная esn-группа G, такая что
, и п – простое число, то существует единственная esn-группа G, такая что 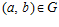 , из чего и следует требуемое условие.
, из чего и следует требуемое условие.
СЛЕДСТВИЕ. Для любого натурального числа п > 1, существуют единственная esn-группа G, такая что бесконечная циклическая группа 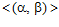 есть собственная подгруппа группы G, и единственная esn-группа G‘, такая что бесконечная циклическая группа
есть собственная подгруппа группы G, и единственная esn-группа G‘, такая что бесконечная циклическая группа 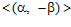 есть собственная подгруппа группы G‘.
есть собственная подгруппа группы G‘.
Доказательство непосредственно следует из предложения 4.
ПРЕДЛОЖЕНИЕ 5. Пусть G – esn-группа, причем для некоторого целого числа т,
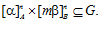
Тогда числа п и т являются взаимно простыми.
Наоборот, для любого числа т взаимно простого с числом n, существует единственная esn-группа G такая, что 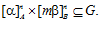
Доказательство. Предположим, что 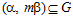 , и наибольший общий делитель чисел п и m равен k > 1. Тогда, по определению НОД, существуют целые числа r и s такие, что
, и наибольший общий делитель чисел п и m равен k > 1. Тогда, по определению НОД, существуют целые числа r и s такие, что
m = kr, n = ks, (1)
причем, очевидно, что s < п, и 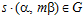 , но
, но 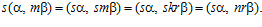 Следовательно,
Следовательно, 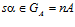 , то есть число n делит число s, что противоречит равенству (1). Значит, предположение о том, что наибольший общий делитель чисел п и m больше 1 неверно, то есть числа п и m взаимно просты. Обратное утверждение непосредственно следует из теоремы I. Предложение доказано.
, то есть число n делит число s, что противоречит равенству (1). Значит, предположение о том, что наибольший общий делитель чисел п и m больше 1 неверно, то есть числа п и m взаимно просты. Обратное утверждение непосредственно следует из теоремы I. Предложение доказано.
ПРЕДЛОЖЕНИЕ 6. Пусть G – esn-группа, и пусть t – целое число, взаимно простое с числом п. Если 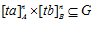 , где
, где 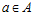 ,
,
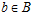 , то
, то 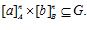
Доказательство. Из определения подпрямой суммы групп А и В следует, что для любого элемента 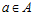 найдется такой элемент
найдется такой элемент 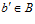 , что
, что 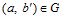 . Но тогда, легко видеть,
. Но тогда, легко видеть, 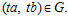 Следовательно,
Следовательно, 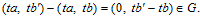 Но тогда
Но тогда 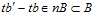 . А так как, числа t и п взаимно просты, то отсюда следует, что
. А так как, числа t и п взаимно просты, то отсюда следует, что 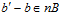 , то есть
, то есть 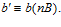 Тогда, по предложению 2, получаем, что также
Тогда, по предложению 2, получаем, что также 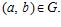 Что и требовалось доказать.
Что и требовалось доказать.
Далее, через G(т) обозначим esn-группу, для которой склеивание g задается условием: g(1) = т.
ТЕОРЕМА III. Пусть каждое из чисел т, r и s взаимно просто с числом п. Тогда имеет место следующее утверждение:
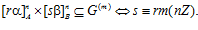
Доказательство. Пусть 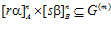 , следовательно,
, следовательно, 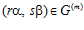 . Тогда, так как, по определению склеивания,
. Тогда, так как, по определению склеивания, 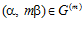 , то, очевидно, также
, то, очевидно, также 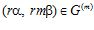 . Следовательно, по предложению 1, в группе В:
. Следовательно, по предложению 1, в группе В: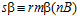 , или, что равносильно, в кольце Z:
, или, что равносильно, в кольце Z: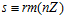 .
.
Поскольку, все данные выше рассуждения легко обратимы, то отсюда получаем обратное утверждение.
СЛЕДСТВИЕ. Пусть каждое из чисел т и r взаимно просто с п. Тогда имеет место следующее утверждение
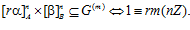
Доказательство непосредственно следует из теоремы.
ТЕОРЕМА IV. Пусть G – esn-группа, и пусть для некоторых элементов 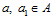 , и
, и 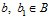 , каждый из классов
, каждый из классов 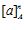 ,
, 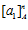 и каждый из классов
и каждый из классов 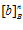 ,
, 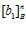 взаимно прост с классами
взаимно прост с классами 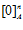 и
и 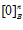 , соответственно. Если
, соответственно. Если 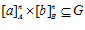 и
и 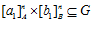 , то существует целое число r, взаимно простое с п такое, что
, то существует целое число r, взаимно простое с п такое, что 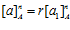 ,
, 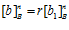 . Причем число r единственно с точностью до сравнения по модулю n.
. Причем число r единственно с точностью до сравнения по модулю n.
Доказательство. Пусть 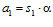 ,
, 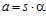 , где s1, s – целые числа, каждое из которых взаимно просто с числом п. Как известно, для некоторого целого числа r, взаимно простого с числом п, имеет место сравнение
, где s1, s – целые числа, каждое из которых взаимно просто с числом п. Как известно, для некоторого целого числа r, взаимно простого с числом п, имеет место сравнение 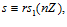 из которого, очевидно, вытекает сравнение
из которого, очевидно, вытекает сравнение 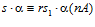 , или равносильное сравнение
, или равносильное сравнение 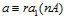 . Поскольку,
. Поскольку, 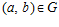 , то и, очевидно,
, то и, очевидно, 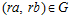 . Следовательно, по предложению 2, в группе В имеет место сравнение
. Следовательно, по предложению 2, в группе В имеет место сравнение 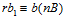 .
.
Откуда получаем равенства: 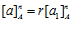 ,
, 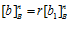 . Теорема доказана.
. Теорема доказана.
Библиографический список
- Куликов Л. Я. О подпрямых суммах абелевых групп без кручения первого ранга // ХII Всесоюзный алгебраический коллоквиум. Свердловск, 1973.
- Трухманов В. Б. О некоторых специальных и р-специальных группах // Исследования в области естественных наук. 2014. № 6 (30). С. 5.
- Трухманов В. Б. О подгруппах прямой суммы бесконечных циклических абелевых групп // Исследования в области естественных наук. 2014. № 7 (31). С. 45-50.
- Трухманов В.Б. О подпрямых суммах бесконечных циклических абелевых групп // Альманах современной науки и образования. 2014. № 9 (87). С. 131-134.
- Фукс Л. Бесконечные абелевы группы. М.: Мир, 1974. Т. 1.
- Широков Л.В. Внешняя характеристика пространств Дугунджи и ‑метризуемых бикомпактов. // Докл. АН СССР. 1982. т. 263. № 5. С. 1073-1077.
- Широков Л.В. О -бикомпактах и n-мягких отображениях. // Сиб. матем. журн. 1992. т. 33. № 2. С. 151-156.
- Широков Л.В. Современные вопросы радиоэлектроники с позиций теории аналитических функций /Л. В. Широков, Н. П. Ямпурин, В. А. Потехин, В. Д. Садков. -Арзамас: АГПИ, 2008. -176 с.
- Shirokov L.V. On some forms of embeddings of topological spaces. // Russian Mathematical Surveys 42, (2), 297-298.
- Trukhmanov V. B. On subdirect sums of abelian torsion-free groups of rank 1. // Journal of Mathematical Sciences. 2008. Vol.154. №3. – P. 422-429.
