Введение.

Пожалуй, самый известный из всех парадоксов теории относительности это «Парадокс близнецов» или «Парадокс часов». Разъяснение этого парадокса еще в 1918 г. дал сам А. Эйнштейн в статье «Диалог по поводу возражений против теории относительности» [1 с.616-625]. В этой работе описан следующий мысленный эксперимент. Пусть А и В – две удаленные друг от друга точки неподвижной системы К. Пусть U₁ и U₂ – двое совершенно одинаковых часов, расположенных в точке А и показывающих одинаковое время. Сообщим часам U₂ некоторую постоянную скорость к точке В. Пусть в точке В скорость часов U₂ меняется на противоположную и по возвращении в точку А они останавливаются. Так как наблюдаемое из К изменение показаний часов U₂, произошедшее при их развороте, имеет некоторую конечную величину, и так как часы U₂ при движении вдоль отрезка АВ идут медленнее часов U₁, то при достаточно большой длине отрезка АВ часы U₂ по возвращении в точку А должны отставать от часов U₁ на некоторое время ∆t₁. Если процесс перемещения часов U₂ в точку В и обратно рассмотреть относительно системы К′, связанной с часами U₂, в которой они неподвижны, то, учитывая неравноправность К и К′ (вследствие неинерциальности К′), для расчета показаний часов U₁ необходимо привлечение общей теории относительности. В этом случае, как утверждается в вышеупомянутой статье, суммарное отставание часов U₁ от U₂ на Δt₁ на участках постоянной скорости часов U₁ относительно К′ компенсируется их уходом вперед на Δt₂ во время разворота в гравитационном поле, возникающем в неинерциальной системе К′, причем:

Δt₂ = 2·Δt₁

Таким образом, суммарно, как и в случае рассмотрения процесса относительно системы К, часы U₂ будут отставать от U₁ на Δt₁, т.е. никакого противоречия нет.

В своей статье Эйнштейн не приводит расчетов, но такие расчеты можно найти, например, в книге М. Борна «Эйнштейновская теория относительности» [2 с.343-346]. В этих расчетах для сравнения длительности путешествия по часам U₁ и U₂ используются приближенные формулы (как в системе отсчета K, так и в системе отсчета К′), которые получены для случая движения часов U₂ вдоль прямой линии, при этом их разворот осуществляется путем торможения и последующего разгона в обратном направлении. Применимость этих приближенных формул обоснована двумя основными допущениями. Первое допущение заключается в том, что расстояние L между часами при развороте (отрезок AB) предполагается сколь угодно большим по сравнению с участком разворота. Второе допущение заключается в том, что при рассмотрении разворота часов U₁ в гравитационном поле g системы отсчета К′ расстояние L между часами должно быть ограничено соотношением [2 с.343; 3 с.305-306; 5 с.205]:

g∙L/c² << 1,

то есть не может быть сколь угодно большим. Как видим, использованные допущения взаимно исключают друг друга. Первое предполагает сколь угодно большую длину отрезка AB, а второе это запрещает. Данное противоречие можно устранить отказавшись от первого допущения, т.е. от сколь угодно большой длины отрезка AB по сравнению с участком разворота. Покажем, что это можно сделать, причем совершенно не усложняя расчетов. Рассмотрим похожий мысленный эксперимент, немного изменив траекторию движения часов U₂. Это изменение позволит нам для сравнения показаний часов U₁ и U₂ использовать не приближенные, а точные формулы теории относительности.

 

Разворот по дуге окружности.

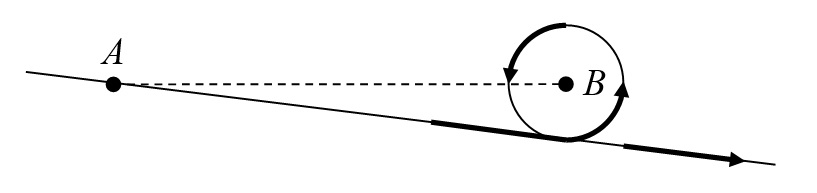
Пусть при развороте часы U₂ не тормозят, а продолжают лететь с той же скоростью V, но по дуге радиуса r вокруг точки B (рис. 1), представляющей собой часть окружности. Причем прямые части траектории часов U₂ являются касательными к этой окружности, что исключает скачкообразное изменение направления скорости часов U₂ в точках начала и конца разворота, и обеспечивает, так сказать, «бесшовный» переход от равномерного и прямолинейного движения к движению по окружности, и обратно. Угловая скорость вращения часов U₂ вокруг точки B на участке разворота будет равна:

ω = V/r

Чтобы без потери точности расчетов исключить необходимость рассмотрения неинерциальных участков разгона и торможения часов U₂ в точке A, немного изменим для часов U₁ и U₂ порядок их синхронизации на старте и сверки показаний на финише. Пусть часы U₂ не разгоняются в точке A, а пролетают мимо нее со скоростью V в направлении к точке B и синхронизируются с часами U₁ в момент их совмещения. На обратном пути часы U₂ не останавливаются в точке A, а пролетают мимо с той же скоростью, сверяя свои показания с часами U₁ в момент их совмещения.

Рис. 1. Разворот часов U₂ в точке B по окружности.

 

Рассмотрим сначала ситуацию с точки зрения системы отсчета К′, связанной с часами U₂. Суммарное время ΔT′_U2, прошедшее по часам U₂ между событиями первой и второй встречи с часами U₁, равно:

ΔT′_U2 = ∆τ′_U2 + ∆t′_U2                                                                        (1)

где:

∆t′_U2 – время разворота по часам U₂;

∆τ′_U2 – суммарное время, прошедшее по часам U₂ на участках равномерного и прямолинейного движения.

Суммарное время ΔT′_A, прошедшее по часам U₁ между событиями первой и второй встречи с часами U₂, равно:

ΔT′_A = ∆τ′_A + ∆t′_A                                                                                     (2)

где:

Δt′_A – время разворота по часам U₁;

∆τ′_A – суммарное время, прошедшее по часам U₁ на участках равномерного и прямолинейного движения.

Учитывая, что согласно специальной теории относительности на участках равномерного и прямолинейного движения с точки зрения часов U₂ движущиеся часы U₁ идут медленнее в γ раз [1 с.74, 156; 2 с.243, 344], имеем:

∆τ′_U2 = γ∙∆τ′_A                                                                                  (3)

где:

γ = (1 – V ²/c²) ^–1/2 – Лоренц-фактор;

с – скорость света.

На участке разворота система К′ является вращающейся системой отсчета с центром в точке B, поэтому в ней существует гравитационное поле, в котором часы U₂ неподвижны, а часы U₁, вращаются с угловой скоростью ω вокруг неподвижной точки B, где находятся точно такие же часы U_B. Теория относительности ограничивает использование системы отсчета К′ на участке разворота следующим условием [4 с.329; 5 с.182]:

R < с/ω = с∙r/V,

которое для любых R и r всегда может быть соблюдено соответствующим выбором скорости V, не равной нулю.

Во вращающейся системе отсчета темп хода часов U₁ и U_B одинаков [5 с.211-212], т.к. в инерциальной системе отсчета K они неподвижны и являются так называемыми «координатными» часами [5 с.184]. В самом деле, предположим, что это не так. Тогда, если в системе К′ до начала вращения показания часов U₁ и U_B отличались на некоторую величину, то совершив достаточно много оборотов по окружности вокруг точки B, а потом вернувшись на прежнюю прямолинейную траекторию (рис. 2), их показания отличались бы уже на другую величину (в системе K при этом вращались бы, а потом вернулись на прежнюю траекторию часы U₂).

Рис. 2. Переход от прямолинейного движения к движению по окружности и обратно на ту же прямолинейную траекторию.

 

Получается, что мы вернулись в ту же инерциальную систему отсчета, в которой находились до начала вращения (она движется с той же скоростью и в том же направлении), но теперь показания часов U₁ и U_B отличаются на другую величину, зависящую от количества оборотов, сделанных часами U₂ по окружности. Это означает, что показания часов U₁ и U_B зависят не только от скорости системы отсчета К′ (которая до и после движения по окружности является инерциальной), но и от предыстории движения часов U₂, а это очевидный абсурд.

Так как часы U_B и U₁ на участке разворота идут с одинаковым темпом, а часы U₂ в γ раз медленнее [5 с.183, 200; 6 с.309], имеем:

Δt′_A = Δt′_B = γ∙∆t′_U2                                                                         (4)

где:

γ = (1 – ω²∙r²/c²) ^–1/2       – Лоренц-фактор;

Δt′_B – время разворота по часам U_B.

Подставляя (3) и (4) в (1), получим:

ΔT′_U2 = γ∙∆τ′_A + Δt′_A/γ                                                                     (5)

Рассмотрим теперь ситуацию с точки зрения системы отсчета К, связанной с часами U₁. Пусть ΔT_A это собственное время, прошедшее по часам U₁ между событиями первой и второй встречи с часами U₂, тогда интервал ΔT′_A, который является по сути прогнозом величины интервала ΔT_A, полученным в системе отсчета К′ на основе теории относительности, должен быть ему равен (в противном случае теория относительности дает неверный прогноз). Действительно, если часы U₁ и U₂ при синхронизации в момент первой встречи (на старте) установлены на ноль, то в момент второй встречи (на финише) наблюдатель, находящийся рядом с часами U₁, увидит на них время ΔT_A, а наблюдатель, находящийся рядом с часами U₂, должен увидеть на часах U₁ время ΔT′_A. Очевидно, что наблюдатели, находясь в одной и той же точке пространства и в один и тот же момент времени (на финише), не могут видеть разные показания на одних и тех же часах U₁, поэтому, с учетом (2), имеем:

ΔT_A = ΔT′_A = ∆τ′_A + ∆t′_A                                                                         (6)

В системе отсчета К часы U₂ все время двигаются со скоростью V. Учитывая, что согласно специальной теории относительности с точки зрения часов U₁ часы U₂ идут медленнее в γ раз [1 с.74, 156; 2 с.243, 344], получаем, что время ΔT_U2, затраченное часами U₂ на путешествие, должно быть равно:

ΔT_U2 = ΔT_A/γ                                                                                  (7)

Подставляя в (7) выражение для ΔT_A из (6), найдем:

ΔT_U2 = ∆τ′_A/γ + ∆t′_A/γ                                                                      (8)

Интервал ΔT_U2 является по сути прогнозом собственного времени ΔT′_U2 (времени, прошедшего по часам U₂ между событиями первой и второй встречи с часами U₁), рассчитанным в системе отсчета К на основе теории относительности, поэтому должен быть ему равен (в противном случае теория относительности дает неверный прогноз).  Действительно, если часы U₁ и U₂ при синхронизации в момент первой встречи (на старте) установлены на ноль, то в момент второй встречи (на финише) наблюдатель, находящийся рядом с часами U₂, увидит на них время ΔT′_U2, а наблюдатель, находящийся рядом с часами U₁, должен увидеть на часах U₂ время ΔT_U2. Очевидно, что наблюдатели, находясь в одной и той же точке пространства и в один и тот же момент времени (на финише), не могут видеть разные показания на одних и тех же часах U₂. Это дает нам право приравнять выражения (5) и (8), в результате получим:

γ∙∆τ′_A + Δt′_A/γ = ∆τ′_A/γ + ∆t′_A/γ

и после преобразования:

γ = 1/γ

Очевидно, что для любой скорости V ≠ 0 это равенство может быть истинным только в случае с → ∞, при этом преобразования Лоренца переходят в преобразования Галилея. Таким образом, действуя строго в рамках теории относительности мы пришли к противоречию с ее основным постулатом.

Напомним, что в представленных выше расчетах мы не использовали никаких приближений, следовательно, и все полученные соотношения должны быть абсолютно точны. Таким образом, рассмотренный мысленный эксперимент, не смотря на то, что он вполне физически реализуем, тем не менее не может быть непротиворечиво описан в рамках теории относительности.

Библиографический список

1. Эйнштейн А. Собрание научных трудов. В 4 т. Т.I. Работы по теории относительности 1905-1920; под редакцией И.Е. Тамма, Я.А. Смородинского, Б.Г. Кузнецова. – М.: НАУКА, 1965. – 700 с.
2. Борн М. Эйнштейновская теория относительности, перевод с английского Н.В. Мицкевича. – 2-е изд., испр. – М.: МИР, 1972 (EINSTEIN’S THEORY OF RELATIVITY by Max Born. Revised edition prepared with the collaboration of Gunter Leibfried and Walter Biem. Dover Publications Inc. New York 1962)
3. Фок В.А. Теория пространства, времени и тяготения. – 2-е изд., дополненное. – М.: Государственное издательство физико-математической литературы, 1961
4. Ландау Л.Д., Лившиц Е.М. Теоретическая физика: Учеб. пособие. В 10 т. Т.II. Теория поля. – 7-е изд., испр. – М.: НАУКА, 1988. – 512 с. – ISBN 5-02-014420-7
5. Мёллер К. Теория относительности. – 2-е изд. – Пер. с англ. Под ред. проф. Д. Иваненко. – М.: Атомиздат, 1975 (The Theory of Relativity by C. Möller, second edition, Clarendon press, Oxford, 1972)
6. Тоннела Мари-Антуанетт, Основы электромагнетизма и теории относительности, перевод с французского Г.А. Зайцева. – М: Издательство иностранной литературы, 1962 (Marie-Antoinette TONNELAT, Professeur a la Faculte des Sciences de Paris, LES PRINCIPES DE LA THEORIE ELECTROMAGNETIQUE ET DE LA RELATIVITE; MASSON ET C^IE, EDITEURS; PARIS, 1959)

---

Количество просмотров публикации: Please wait

Все статьи автора «Бузмаков Игорь Витальевич»