1. Introduction
Radioactive radiation is one of the major natural and man-made factors affecting human life and health. Due to recent changes in the conceptual approach, the problem of radiation safety comes not only to ensure the control of a limited number of potentially dangerous objects (plants and laboratories of nuclear fuel cycle, research and defense facilities of the appropriate profile, etc.), but becomes more global [1, p. 11]. Up to 70% of radiation is contributed by natural gamma-emitting radionuclides contained in the building materials and as a result, there is uncontrolled proliferation of these radionuclides in building construction, including walls and ceilings of residences. For example, radiation sources are: residential, public and industrial buildings and asphalt and other road surfaces. People spend 80% of their time indoors, which means that a significant portion of radiation exposure they get from building materials.
Concentration of radionuclides in building materials depends on the geographical location of their raw material, as well as the processing technology. Yes, the background radiation can be high in areas of granite deposits, and the concentration of radionuclides in the production of cement is 36% higher than the raw stuff. Using of panels made of slag of blast furnaces slag and cinder blocks and panels of phosphogypsum leads to an increase in dose rate in residential areas by 5-10 times in comparison with that in stretch of open country.
With regard to natural radiation, the deeper lying material used for the production of building materials, the greater the likelihood of its higher level of radiation. It is known that about 3% of building materials possess the concentration of radionuclides that exceeds the norm. When using construction materials with high concentrations of radionuclides, the dose of radiation increses.
Most countries, especially in Europe, have introduced relevant legislation in the field of building materials and construction, whereby the radiation monitoring in this field should be mandatory. To avoid high radiation levels in premises, the authority of sanitary-epidemiological surveillance conducted three phased radiation monitoring. The first stage is the radiation control of raw materials from which construction materials (sand, gravel, stone, clay, gypsum, etc.) are produced. The second stage is the control of materials at their production; for example, if a plant produces bricks or concrete, these materials must undergo such test. The third stage is a mandatory inspection of already constructed objects, namely, new residences and buildings after reconstruction or renovation.
Control of the presence of radioactive elements in samples of building materials can be made only by special dosimetric and spectrometric instrumentation [2, p. 107]. However, the detection of low-level radioactive sources is a difficult task, which is caused, on the one hand, by a low intensity of their radiation, and on the other hand, by the presence of an existing background radiation. The intensity of radiation of building materials is hidden in a natural background and the Compton scattering, which greatly reduces and makes it unlikely their timely detection. Also, the low intensity radiation of building materials we get owing to a comparative distant location of the detector. It is particularly important and difficult to identify building materials with a high content of radionuclides during their transportation.
The solution of this problem requires new approaches to the problem of registration of radiation. It is necessary to use new modern, reliable and economical methods for detection and identification of radiation. Functional capabilities of specialized technical means, which are now used for radiation monitoring of building materials, do not allow one to realize the problem of detection and control unauthorized movement of low-level radioactive materials that are characterized by occasional, short and slight excess information signals above the background.
The reliability and accuracy of measurements in radiation monitoring of building materials are determined by both technical and functional capabilities of the equipment, as well as the algorithmic basis with the appropriate software. The most significant contribution to the realization of maximum sensitivity of the technial means brings the efficiency of detectors that record the radiation and the power of statistical data processing algorithms. In practice among the methods of analysis of radiation most often used spectrometric methods for the identification of low-level radioactive sources.
The spectrometric method is based on the measurement of energy spectrum of radiation sources. As a result of measurement one obtains a not true gamma spectrum, but the so-called discrete spectrum of radiation, which is a histogram of the distribution of pulses by energy channels of the analyzer in accordance with the channels’ amplitudes. Using this spectrometer one can determine both the number of pulses and the energy of each pulse.
In spectrometric devices primary information comes in the form of a random sequence of pulses from the detectors that record radiation. In addition to registration of useful events, such information contains a number of obstacle signals caused by background radiation, electromagnetic fields, etc., leading to uncertainty. Thus the main task, which must implement technical facilities, is to detect slight increase in the radiation field in places of observation and control, as well as the identification of the appropriate sources.
Mathematically, the problem of detection and identification of radiation can be described as follows. Suppose, in a time t [0, T] of the continuous observation of a source of radiation we record n radioactive particles. The measurement forms a selection 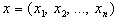 of the general population and the allocation of each
of the general population and the allocation of each 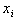 is described by the Poisson distribution. The sample x is between fixed values
is described by the Poisson distribution. The sample x is between fixed values 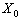 and
and 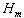 . Chance of getting the measured value of x in the interval from
. Chance of getting the measured value of x in the interval from 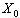 to
to 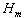 is described by the distribution function [3, p. 135].
is described by the distribution function [3, p. 135].
Let us denote the frequency of event of “getting radiation” in the bit interval 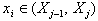 as
as 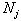 . A statistical series grouped in such a way is the so-called histogram – a statistical analogous of the distribution curve. If each bit interval puts in correspondence with the energy of the registered particle, we obtain the spectral distribution of energy radiation.
. A statistical series grouped in such a way is the so-called histogram – a statistical analogous of the distribution curve. If each bit interval puts in correspondence with the energy of the registered particle, we obtain the spectral distribution of energy radiation.
In control and monitoring of the source of radiation by the method of spectrometric analysis it is necessary to distinguish in the background spectrum a signal or spectrum that belongs to the radiation source. That is, one should identify the sudden appearance of radiation of a radioactive source by analyzing spectra (the background and the source of radiation), which are obtained by observation. Or, on the basis of statistical data one has to reveal a jumpy change in the spectrum at low external influences. If it is needed to detect a source of radiation of low activity (whose activity is at the level of the natural background), the problem becomes so complicated that standard methods is rather unable to do this. To resolve the problem, we propose below a new approach based on the method of probabilistic analysis of histogram spectra of radiation.
2. The control method of sudden appearance of a radiation source based on the Bayesian approach
To control the sudden appearance of radioactive sources with activity that is at, or slightly higher than the background we will use the Bayesian approach to the estimation of unknown parameters.
Having doing this, we need to find the distribution of a parameter 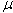 (considered as a random variable) with an available observation x. By the Bayes theorem, a posteriori distribution is calculated from the a priori probability distribution with density
(considered as a random variable) with an available observation x. By the Bayes theorem, a posteriori distribution is calculated from the a priori probability distribution with density 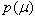 and the likelihood function
and the likelihood function 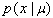 by the formula [4]:
by the formula [4]:
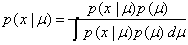 , (1)
, (1)
If the posteriori distribution 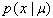 belongs to the same family of probability distributions as the a priori distribution
belongs to the same family of probability distributions as the a priori distribution  (i.e., has the same form, but with different parameters), this family of distributions is called a paired family of likelihood functions
(i.e., has the same form, but with different parameters), this family of distributions is called a paired family of likelihood functions  . For conjugate families of distributions the culculation of posteriori probabilities in the Bayesian statistics is greatly simplified.
. For conjugate families of distributions the culculation of posteriori probabilities in the Bayesian statistics is greatly simplified.
Let the random selection x is described by a distribution with unknown mean 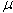 and known variance
and known variance 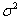 (according to the central limit theorem, when
(according to the central limit theorem, when 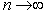 the Poisson distribution passes into the normal law). A priori distribution of the parameter
the Poisson distribution passes into the normal law). A priori distribution of the parameter 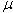 describes the normal law with expectation
describes the normal law with expectation 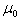 and variance
and variance 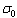 . Then for conjugate families of distributions the posteriori distribution of the parameter
. Then for conjugate families of distributions the posteriori distribution of the parameter 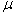 is normal with an average
is normal with an average
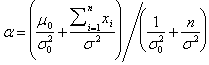 , (2)
, (2)
and the dispersion
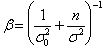 . (3)
. (3)
At the radiation control and monitoring of sources of radiation by the method of spectrometric analysis the information from detectors arrives as a series of spectra 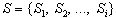
 . Each spectrum
. Each spectrum  comes into the system for processing in a (given) discrete time interval
comes into the system for processing in a (given) discrete time interval 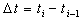 (the accumulation of pulses). The time interval
(the accumulation of pulses). The time interval 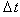 of accumulation of pulses in the spectrum will determine the time within which the presence of a source of radiation has to be detected. To determine parameters of the a priori distribution of a signal
of accumulation of pulses in the spectrum will determine the time within which the presence of a source of radiation has to be detected. To determine parameters of the a priori distribution of a signal  , we will use the information about prehistory. Let us consider the set of measurements for the previous period
, we will use the information about prehistory. Let us consider the set of measurements for the previous period  . The size of selections (spectra
. The size of selections (spectra  ), which are considered, is independent of the accumulation time and the intensity of radiation and depends only on the detection device used. For modern devices the size of selection is constant and equal to 1024, 2048 or 4096 values.
), which are considered, is independent of the accumulation time and the intensity of radiation and depends only on the detection device used. For modern devices the size of selection is constant and equal to 1024, 2048 or 4096 values.
To identify and determine the source of radiation in the field of the detector, the intensity of which is slightly higher than the background level, it is necessary to formulate a statistical criterion [5].
If a Bayesian average  of pulses
of pulses 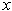 of radiation in the
of radiation in the 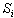 spectrum deviates from the mean value
spectrum deviates from the mean value 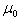 in the
in the 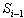 spectrum by three standard deviation values for the Bayesian average, then a source of radiation is present:
spectrum by three standard deviation values for the Bayesian average, then a source of radiation is present:
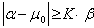 ,
, 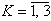 . (4)
. (4)
Such criterion has allowed us to develop a method and algorithm for detecting the sudden appearance of radioactive sources. The algorithm includes the following steps:
Step 1. We expect a priori parameters of the distribution (a priori mean value 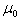 and the mean square deviation
and the mean square deviation 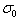 ) on the basis of spectra
) on the basis of spectra 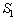 ,
, 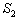 , …,
, …, 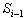 by the formulas
by the formulas
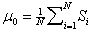 , (5)
, (5)
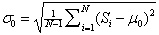 , (6)
, (6)
where  is the integral value of the spectrum,
is the integral value of the spectrum,  is the dimension of the preview window
is the dimension of the preview window  ,
, 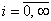 .
.
Step 2. On the basis of ,
,  , …,
, …,  ,
, 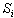 spectra we calculate parameters
spectra we calculate parameters 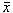 and
and 
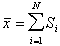 (7)
(7)
where 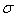 is calculated by expression (6).
is calculated by expression (6).
Step 3. Determine values of 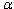 and
and  parameters by expressions (2) and (3) of the posteriori distribution.
parameters by expressions (2) and (3) of the posteriori distribution.
Step 4. Use the statistical criterion of identification of the emergence of a source of radiation. If 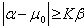 ,
, 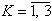 , then we can determine the presence of a source of radiation. Otherwise, no source.
, then we can determine the presence of a source of radiation. Otherwise, no source.
Step 5. Increment the index 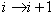 . Wait for the arrival of a new spectrum,
. Wait for the arrival of a new spectrum, 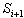 , and go to Step 1 for the study of data of the new spectrum.
, and go to Step 1 for the study of data of the new spectrum.
3. A study of the method of probability
Studying the proposed method, a series of test experiments was conducted. Measurements conducted spectrometer with scintillation detector of the type BDEG, 4-31 (block for detecting gamma-radiation). Block diagram of the spectrometer is shown in Fig. 1.
Results obtained at measurements in times  and
and  of histograms of energy radiation with the same area (the values were obtained during the 1-minute measurement) were compared with the criterion (4) for
of histograms of energy radiation with the same area (the values were obtained during the 1-minute measurement) were compared with the criterion (4) for 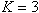 in the above algorithm. The value of criterion
in the above algorithm. The value of criterion 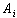 for each moment of time
for each moment of time 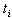 of measurements was calculated. Trends of initial spectra are depicted in Fig. 2, 3, and 4 (left). The corresponding trends of values of the criterion are exhibited in Fig. 2, 3, and 4 (right). In the experiment 1 (Fig. 2) we calculated the criterion for the background radiation.
of measurements was calculated. Trends of initial spectra are depicted in Fig. 2, 3, and 4 (left). The corresponding trends of values of the criterion are exhibited in Fig. 2, 3, and 4 (right). In the experiment 1 (Fig. 2) we calculated the criterion for the background radiation.
In the experiment 2 (Fig. 3) we introduced in the field of view of the detector a testing point source of gamma radiation (137Cs, 661.7 keV) for 10 seconds. The criterion was calculated for this case as well. The adding radiation source was performed at 31, 91 and 121 minutes; the time of accumulation of the spectrum was 1 min.
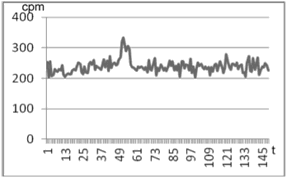
In the experiment 3 (Fig. 4) we calculated the criterion at a short (less than 5 s) and longer (over 10 s) introduction of the gamma source. The adding radiation source was run at 11 and 51 minutes. To calculate the criterion, we used the viewport range  (number of histograms), which corresponded to the 5 minute time.
(number of histograms), which corresponded to the 5 minute time.
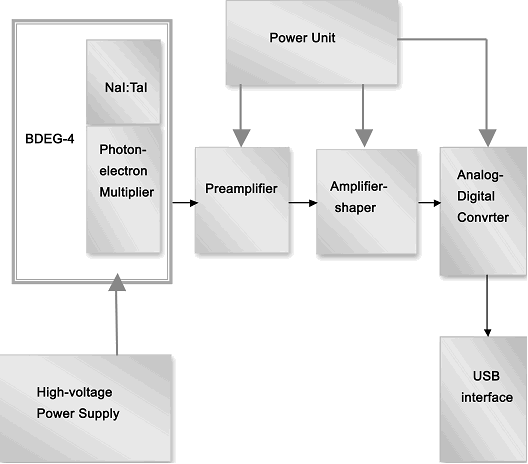
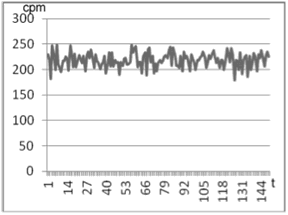
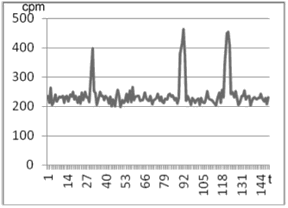
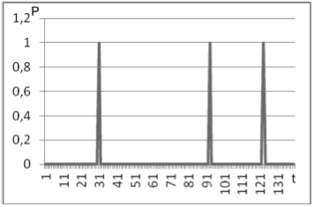
Figure 3. Experiment 2; left: Data of background radiation; right: Trend values of the criterion (4) for background radiation.

We have proposed the probabilistic method and algorithm for detecting sudden appearance of radioactive sources in the field of view of the detector, which is based on the use of Bayesian approach for the estimation of parameters and the known statistical criterion.
The method allows us to detect abrupt changes in the integral value of the background radiation intensity (of the total size of selection, or the area of interest) when the value exceeds the allowable limit.
The proposed probabilistic method for detecting a low intense radioactive source has the following advantages:· A small number of mathematical operations in the implementation of the method, which is based on the Bayes theorem for statistics, allows us to evaluate the degree of inconsistency of histograms in real time;
· The experimental data show that the proposed criterion is the sensitive quantitative indicator of any source of radiation. The sensitivity criterion is given by the coefficient
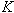 ;
;· The method does not require additional technical equipment;
· The method is characterized by high efficiency, allowing one to record the appearance of any source of radiation, even when it moves;
· The method of detecting a low intense source of radiation is capable to improve the existing methods of radiation monitoring of construction materials in both the steady state and in the state of motion.
References
- Marhulys, U. Ya., Bregadze, U. I., 2000. Radiation safety. The principles and means of ensuring. Editorial URSS, Moscow (in Russian).
- Zabulonov, Y. L., Burtnyak, V. M., 2008. A system of monitoring and control for storage of nuclear materials. In: Modeling and Information Technologies. Institute of Modelling in Energy Engineering, Natl. Acad. Sci., Kyiv, Issue 47, P. 107-118 (in Ukrainian).
- Janossy, L., 1965. Theory and Practice of the Evaluation of Measurements, Oxford University Press (464 p. in Russian translation, Mir, Moscow,1968).
- Electronic resource : http://en.wikipedia.org/wiki/Conjugate_prior
- Electronic resource : http://en.wikipedia.org/wiki/Standard_deviation
