В современных технических университетах классические формы проведения занятий (лекции, практические и лабораторные занятия) становятся менее популярными, а с переходом на бакалавриат значительно сократилось количество часов, отводимых на аудиторные занятия. Поэтому на первый план выступает разработка и организация новых форм образовательного процесса, направленных на его интенсификацию, индивидуализацию и развитие творческих способностей будущих специалистов.
Для решения этих задач большое значение при изучении физики имеет модернизация лабораторного практикума и его интенсификация, при сокращении отведенных на него часов, за счет увеличения инновационной составляющей лабораторных работ. Инновационное отличие работы «Проверка законов механики Ньютона с помощью прибора Атвуда» от известных ее модификаций [1,2] заключается в использовании очень точного оптоэлектронного метода измерений и их обработки с помощью компьютерной программы для решения системы линейных уравнений, что позволяет расширить предметные знания студентов по разделу «Классическая механика»
Прибор Атвуда предназначен для изучения механического движения. Принцип работы прибора основан на использовании законов механики Ньютона [3].
Через блок, смонтированный на подшипнике таким образом, чтобы он мог вращаться с возможно малым трением, проходит нить с двумя одинаковыми грузами массой m каждый (рис.1). Если правый груз массой m,находящийся в верхнем положении на высоте ![]() от выбранного нулевого уровня
от выбранного нулевого уровня ![]() (левый груз массой mнаходится на высоте
(левый груз массой mнаходится на высоте ![]() ) и положить на него небольшой груз массой
) и положить на него небольшой груз массой ![]() , то система грузов
, то система грузов ![]() получит ускорение под действием силы тяжести и придет в движение.
получит ускорение под действием силы тяжести и придет в движение.
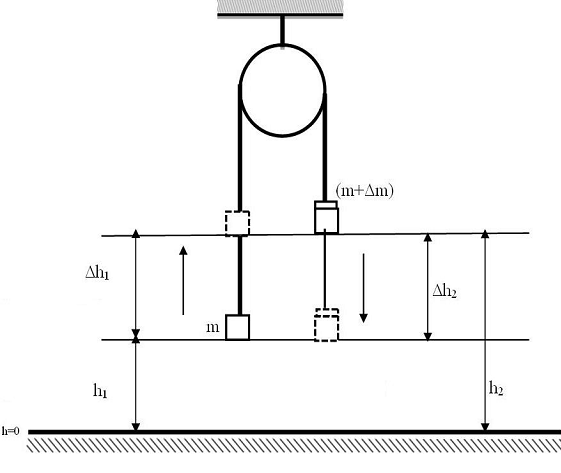
Рисунок 1 – Схема лабораторной установки
В стандартных моделях лабораторных работ, использующих прибор Атвуда [2], как правило, не учитываются:
- сила трения в подшипнике оси блока, которая обычно составляет заметную долю вес перегрузка;
- масса блока и его момент инерции, влияющие на результаты опыта:
- при измерении времени прохождения грузов имеют место достаточно большие случайные и систематические ошибки.
Все эти факторы приводят к тому, что найденные экспериментальные значения ускорения свободного падения находятся в плохом согласии друг с другом и с табличным значением ускорения свободного падения.
Предлагаемый в данной работе метод измерений и их обработки позволяет исключить перечисленные выше недостатки и расширить спектр изучаемых законов механики за счет включения в лабораторную работу закона сохранения энергии и основного закона динамики вращательного движения. В качестве критерия выполнения основных законов механики используется экспериментальное значение ускорения свободного падения и степень его отличия от табличного значения ускорения свободного падения.
Как известно, изменение механической энергии системы тел равно работе неконсервативных сил, приложенных к телам этой системы [4]:
![]() (1)
(1)
где ![]() – конечная, а
– конечная, а ![]() – начальная механическая энергия системы,
– начальная механическая энергия системы, ![]() – работа неконсервативных сил, в данном случае – сил трения в оси блока.
– работа неконсервативных сил, в данном случае – сил трения в оси блока.
В рассматриваемой системе грузы обладают потенциальной энергией силы тяжести: ![]() , где h - высота центра масс тела над выбранным нулевым уровнем, m – масса этого тела, g – ускорение свободного падения.
, где h - высота центра масс тела над выбранным нулевым уровнем, m – масса этого тела, g – ускорение свободного падения.
Кроме того, при поступательном движении грузов у них будет кинетическая энергия 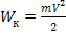 , где
, где ![]() - скорость
- скорость
этого движения, а у блока – кинетическая энергия вращательного движения - 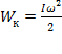 , где
, где ![]() – момент инерции блока при вращении вокруг его оси, а
– момент инерции блока при вращении вокруг его оси, а ![]() – угловая скорость этого вращения.
– угловая скорость этого вращения.
Таким образом, считая, что исходно тела покоились, имеемсм. рисунок 1):
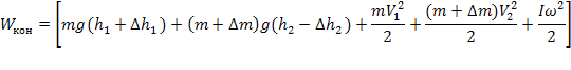
![]()
Подставив эти выражения вормулу, получим:
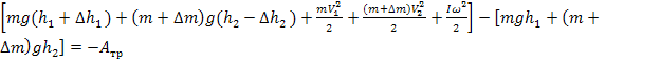 (2)
(2)
( при этом нить считается невесомой и нерастяжимой). Так как нить нерастяжима, то расстояния, пройденные грузами, а следовательно и скорости движения одинаковы: ![]() ,
, ![]() .
.
После алгебраических преобразований получаем:
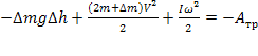 (3)
(3)
Так как нить не проскальзывает по блоку, то угол поворота блока ![]() связан с перемещением нити (и грузов на
связан с перемещением нити (и грузов на
ней) ![]() соотношением:
соотношением: 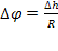 , где
, где ![]() – радиус блока. Поэтому связь угловой скорости
– радиус блока. Поэтому связь угловой скорости ![]() вращения блока и
вращения блока и
линейной скорости грузов на нити ![]() имеет вид:
имеет вид: ![]() .
.
Следовательно, формулу (3) можно переписать в виде:
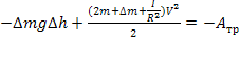 (4)
(4)
Будем считать, что момент силы трения M в оси блока постоянен (в общем случае это неверно, так как сила трения, и, следовательно, момент этой силы зависят от скорости движения). В этом случае работу силы трения при вращении блока можно вычислять по формуле:
![]()
Кроме того, все силы, приложенные к телам системы, будут постоянными, следовательно, движение всех тел будет равноускоренным. Поэтому:
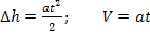
Таким образом, получаем:
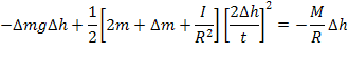
или
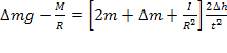
Запишем это уравнение в виде:
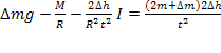 . (5)
. (5)
Если провести измерения времени движения t при трех различных массах дополнительных грузов ![]() , задавая одно и то же перемещение
, задавая одно и то же перемещение ![]() , получим систему из трех уравнений (5). Решив систему уравнений, можно вычислить момент силы трения M в оси блока, момент инерции блока I и ускорение свободного падения g.
, получим систему из трех уравнений (5). Решив систему уравнений, можно вычислить момент силы трения M в оси блока, момент инерции блока I и ускорение свободного падения g.
Для измерения времени движения грузов используется оптоэлектронный датчик, соединенный с электронным процессором, точность определения времени которого составляет 0.001с. Электронный ключ процессора включает электромагнит, грузы приходят в движение, одновременно с этим процессор включает электронный секундомер. Ошибка в определении времени менее 0.1%, точность эксперимента высока.
Для решения системы уравнений с численными коэффициентами применять формулы Крамера нецелесообразно. Поэтому в нашем случае удобно использовать метод Гаусса в виде схемы единственного деления [5]. В данной лабораторной работе расчет величин момента силы трения M в оси блока, момента инерции блока I и экспериментального значения ускорения свободного падения g производится по специально разработанной для данной работы компьютерной программе «Атвуд», основанной на методе Гаусса. Критерием правильности нахождения величин, а также правомерности использования законов механики Ньютона для технических расчетов, можно считать степень совпадения экспериментального и табличного значения ускорения свободного падения.
Использование описанной методики позволяет изменять условия проведения эксперимента, например, проводя опыт с двумя дополнительными грузами, пренебрегая силой трения в блоке, или с одним дополнительным грузом, не учитывая трение и массу блока, используя для расчетов одно и то же уравнение (5). Получив экспериментальное значение ускорения свободного падения g, можно сделать вывод о возможности исключения момента силы трения М в оси блока и момента инерции блока I .
Такая постановка задачи позволяет привлечь к выполнению лабораторной работы несколько микрогрупп студентов, поставив перед ними разные цели исследования, а затем инициировать обсуждение полученных результатов. Студенты учатся работать в микроколлективах, приобретают аналитические умения. При написании отчета по работе они представляют сравнительный анализ результатов, полученных в микрогруппах, и учатся принимать оптимальное решение.
Такой инновационный подход к использованию классических лабораторных работ физического практикума способствует формированию профессиональных компетенций и повышению уровня умений и владений за счет использования современных компьютерных технологий и способов измерений.
Библиографический список
- Руководство к лабораторным занятиям по физике. Под редакцией Л.Л.Гольдина. М: Наука, 1983.
- Portal.fpu.ru/page/portal/www Лабораторная работа М-27 «Определение ускорения свободного падения при помощи машины Атвуда.
- С.Э.Хайкин. Физические основы механики. Издание 3. Издательство Лань, 2008. 768с.
- Т.И.Трофимова. Курс физики. М: Академия, 2007. – 560с.
- М.И.Клиот-Дашинский. Алгебра матриц и векторов. 2-е издание. СПб: Издательство «Лань», 1998. 160с.
