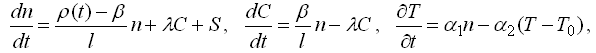Актуальной проблемой современности является развитие атомной энергетики. Ядерный реактор –– сложная техническая система, в которой используются современные достижения автоматики и электроники. В настоящее время любой эксперимент с атомным реактором сначала проигрывается на компьютерной модели: это позволяет безопасно и с малыми затратами исследовать поведение реактора в тех или иных условиях. Методы математического и компьютерного моделирования технических систем подробно рассмотрены в [4 – 6]. В статье обсуждаются учебные варианты компьютерных моделей, позволяющих исследовать функционирование гипотетического ядерного реактора в различных режимах.
1. Постановка задачи
Рассмотрим ядерный реактор –– устройство, в котором протекает управляемая цепная ядерная реакция, сопровождающаяся выделением большого количества энергии (рис. 1). Он состоит из камеры 1, окруженной защитой, в которую помещают ядерное топливо и замедлитель нейтронов. Для управления работой реактора используются стержни 3, вдвигаемые в активную зону 2 с помощью двигателя 4. Через активную зону прокачивается водяной или жидкостный теплоноситель, который поступает в теплообменник, где и передает тепло водяному пару, вращающему паровую турбину. Для контроля интенсивности ядерной реакции используют датчики радиоактивности и температуры 6, подключенные к устройству управления 5, которое включает двигатель, перемещающий управляющие стержни.
В реактор загружают ядерное топливо так, чтобы его масса превысила критическое значение. Начинается цепная ядерная реакция: в результате поглощения нейтрона ядром урана и его деления на осколки в среднем образуется K = 2,5 нейтронов. После деления ядра 99 процентов нейтронов появляются сразу же –– это мгновенные нейтроны. Остальные испускаются через некоторое время (10 – 50 c) после 1 – 2 актов бета–распадов получившихся осколков деления. Часть из них поглощается управляющими стержнями, а оставшиеся захватываются ядрами и вызывают их деление. Чтобы уменьшить интенсивность ядерной реакции, в активную зону вводят управляющие стержни, поглощающие нейтроны [1, c. 336–340]. Типичная нестационарная задача реакторной физики состоит в расчете пуска, увеличения мощности и остановки ядерного реактора.
2. Модель сферического ядерного реактора, учитывающая диффузию нейтронов и теплопроводность среды
Рассмотрим сферический ядерный реактор (рис. 1.2), состоящий из ядерного топлива 1, защиты 2 и управляющих стержней 3. Модель должна учитывать образование нейтронов в результате ядерного распада, их диффузию и теплопроводность среды [2, 3, 7]. Запишем соответствующие уравнения в сферических координатах: 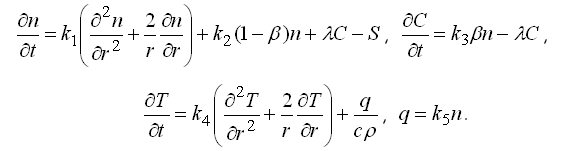
В устройство управления заложена программа запуска, разгона и остановки реактора, а также регулирующая функция, связывающая напряжение U на выходе датчика с усилием F, создаваемым двигателем. Каждый управляющий стержень имеет массу m и соединен с демпфером, который необходим для затухания возникающих колебаний. Уравнение движения управляющих стержней имеет вид: , где r – коэффициент сопротивления. Увеличение x приводит к росту доли нейтронов, поглощаемых управляющими стержнями. Регулирующая функция, связывающая усилие двигателя с напряжением U на выходе датчика, имеет вид:
. Здесь U_0 – заданное значение напряжения, а разность
пропорциональна быстроте изменения напряжения U. Первое слагаемое учитывает отклонение наблюдаемого U от заданного уровня U_0, а второе слагаемое –– быстроту изменения U. Когда U превышает U_0 и/или быстро растет, двигатель действует на систему стержней с силой F, вдвигая их в активную зону на расстояние x. Для шарового реактора поглощающая способность материала с ростом расстояния r до центра O убывает обратно пропорционально квадрату r, поэтому
.
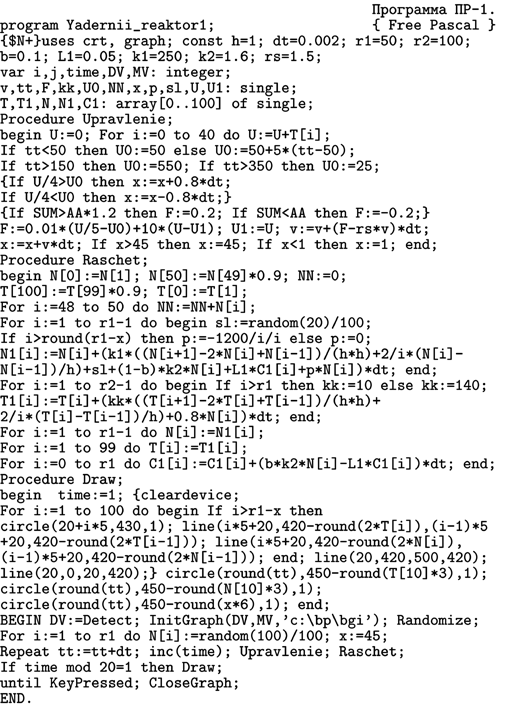
При заданных параметрах реактора подберем регулирующую функцию F(U) и зависимость U_0(t), при которых он плавно входит в рабочий режим, увеличивает свою мощность до некоторого значения, а затем останавливается. Используемая программа ПР–1 содержит цикл по времени, в котором рассчитываются концентрация нейтронов n, число ядер предшественников C и температура T (процедура Raschet), определяется напряжение на выходе датчика и глубина x погружения стержня (процедура Upravlenie), результаты выводятся на экран (процедура Draw). При этом регулирующая функция имеет вид: F(t)=0.01(U(t)/5-U_0)+10(U(t)-U(t-1)), а зависимость напряжения U_0 от времени может быть задана так, чтобы избежать резких “всплесков радиоактивности”. Все величины измеряются в условных единицах.
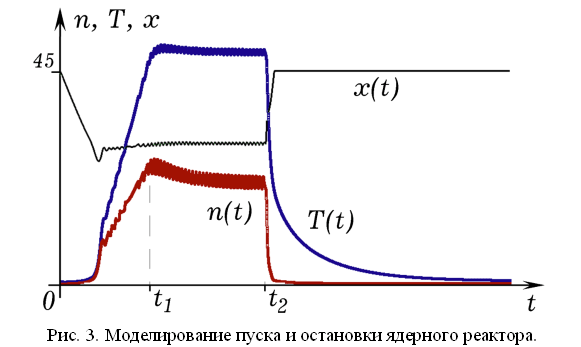
Можно убедиться, что при таком задании управляющей функции F(U) и зависимости U_0(t) интенсивность “ядерной реакции” изменяется плавно, “реактор” работает без резких всплесков уровня “радиоактивности”. На рис. 2 представлены графики распределения нейтронов n(r) и температуры T(r) в процессе работы реактора в различные моменты времени. Графики зависимостей n(t), T(t) и x(t) при пуске, работе и остановке реактора показаны на рис. 3. Видно, что в установившемся режиме система находится в динамическом равновесии, управляющие стержни, а с ними концентрация нейтронов n и температура T, колеблются с небольшой амплитудой. В момент t_2 заданный уровень U_0 падает до нуля, стержни погружаются на максимальную глубину, ядерная реакция быстро затухает, температура понижается до температуры среды. Если управляющая функция F(U) не будет зависеть от скорости изменения U (например, F(t)=0,01*(U(t)/5–U_0)), то при запуске “реактора” происходит быстрый рост “радиоактивности”.
3. Точечная модель реактора (упрощенный вариант)
Пренебрежем размерами реактора и будем считать, что его состояние определяется набором единых осредненных величин (концентрация нейтронов и температура). При этом мы не учитываем диффузию нейтронов, неоднородное нагреванием активной зоны и создаем точечную модель ядерного реактора.
Начнем с простых рассуждений. За единицу времени возьмем время, требуемое для появления нового поколения нейтронов (обычно несколько минут). Пусть в момент t = 0 в реакторе N = 10 нейтронов. Нейтроны поглощаются ядрами, те распадаются, появляется новое поколение нейтронов. Коэффициент размножения нейтронов равен K=2,4, то есть в момент t = 1 появляется N_1=K*N нейтронов, в момент t = 2 появляется N_2=K*N_1 нейтронов и т.д. Долю нейтронов, вылетающих в окружающую среду, обозначим через p_1; долю нейтронов, поглощаемых управляющими стержнями –– через p_2. Тогда за время dt dN=p_1*N*dt нейтронов вылетает в окружающую среду, а dN_2=p_2*N*dt нейтронов поглощается стержнями. Оставшиеся dN_3=N*(1–p_1–p_2)*dt нейтронов захватываются ядрами, вызывают их деление, в результате чего появляется следующее поколение нейтронов и выделяется энергия dE= E_1*dN_3 и выделяется мощность P = dE/dt.
Датчики радиоактивности реагируют на изменение числа вылетающих из реактора элементарных частиц, на выходе получается напряжение U=k_1*N_1. Датчик температуры отслеживает температуру теплоносителя, прокачиваемого через активную зону, на его выходе получается напряжение, пропорциональное средней температуре в центральной части активной зоны: U=k_2*T.
Программа ПР – 2, моделирующая работу реактора, содержит цикл по времени с шагом dt = 0.01, в котором вычисляются количество нейтронов dN_1, вылетевших из реактора, число нейтронов dN_2, поглощенных управляющими стержнями, число нейтронов dN_3, захваченных ядрами и вызвавших их деление, вырабатываемая мощность P, напряжение на выходе датчиков U, усилие двигателя F. Это позволяет рассчитать смещение x управляющих стержней (a и v – их ускорение и скорость):
Один раз за 1/dt=100 циклов (то есть с шагом 1) моделируется появление нового поколения нейтронов численностью N(t+dt). Результаты вычислений выводятся на экран в виде графиков зависимостей P(t) и x(t).
Промоделируем пуск ядерного реактора, плавное увеличение его мощности до заданного уровня и остановку. Пусть сначала ядерное топливо не загружено в реактор; оно разделено на части, доля p_1 нейтронов, вылетающих в окружающую среду, велика. Ядерное топливо загружают в реактор (p_1 плавно уменьшается по закону p_1=0,2exp(–0,25*t)), стержни максимально вдвинуты в активную зону (p_2=0,7). Как задан закон изменения U_0(t), ясно из программы ПР–2.
Результаты моделирования представлены на рис. 4. Сначала происходят колебания радиоактивности, обусловленные пуском реактора, затем число образующихся нейтронов практически равномерно возрастает до тех пор, пока реактор не войдет в рабочий режим. В течение интервала [t_3; t_4] реактор выдает постоянную мощность, а начиная с t_4, его мощность равномерно уменьшается, и реактор останавливается. На графиках видно, как колеблются управляющие стержни при запуске реактора, и как они вдвигаются в активную зону при его остановке. Сначала стержни вдвинуты, доля поглощаемых ими нейтронов максимальна и равна p_2=0,7. После t_1 они начинают выдвигаться, p_2 уменьшается, это приводит к запуску реактора: имеет место всплеск радиоактивности и вырабатываемой энергии. Стержни быстро вдвигаются, p_2 растет, возникающие колебания быстро затухают, переходный процесс заканчивается, система входит в установившийся режим. Изменяя коэффициенты в регулировочной функции F(U), можно убедиться, что реактор далеко не всегда ведет себя устойчиво: при некоторых a и b резко увеличивается число появляющихся нейтронов и вырабатываемая энергия, цепная реакция становится неуправляемой.
Компьютерная модель позволяет изучить ситуацию, когда после перехода реактора в установившийся режим происходит резкий всплеск радиоактивности, например, из–за того, что количество нейтронов на небольшое время увеличивается на 10 процентов, а затем возвращается к прежнему значению. На получающихся графиках видно, как реагирует система. Происходит переходный процесс, управляющие стержни, совершив несколько колебаний, останавливаются, система возвращается в состояние динамического равновесия. Понятно, что при слишком сильном увеличении количества нейтронов система выходит из равновесия, реакция становится неуправляемой, происходит ядерный взрыв.
4. Решение системы диффуравнений для точечной модели ядерного реактора
Процессы, происходящие в ядерном реакторе, можно описать следующей системой дифференциальных уравнений [2, 3, 7]:
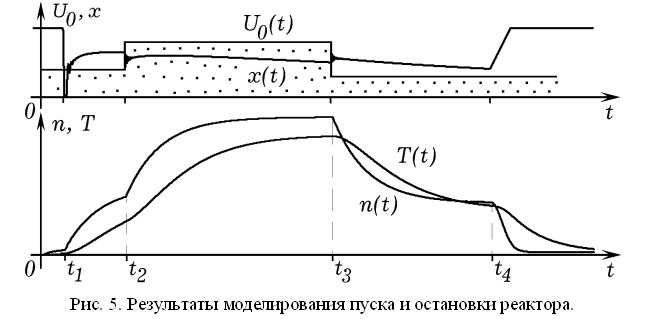
На рис. 5 приведены результаты моделирования работы реактора, управляемого по уровню радиоактивности (программа ПР–3). Модель также позволяет проанализировать различные способы пуска ядерного реактора, и убедиться в том, что при резком изменении интенсивности ядерной реакции в небольших пределах система ведет себя устойчиво.
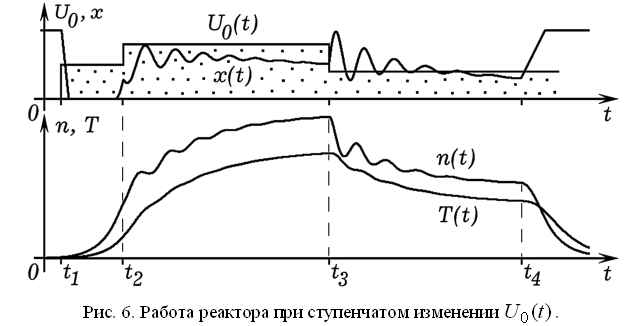
Промоделируем работу ядерного реактора, управление которым осуществляется по температуре теплоносителя при ступенчатом изменении U_0(t) (рис. 6). Для этого в программу ПР–3 следует внести небольшие изменения. Видно, что глубина погружения стержней при резком изменении U_0 совершает затухающие колебания. В момент t_4 управляющие стержни начинают погружаться, ядерная реакция прекращается. На рис. 7 представлены результаты моделирования работы реактора при плавном повышении U_0. Программа позволяет промоделировать аварийную ситуацию, когда интенсивность ядерной реакции, пропорциональная n, резко возрастает. Система автоматически реагирует и снова входит в нормальный режим. Понятно, что рассмотренные выше модели очень приблизительны и представляют интерес только для обучения.
Библиографический список
- Акоста В. и др. Основы современной физики / В. Акоста, К. Кован, Б. Грэм; Пер. с англ. –– М.: Просвещение, 1981. –– 495 с.
- Бартоломей Г.Г. Основы теории и методы расчета ядерных энергетических реакторов: Учеб пособие для вузов / Г.Г.Бартоломей, Г.А.Бать, В.Д.Байбаков, М.С.Алхутов –– М.: Энергоиздат, 1982. –– 512 с.
- Ганев И.Х. Физика и расчет реактора: Учеб. пособие для вузов. –– М.: Энергоатомиздат, 1992. –– 496 с.
- Майер Р.В. Задачи, алгоритмы, программы [Электронный ресурс] / URL: http://mayer.hop.ru (http://maier-rv.glazov.net)
- Неймарк Ю.И. Математические модели в естествознании и технике: Учебник. – Н. Новгород: Издательство Нижегородского госуниверситета, 2004. – 401 с.
- Тарасик В.П. Математическое моделирование технических систем: Учебник для вузов. –– Мн.: ДизайнПРО, 2004 –– 640 с.
- Хетрик Д. Динамика ядерных реакторов –– М.: Атомиздат, 1975. – 400 с.