В настоящее время, задача выбора продуктов-аналогов стоит достаточно остро. На рынке действует огромное количество «игроков», часто, с большим выбором продуктов. Чаще всего, при выборе продукта-аналога, лицо принимающее решение ЛПР руководствуется экспертным методом. Но достаточно ли точен такой метод, ведь он подвластен полностью человеческому фактору? А что если обратиться при выборе к математическим точным методам? Одним из них является вейвлет-анализ.
Вейвлет-анализ является частным случаем спектрального анализа [1].
Смысл спектрального анализа в следующем: Допустим, нам нужно определить, еще не зная будущих потребностей потребителя, в какой момент следует внедрить улучшающую инновацию . У нас есть жизненные циклы (далее ЖЦ) продуктов-аналогов. Пусть нам, так или иначе, удалось получить график зависимости ЖЦ продуктов-аналогов от времени. То есть, как менялась сила потребности во времени. Вообще говоря, ЖЦ по своей физической природе – это волна, то есть колебание определенной среды.
Каждая волна имеет свои параметры, главные из которых – это амплитуда (сила колебания) и частота (насколько быстро меняется состояние среды в данной точке).
Очевидно, что на каждый момент времени может попадать очень много ЖЦ волн разной амплитуды и частоты, такие волны можно распознавать как по амплитуде (силе), так и по частоте. Строго говоря, в каждый момент времени происходит наложение большого количества волн ЖЦ продуктов – аналогов, очень сложно определить, где будет экстремальное значение определенного ЖЦ, а, соответственно, и определить время оптимального ввода улучшающей или замещающей инновации очень сложно (Рисунок 1).
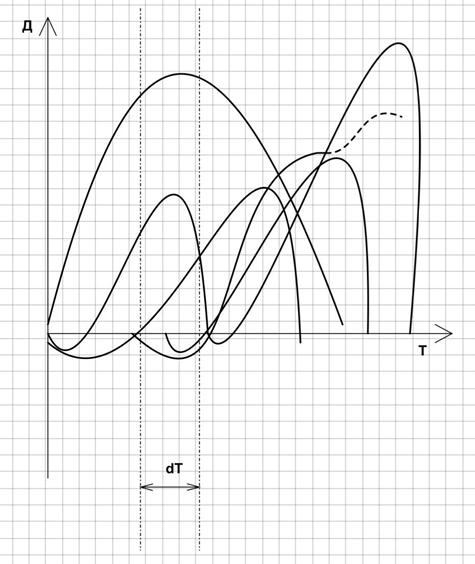
Рисунок 1 – Структурная схема ЖЦ продуктов-аналогов отрасли.
Задача менеджера-инноватора заключается, в первую очередь, в определении значения экстремума каждой волны ЖЦ. То есть он должен так воспроизвести ЖЦ инновционного продукта, чтобы он как можно ближе был по экстремуму к ЖЦ продукта-аналога. Экономическое чутье, тогда по-сути – это способность человека точно назвать частоту определенного ЖЦ продукта. Различить два разных ЖЦ может практически любой человек, а вот точно назвать частоту (экстремум) определенного ЖЦ может не каждый. То есть наша задача узнать, не имея определенных данных будут ли совпадение ЖЦ продуктов-аналогов и ЖЦ инновационного продукта с преобладающей частотой.
Итак, что мы имеем: картину изменения силы ЖЦ продуктов-аналогов, также мы знаем, что график представляет собой сумму большего числа наложившихся друг на друга волн ЖЦ. Если бы нам удалось представить этот график в виде суммы волн различной частоты и амплитуды и если бы на протяжении всего графика все ЖЦ были с одинаковой силой, то мы бы могли ответить на вопрос – когда вводить инновацию. Действительно, если бы выяснилось, например, что график состоит из трех волн ЖЦ, разной частоты, амплитуда двух из которых в 10 раз меньше, чем третьей, то можно с уверенностью заявлять – что это и есть продукт-аналог. Ну а если все три волны имеют примерно одинаковую амплитуду, но сильно разную частоту, то продукта-аналога не существует.
Задача представления ЖЦ в виде суммы “чистых волн” – синусойд (косинусоид) определенной частоты и амплитуды, с целью получения информации о том, на каких частотах наибольшие (наименьшие) амплитуды и называется спектральным анализом. Это умеет делать и наш мозг, только, как и всегда, лишь ему ведомым способом. Однако задача представления функции в виде суммы других функций давно волновала математиков и они придумали точный способ разложения в ряд по синусойдам – преобразование Фурье, при чем доказали, что такое разложение для данного сигнала единственно [2]. Таким образом, применив преобразование Фурье к графику различных волн ЖЦ продуктов-аналогов мы можем объективно судить о принадлежности волны ЖЦ инновационного продукта к определенному типу волн ЖЦ продуктов-аналогов. Получить график несложно – нужно лишь мерить силу потребностей в довольно маленькие промежутки времени. С этой задачей успешно справляется любой маркетолог.
А что теперь, если в течении времени регистрации на графике имеется огромное количество различных волн ЖЦ продуктов-аналогов и инновационных продуктов? Если теперь к такому графику применить преобразование Фурье – то мы получим информацию о том, какие типы ЖЦ продуктов есть на графике (их амплитуды будут самыми большими), однако информацию, о моментах времени, в которые происходит экстремум каждой из волн ЖЦ, а соответственно и в какой момент надо внедрять инновацию мы не получим. Вейвлет-преобразование решает эту проблему (так называемую проблему временной локализации).
Итак, с типами ЖЦ разобрались. Произвели преобразование Фурье графика ЖЦ продуктов-аналогов, и получили, что в его спектре преобладают волны определенных частот, соответствующих известным типам ЖЦ. Чем отчетливей максимумы на графике (это график, только теперь вместо оси времени частота, а по оси амплитуды – соответствующая этой частоте амплитуда), тем четче можно определить тип ЖЦ данного продукта.
Теперь поставим задачу определить правильность момента внедрения инновации. Но спектрограмма (результат преобразования Фурье) не дает никакой информации о том, когда же по времени имели место экстремумы ЖЦ. Потому что преобразование Фурье, примененное к какому либо временному диапазону позволяет судить о частотах, присутствовавших на этом временном диапазоне, но не дает никакой информации о том, в какие именно моменты этого диапазона присутствовала та или иная волна. Конечно, если на всем этом временном диапазоне рассматривать только один ЖЦ одного продукта-аналога, то такая задача не стоит. Есть вариант следующий: для того, чтобы решить нашу задачу, то есть определить, в какой момент времени действует экстремум той или иной волн ЖЦ продуктов-аналогов и инновационных продуктов, нужно лишь разбить график на небольшие участки, в пределах которых (так как они небольшие) можно считать, что действует лишь один определенный тип ЖЦ, а потом просто применить преобразование Фурье к каждому такому участку в отдельности. Таким образом, мы получим спектрограмму для каждого такого участочка и можем определить, когда внедрять ту или иную инновацию. Такая операция с волнами, когда преобразованию подвергаются лишь его участки с целью выявить временное расположение (локализацию) частот называется оконным преобразованием Фурье [3]. Кажется, что проблема решена, она действительно решена, но существует ряд неудобств. Во-первых, таким образом получается не одна спектрограмма (для всего рынка), а набор спектрограмм для определенных ее участков, что не очень удобно. Во-вторых, нужно как то выбирать ширину этих участков – окон (в пределах которых спектральный состав волны не должен изменятся). Если брать слишком большой участок – то, за его длительность может попасться несколько ЖЦ товаров-аналогов, изменив, тем самым, весь спектральный состав, и мы опять не сможем точно сказать в какой момент времени уже внутри этого маленького участка был экстремум определенной волны ЖЦ. Кажется, что если брать слишком маленький участок – то удастся избежать всех проблем. Внутри достаточно малого участка состав если и будет меняться, то незначительно – и если брать бесконечно малый участок – то мы точно получим в какой момент времени экстремум какого ЖЦ был. Однако это нет так и вот чем дело. Чтобы преобразование Фурье “почувствовало” на каком либо интервале времени синусойду, нужно, чтобы этот интервал времени был не меньше периода этой синусойды. То есть, если даже у нас весь рынок состоит из одной-единственной синусоиды, то есть только одного инновационного товара, то преобразование Фурье покажет это, если только в интервал времени, на котором преобразование Фурье осуществляется, войдет, как минимум, один ее период. То есть бесконечно малый интервал времени может “уловить” лишь синусоиду бесконечно малого периода. Очевидно, что чем выше частота (меньше период) волны, тем на меньшем участке времени она может быть выявлена Фурье-преобразованием. То есть чем меньше интервал времени преобразования, чем уже “окно”, тем менее расплывчато во временном отношении мы будем знать о характере сигнала, но тем больше будет тех волн (особенно малой частоты и большого периода), период которых не уложится в этот маленький участок, и преобразование Фурье этого участка времени их не выявит, то есть тем более расплывчато мы будем знать о характере ЖЦ в частотном плане. То есть уменьшая “окно”, мы будем улучшать разрешение во временной области и уменьшать его в частотной. То есть оптимальный размер окна зависит и от самого ЖЦ – если в нем присутствуют низкие частоты – то окно надо выбирать шире, если высокие – уже. Напомню, что спектральный анализ, рассмотренный выше, заключался в разложении ЖЦ по гармоническим функциям (синусам и косинусам). И именно этим объясняется отсутствие временной локализованности преобразования Фурье. Ведь и синус и косинус никакого максимума во временной области не имеют – они там идут бесконечно долго и однообразно. Следовательно и преобразование, в основе которого лежат эти функции эффективны только лишь для таких ЖЦ – которые также монотонно и однообразно идут во времени. В случае же изменяющихся по спектральному составу ЖЦ точно сказать, когда же были эти изменения, как показано выше, обыкновенному преобразованию Фурье не удается. Несколько решает проблему оконное преобразование Фурье, но ему присущи некоторые, отмеченные выше, неудобства. В частности – размер оптимального “окна” зависит от частоты анализируемого ЖЦ. Эти неудобства позволяют избежать разложения по другим функциям, которые, в отличии от синусов и косинусов, имеют максимум (локализованы) во временной области. Если разлагать в ряд по этим функциям, то получается, что оптимальное “окно”, как бы уже становится заложенным “внутри”. То есть эффективность такого преобразования в задаче частнотно-временной локализации (когда нужно узнать не только спектр, но и его характер в различные моменты времени) будет близка к оконному преобразованию Фурье, ширина которого изменяется автоматически в зависимости от рассматриваемой частоты.
Возвращаясь к задаче о ЖЦИ можно сказать, что, разложив график в ряд не по синусам, а по вейвлетам, можно получить спектральное представление ЖЦ в любой момент времени, как если бы мы провели над графиком оконное преобразование Фурье с оптимальными окнами.
Библиографический список
- Новиков Л.В. Основы вейвлет-анализа сигналов // Учебное пособие // Санкт-Петербург. 1999
- Короновский А.А., Храмов А.Е. Непрерывный вейвлет-анализ и его приложения // Саратов: Изд-во ГосУНЦ “Колледж”. 2002. – 216 с.: илл.
- Воробьев В.П., Грибунин В.Г. Теория и практика вейвлет-преобразования //Военный Университет Связи.1999
