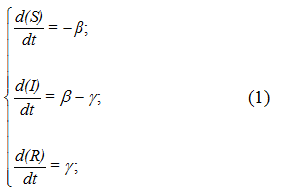Одним из важных приложений методов имитационного моделирования является прогнозирование распространения эпидемических заболеваний. В этой области находят применение системно-динамический.
Системно-динамические (СД) модели распространения эпидемических заболеваний имеют взаимодополняющие свойства, в связи с чем, задача совместного использования этих классов моделей для прогнозирования динамики эпидемических систем является актуальной и требует всестороннего сравнения их характеристик и свойств [1,2].
В качестве примера рассматривались реализации простой SIR модели распространения эпидемического заболевания – гриппа, в среде имитационного моделирования Anylogic версии 5.
AnyLogic поддерживает разработку и моделирование систем обратной связи (диаграммы потоков и накопителей, правила решений, включая массивы переменных). Разработанная модель в среде AnyLogic предназначена для исследования характеристик эпидемии и процесса восстановления системы. Среда позволяет изменять значения параметров модели непосредственно во время ее работы, что в жизни аналогично вмешательству человека в различные процессы.
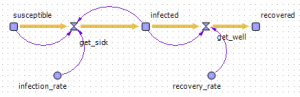
На рис.1 представлена структура системно-динамическая SIR модель распространения гриппа [3].
Рис.1. Структура системно-динамической модели распространения эпидемии.
В модели обозначены: Susceptible (S) – здоровые люди, восприимчивые к гриппу, Infected (I) – инфекционные больные, Recovered (R) – переболевшие гриппом люди, более к нему не восприимчивые, get_sick (β) – доля заразных больных в единицу времени среди инфицированных людей, get_well (γ) – доля выздоровлений в единицу времени среди восприимчивых людей, N – общее число людей.
На рис.1 представлена динамика модели, структура которой, описывается следующей системой алгебро-дифференциальных уравнений (1):
Предположение, что есть постоянное число людей в структуре населения, вытекает следующее простое уравнение:
S(t)+I(t)+R(t)=N(t),
где N = N (t) от общего числа населения. Отметим, что темпы роста инфицированных дается = a/b. Во-первых, мы начнем с уравнения:
S(0)+I(0)=N(0).
Это означает, что оно верно dS/dt<0 когда есть люди, которые инфицированы и те, которые были инфицированы. Так как S уменьшается с течением времени:
S(t)<S(<S(0), для t>>0
значение S постоянно снижается и S должны быть неотрицательными, это означает, что при t→∞, S должна иметь порог, который может быть 0, т. е. 
Из второго уравнения имеем dI/dt < 0, при условии, что как aS < b. Так как S уменьшается, время проходит, следует, что при aS(0) < b и dI/dt < 0 для каждого t> 0, подразумевая, что в этом случае эпидемия исчезает. Там не будет эпидемия, если критическое значение, b/a, достигается начальная популяция неинфицированных. Эта величина мала, если b<<а, это значит, что иммунитет останавливает распространение болезни.
Число выздоровел, R = R(t), из третьего уравнения, монотонно возрастает, но так как 
, предел 
, существует. Далее, предел 
, также существует, а выражение (I (∞) – R (∞) / N) показывает силу эпидемии, которая осуществляется населением. Теперь необходимо определить эти пределы.
Начальные значения параметров эксперимента: N =1000 ; S = N – 1; I = 1; β =0.00218; γ =0.5; τ = 15.
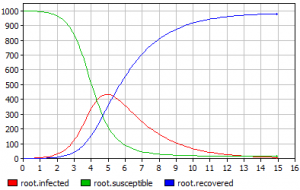
На рисунке 2 представлены результаты эксперимента по имитации распространения эпидемии.
Рис.2 Результаты эксперимента с СД-моделью.
Таким образом, системная динамика является превосходным инструментом для реализации имитационных моделей для распространения эпидемического заболевания. SIR-модель учитывает процесс вывода заражённых субъектов из компьютерной системы. Она базируется на предположении, что во время эпидемии некоторое количество заражённых субъектов либо избавляется от вредоносной программы.
С помощью изоляции зараженных субъектов (исключение восприимчивых узлов из сети на время распространения вредоносной программы) и применения более эффективных средств восстановления зараженных субъектов можно сгладить кривую зараженных (получить меньший пик числа зараженных), с помощью последнего метода также можно сократить время эпидемии.
Библиографический список
- Скворцов А.В., Масленников Б.И. Математическое обеспечение медицинской информационной системы Программные продукты и системы, Международное научно-практическое приложение к международному журналу «Проблемы теории и практики управления» № 4 2008 г. c158-160.
- Д. Ю. Каталевский. Основы имитационного моделирования и системного анализа в управлении, 2011.
- Карпов Ю. Имитационное моделирование систем. Введение в моделирование с AnyLogic 5. – СПб.: БХВ-Петербург, 2006. – 400 с
Количество просмотров публикации: Please wait