Истина бытия – это сущность,
истина сущности есть понятие.
Гегель
ВВЕДЕНИЕ
Понятие «дивергенция» переводится на русский язык как расходимость (можно к этому отнести и сходимость) линий векторного поля. Логически это понятно, в пространственно неоднородном векторном поле (когда есть изменение плотности линий поля) дивергенция не нулевая. В однородном векторном поле дивергенция равна нулю.
На практике, если брать математическое определение дивергенции, то ненулевое значение дивергенции приписывается исключительно только в истоках и стоках поля без определенности их размера. Например, для центральных полей типа электрического и гравитационного, дивергенция считается равной нулю всюду, кроме истоков и стоков. Если же брать в качестве примера магнитное поле, то равенство нулю дивергенции вектора магнитной индукции B вообще возведено в закон (четвертое уравнение Максвелла).
Автор считает, что с точки зрения логики и здравого физического смысла дивергенция в любой точке векторного поля – это скорость пространственного изменения вектора в своем собственном направлении (изменение модуля), а смысл ротора – скорость пространственного изменения направления вектора. Поскольку выделенная в тексте позиция не соответствует общепринятой точке зрения, попробуем пояснить и защитить ее, привлекая наглядные изображения векторных полей, логику понятий и математический аппарат.
ОСНОВНАЯ ЧАСТЬ
Хорошо известны изображения расходящихся и сходящихся силовых линий полей центрального типа (рис.1) и вихреобразных силовых линий стержневого магнита (рис.2). Силовые линии поля строятся по касательным, определяющим направление силы в любой точке пространства, окружающего электрический заряд или магнит.
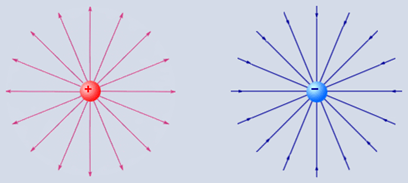
Рис.1 Пространственная расходимость и сходимость линий электрического поля
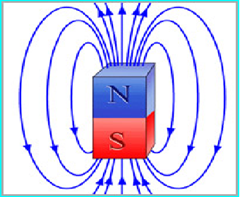
Рис.2. Пространственная расходимость и сходимость силовых линий магнитного поля
Известно, что густота силовых линий определяет числовое значение вектора в любой точке поля, а его направление определяется по касательной к линии в этой точке.
По рис.1, хотя пространственная расходимость и сходимость силовых линий электрического поля очевидны и густота линий убывает при отдалении от центра, дивергенция таких полей (центрального типа) всюду вне источника или стока считается равной нулю.
По рис.2 ситуация сложнее. Считается, что источников магнитного поля нет и линии поля замкнуты сами на себя. В соответствии с четвертым уравнением Максвелла дивергенция силового вектора магнитной индукции B всюду равна нулю. Однако приводимая картина наглядно иллюстрирует, что значение индукции B, определяемое густотой линий, вблизи торцов магнита максимально большое, а в отдалении оно становится меньше. На бесконечно большом удалении от магнита значение магнитной индукции будет нулевым. Таким образом можем констатировать, что в окружающем магнит пространстве тоже имеет место изменение модуля вектора B – это эмпирический факт.
Но если есть изменение модуля вектора (хотя сам поток не изменяется 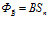 ), то неизбежно будет и дивергенция вектора (или поля, если дивергенцию понимать как пространственную расходимость или сходимость линий поля). Поэтому утверждение четвертого уравнения Максвелла о равенстве нулю дивергенции вектора B в любой точке магнитного поля применительно к рис.2, со всей очевидностью, – ложно.
), то неизбежно будет и дивергенция вектора (или поля, если дивергенцию понимать как пространственную расходимость или сходимость линий поля). Поэтому утверждение четвертого уравнения Максвелла о равенстве нулю дивергенции вектора B в любой точке магнитного поля применительно к рис.2, со всей очевидностью, – ложно.
Несмотря на очевидность приводимых фактов, известных почти каждому, в физике почему-то общепринято и не подвергается сомнению известное положение о нулевом значении дивергенции векторных полей вне источников и стоков поля [1-3]. Заблуждение это, по мнению автора, частью связано с гидродинамической аналогией, а частью с привычкой упрощенного описания центральных полей в сферической системе координат.
Приведем конкретные примеры из классических учебников с имеющейся там трактовкой понятия дивергенции. Возьмем классический учебник Тамма И.Е. «Основы теории электричества» [1, стр.586]. Тамм пишет: «Отметим в заключение, что в гидродинамике дивергенция скорости жидкости v имеет непосредственное физическое значение. Действительно, в каждой точке жидкости
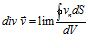 при
при 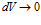 (1)
(1)
равна рассчитанному на единицу объема количеству жидкости, вытекающей из элемента объема dV , окружающего рассматриваемую точку. Название «дивергенция», что значит по-латыни расхождение или расходимость, было избрано для этой величины именно потому, что жидкость растекается или расходится из тех или только тех точек или участков занимаемого ею пространства, в которых div v > 0. Очевидно, что в этих точках должны быть расположены источники жидкости. По аналогии, те точки поля произвольного вектора а, в которых div а
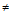 0, принято называть истоками этого поля. Числовое же значение div а называется силой, или обильностью
0, принято называть истоками этого поля. Числовое же значение div а называется силой, или обильностью
истоков поля; в зависимости от знака дивергенции сила истоков может быть как положительной, так и отрицательной. Иногда отрицательным истокам поля дают название стоков поля. Векторные поля, у которых div а = 0, называются свободными от источников, или соленоидальными».
Слова сила или обильность истоков и стоков поля здесь применены правильно, они очень хорошо подходят в качестве характеристики для источников и стоков поля. Но причем тут дивергенция (расходимость) поля?
Другой источник, более современный, описывая дивергенцию конкретного электрического поля [2, стр.24], излагает так: «В дифференциальной форме теорема Гаусса является локальной теоремой: дивергенция поля Е в данной точке зависит только от плотности электрического заряда ρ в этой точке и больше ни от чего. Это одно из замечательных свойств электрического поля. Например, в разных точках поля точечного заряда поле Е отличается друг от друга. Это же относится, вообще говоря, и к пространственным производным 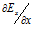 ,
, 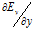 ,
, 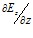 . Однако, как утверждает теорема Гаусса, сумма этих производных, которая определяет дивергенцию Е, оказывается во всех точках поля (вне самого заряда) равной нулю».
. Однако, как утверждает теорема Гаусса, сумма этих производных, которая определяет дивергенцию Е, оказывается во всех точках поля (вне самого заряда) равной нулю».
В этой фразе чувствуются сильные нотки сомнения в излагаемом материале, но они прикрыты ссылкой на авторитет теоремы Гаусса. Но вообще-то защищать позицию, при которой производные по координатам есть, а их сумма всегда равна нулю – это против здравого смысла. Ведь пространственные изменения по трем координатам вполне могут быть одного знака, а также изменение может быть только по одной координате. В последнем случае вообще некуда деваться, ведь при изменении вектора по одной единственной координате, совпадающей с направлением вектора, как ни крути, а придется признавать наличие ненулевой дивергенции.
Наглядная иллюстрация к этому случаю приведена на рис.3. Здесь изображено изменение плотности электрического тока в линейном однородном проводнике переменного сечения. Очевидно, что на участках Б и Г, где происходит переход от одного значения плотности тока к другому значению, 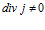 . Аналогичный пример можно привести и для жидкости, текущей в линейной трубе переменного сечения. Для скоростного потока жидкости в трубе, как и для плотности тока, дивергенция потокового вектора в местах расширения и сужения трубы не будет равна нулю – это факт.
. Аналогичный пример можно привести и для жидкости, текущей в линейной трубе переменного сечения. Для скоростного потока жидкости в трубе, как и для плотности тока, дивергенция потокового вектора в местах расширения и сужения трубы не будет равна нулю – это факт.
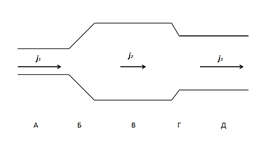
Рис.3. Изменение плотности тока в линейном проводнике переменного сечения
Если рассматривать потенциальное электрическое поле точечных зарядов (рис.1), то ситуация с критикуемым пониманием дивергенции вообще забавная. Вне заряда дивергенция признается равной нулю, а в самом заряде она неопределенна ввиду немыслимо большой плотности заряда. Тогда о каком значении дивергенции вообще можно вести речь?
Приведем еще один пример из зарубежных источников (заблуждение не знает границ) [3, стр.73]. Рассматривается электрическое поле, создаваемое заряженным источником в виде бесконечно длинного цилиндра. «Вне цилиндра, где нет заряда, конечный поток, вытекающий из любого объема – и большого и малого, – равен нулю, так что предел отношения потока к объему, конечно, равен нулю. Внутри цилиндра мы получили результат, следующий из фундаментального соотношения (54) (примеч. в ссылке div E = 4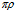 )».
)».
Интересно, как это понимать: «дивергенция внутри цилиндра». Еще более нелепым будет определение дивергенции «внутри» электрона или протона. Если же отойти от слова «внутри», то возникает вопрос – на каком расстоянии от источника или в каком объеме вычислять дивергенцию. Если в расчет брать только размер микрочастиц, то значение дивергенции (и плотности  ) будет чудовищно большим из-за малой величины размера микрочастиц. Так, для отдельного электрона div E = 1,93·1035 В/м2, при этом данная цифра совсем ничего не говорит о пространственной расходимости векторного поля, создаваемого электроном. Значит, здесь что-то не так.
) будет чудовищно большим из-за малой величины размера микрочастиц. Так, для отдельного электрона div E = 1,93·1035 В/м2, при этом данная цифра совсем ничего не говорит о пространственной расходимости векторного поля, создаваемого электроном. Значит, здесь что-то не так.
В этой же книге [3] приводится иллюстрация, изображенная на рис.4, позволяющая трактовать дивергенцию точно так же, как ее понимает автор настоящей статьи.
Выделенная область на рис. 4 б) не содержит источников и стоков, однако дивергенция поля в этой области не равна нулю и это правильно. Дивергенция есть в любой точке неоднородного поля, неоднородного в реальном трехмерном физическом пространстве. То есть в любой точке поля, где наблюдается расходимость или сходимость линий векторного поля.
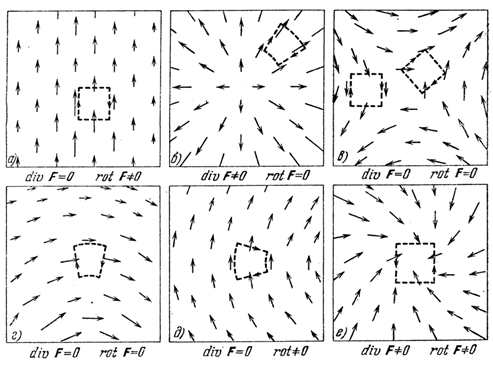
Рис.4. Значения дивергенции и ротора в выделенной области векторного поля
Исходя из описываемого здесь понятия дивергенции, можно предположить, что в случае центрального электрического поля (берем вектор D в системе СИ), дивергенция в любой точке поля будет численно равняться объемной плотности заряда, приходящегося на объем шара с радиусом, равным удалению данной точки поля от центрального источника. В этом случае работают и теорема Гаусса и наше понимание дивергенции векторного поля.
Одним из оппонентов данной точки зрения на дивергенцию автору была высказана претензия в том, что он «придумал» свое определение дивергенции и не вправе пользоваться общепринятым. Помилуйте! Я ничего не придумывал и пользуюсь таким определением, как оно есть [4, стр. 358]. Дивергенцией называется функция
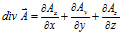 , (2)
, (2)
а то, что она входит в подынтегральное выражение формулы Остроградского
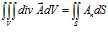 , (3)
, (3)
так эта формула, при допущении равномерной плотности потока, применима для поверхностей и объемов любого размера. При отсутствии такого допущения формулой (3) пользоваться практически невозможно.
Наше понимание дивергенции, как изменения вектора в своем собственном направлении, математически обоснована тем, что формула (2) обязательно дает нулевой результат только при неизменности модуля вектора 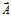 . Это определяется свойством любого вектора – сохранять свое значение по модулю при любых поворотных изменениях системы координат. Заметим, прямо противоположное качество у функции ротора вектора.
. Это определяется свойством любого вектора – сохранять свое значение по модулю при любых поворотных изменениях системы координат. Заметим, прямо противоположное качество у функции ротора вектора.
Осознание ложности привязки понятия дивергенции лишь к источникам и стокам поля уже появилось в гидродинамике [5]. По мнению автора, не за горами признание аналогичного положения и в других областях физики, в частности, в электростатике и магнитостатике. Отмеченное соответствует математическому положению о том, что «всякое векторное поле А дает некоторое скалярное поле divA, а именно поле своей расходимости» [4, стр.359]. Если векторное поле непрерывно и дифференцируемо в своей области, то в той же области должно существовать и быть непрерывным скалярное поле его дивергенции.
К сожалению, большинство математических и физических источников трактуют сегодня понятие дивергенции совершенно иначе. Например [6, пример 7.10, стр.406]: «Силовое поле, создаваемое в пустоте помещенным в начало координат электрическим зарядом q0 , имеет аналогичный вид …, дивергенция рассмотренных силовых полей при 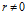 равна нулю». Правда наблюдаются и попытки вынести понятие дивергенции из «прокрустова ложа» истоков и стоков поля. В источнике [7, стр.171] приводится такая формула:
равна нулю». Правда наблюдаются и попытки вынести понятие дивергенции из «прокрустова ложа» истоков и стоков поля. В источнике [7, стр.171] приводится такая формула:
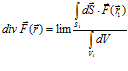 при
при 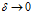 (4)
(4)
где: 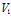 - область, содержащая точку (
- область, содержащая точку (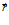 ),
), 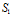 - замкнутая поверхность, ограничивающая область
- замкнутая поверхность, ограничивающая область 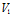 ,
, 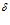 - наибольшее расстояние от точки (
- наибольшее расстояние от точки (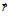 ) до точек поверхности
) до точек поверхности 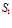 .
.
В формуле (4) имеет место уход от устремления объема в точку, анализируются поверхность и объем, внутри которых расположена рассматриваемая точка поля. При правильной интерпретации этой формулы и применительно к полям центрального типа она дает результат, близкий к верному.
В источнике [8] для физических полей приводится еще одно, несколько иное, определение дивергенции. Здесь дивергенция определяется как показатель объемной плотности потока векторной величины в той или иной точке пространства векторного поля. Дивергенция в этом случае математически выражается так:
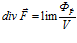 при
при 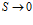 (5)
(5)
где: 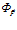 – поток векторного поля
– поток векторного поля 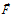 через сферическую поверхность площадью S, ограничивающую объем V. Считается, что такое определение дивергенции применимо не только к декартовым системам координат. Надо отметить, что здесь не очень понятно требование сферичности, а не замкнутости поверхности.
через сферическую поверхность площадью S, ограничивающую объем V. Считается, что такое определение дивергенции применимо не только к декартовым системам координат. Надо отметить, что здесь не очень понятно требование сферичности, а не замкнутости поверхности.
В чем-то аналогичный подход обнаруживается и в работе [9, стр.22]: «… дивергенция векторного поля а(М) является объемной плотностью потока векторного поля а(М) в данной точке М». По мнению автора, такой подход более близок к истине.
В источнике [8] приводится интересный пример наглядной физической модели дивергенции: «Например, если в качестве векторного поля взять совокупность направлений наискорейшего спуска на земной поверхности, то дивергенция покажет местоположение вершин и впадин, причём на вершинах дивергенция будет положительна (направления спуска расходятся от вершин), а на впадинах отрицательная (ко впадинам направления спуска сходятся)».
По мнению автора, такая модель дивергенции не совсем логична. На вершинах и впадинах наискорейшего спуска совсем нет, а в источниках или стоках дивергенция по модулю должна быть максимальна. Кроме того, данная модель, во-первых, исключает гладкость вершин и впадин, поскольку значения дивергенции скачут от плюса к минусу, а правило перехода не обозначено. Во-вторых, надо заметить, принимая пространственное направление за векторную величину, ее нельзя определять в том же пространстве направлений. Пример из логики: нельзя определить понятие через само это понятие, иначе получится тавтология.
В наглядных примерах по рис.1 и рис.2 видно, что дивергенция (расходимость) электрических и магнитных силовых линий есть и заведомо есть плавное уменьшение модуля вектора при отдалении рассматриваемых точек окружающего пространства от источника и стока поля. Для центральных полей вычислить дивергенцию как объемную плотность потока вектора в той или иной точке поля не сложно. Но для соленоидального магнитного поля определение дивергенции как объемной плотности потока векторного поля затруднительно, поскольку это поле не сферично. К тому же заметим, дивергенция, по сути, должна быть не плотностью потока векторного поля, что присуще и однородным векторным полям, а пространственным изменением плотности потока вектора в той или иной точке поля. Математически это можно выразить так:
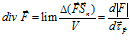 при
при 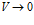 и
и 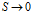
 (6)
(6)
где: 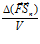 – изменение плотности потока векторной величины
– изменение плотности потока векторной величины 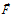 в рассматриваемом объеме
в рассматриваемом объеме 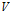 предельно малого размера;
предельно малого размера; 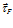 – единичный вектор, касательный к направлению вектора
– единичный вектор, касательный к направлению вектора 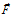 в данной точке.
в данной точке.
Кажется не вполне осознаваемое, но почти полное соответствие авторскому пониманию дивергенции удалось обнаружить в источнике [10, стр.206]: «Дивергенцию векторной функции … еще называют расходимостью. Она определяет скорость изменения каждой компоненты вектора в своем «собственном» направлении». Но если есть изменения компонентов вектора в своем «собственном направлении», то не замечать или отрицать такое же изменение самого вектора – просто грешно.
Обсуждение полученных результатов.
В заключение приведем и рассмотрим для сравнения в табличном формате различные варианты определения дивергенции, в том числе, предлагаемые автором и защищаемые им как наиболее подходящие (см. таблицу 1).
Таблица 1. Возможные определения и толкования дивергенции
| Определение дивергенции |
Математическое определение |
Условие определения |
Физический смысл дивергенции |
| Общепринятое и разделяемое |
автором
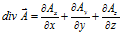
Пространственная производная в точке поля
Пространственная расходимость или сходимость векторного поля
Общепринятое, но не разделяемое автором
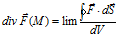
при 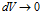
Объемная плотность потока через замкнутую поверхность предельно малого объема
Дивергенция – это истоки и стоки векторного поля
Вариант, встречающийся как возможный
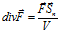
при 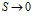 и
и 
Объемная плотность потока при 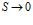 и
и 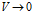
Объемная плотность потока векторного поля
Авторский
вариант 1
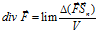
при 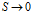 и
и 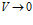
Дивергенция численно равна градиенту объемной плотности потока
Пространственное изменение объемной плотности потока векторной величины
Авторский
вариант 2
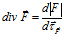
Дивергенция – это изменение модуля вектора
Пространственное изменение векторной величины в ее собственном направлении
Рассмотрим отличия в оценке дивергенции, применительно к вектору 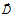 электростатического поля в точке М, находящейся на расстоянии
электростатического поля в точке М, находящейся на расстоянии 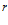 от центрального заряда
от центрального заряда 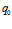 . Общепринятое значение дивергенции вне истоков и стоков поля равно нулю (
. Общепринятое значение дивергенции вне истоков и стоков поля равно нулю (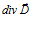 = 0). Значение, вычисленное из условия равномерной объемной плотности заряда, приходящегося на весь рассматриваемый сферический объем, о чем говорилось ранее, как о возможном приблизительном определении дивергенции, составляет:
= 0). Значение, вычисленное из условия равномерной объемной плотности заряда, приходящегося на весь рассматриваемый сферический объем, о чем говорилось ранее, как о возможном приблизительном определении дивергенции, составляет:
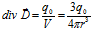 .
.
Авторские варианты определения дивергенции по вариантам 1 и 2, по идее, должны быть эквивалентны. Значение дивергенции по варианту 1:
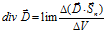 =
= ,
,
а по варианту 2:
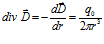 .
.
Критики нашего понимания дивергенции говорят: пусть это даже так и есть, но что это дает нового? Стоит ли из-за этого все учебники переписывать? Ответим так: новое знание о природе никогда не бывает излишним. Ведь устоявшееся представление о дивергенции тоже в чем-то право (математика – это тоже наука). Например, применительно к электрическому полю в точках полевого пространства, в которых дивергенция поля не равна нулю, нужно найти объяснение наличия вполне определенной объемной плотности заряда. И этому есть объяснение, попробуем его сформулировать.
Физическое объяснение отличной от нуля дивергенции в любом месте расходящегося или сходящегося векторного поля с определенными значениями величины и знака можно найти, опираясь на представление о наличии в каждой точке физического пространства объемной плотности виртуальных частиц вакуума [11]. Поскольку виртуальные частицы вакуума появляются и исчезают, как считается, парами, то в случае электрического поля наличие того или иного знака объемной плотности заряда, а также его числовое значение, должны определяться пространственным распределением объемной плотности электрического заряда этих пар. Можно сказать по иному, должны определяться неоднородностью поляризации вакуума или тем, частицы какого знака в виртуальных парах (данного места поля) «живут» несколько дольше, по сравнению со своими напарницами.
Для электрического поля исходной «материальной» [12] векторной физической величиной, к которой применимо понятие дивергенции, является поляризованность. Причем поляризованностью вакуума является известная индукция
электрического поля
D, зачастую
причисляемая к вспомогательным и не существующим величинам. Не исключено существование еще одной «материальной» векторной ФВ электрического поля – электрического векторного потенциала
Ae
, об объективном существовании которого давно и настойчиво говорит и пишет В.В. Сидоренков [13, 14]. Без этой физической величины, видимо, нельзя обойтись при описании в «материальных» параметрах вихревых электрических полей.
Для магнитного поля интенсивность и направление дивергенции, видимо, будет определяться пространственным распределением суммарного магнитного дипольного момента виртуальных частиц и, в конечном счете, объемной плотностью этой векторной величины, которую иначе как намагниченностью вакуума [15] не назовешь.
Выводы
1. Математические и физические толкования дивергенции с приписыванием ей нулевого значения вне истоков и стоков поля не соответствуют реальности. Дивергенция (расходимость – сходимость) силовых линий электрического, магнитного и гравитационного полей, неоднородных в трехмерном физическом пространстве, – это эмпирический факт.
2. Используемые иногда определение дивергенции – как объемной плотности потока векторной величины в той или иной точке поля, близко к сущности понятия дивергенции, но более точно определение дивергенции пространственным изменением этого потока.
3. Наиболее простое и точное толкование дивергенции векторного поля в любой его точке – это скорость пространственного изменения вектора в данной точке поля в своем собственном направлении, то есть по модулю. Данное толкование дивергенции совпадает с математическим определением дивергенции через вектор набла.
Библиографический список
- Тамм И.Е. Основы теории электричества. Учеб. Пособие для вузов. – 11-е изд., испр. и доп. – М.: ФИЗМАТЛИТ, 2003. – 616 с.
- Иродов И.Е. Электромагнетизм. Основные законы. Изд. 4-е испр.– М.: БИНОМ. Лаборатория знаний. 2003. – 320 с.
- Парселл Э. Электричество и магнетизм: Учебное руководство; Пер с англ./Под ред. А.Н. Школьникова и А.О. Вайсберга. – 3-е изд., испр. – М.: Наука, 1983. – (Берклеевский курс физики). – 410 с.
- Смирнов В.И. Курс высшей математики. Том 2. Изд. 19 испр. – М.: НАУКА. 1965.
- Волков П.К. О природе движения жидкости./ Вестник Югорского государственного университета. 2011 г. Выпуск 2 (21). С. 8–28.
- Гаврилова В.Р., Иванова Е.Е., Морозова В.Д. Кратные и криволинейные интегралы. Элементы теории поля. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2003. – 496 с.
- Справочник по математике (для научных работников и инженеров). Г. Корн, Т. Корн. – М.: НАУКА. 1973. 832 с.
- Дивергенция. URL: http://ru.math.wikia.com/wiki/Дивергенция (дата обращения – 10.11.2012).
- Болсун А.И., Гронский В.К., Бейда А.А. Методы математической физики: Учеб. пособие. – Минск.: Высш. шк., 1988. – 199 с.
- Ильин В.А., Садовничий В.А., Сендов Бл.Х. Математический анализ. Продолжение курса. Под ред. А.Н. Тихонова. Бл.Х. М.: Изд. МГУ, 1987. 358 с.
- Смолянский С.А. Вакуумное рождение частиц в сильных электромагнитных полях. // Соросовский образовательный журнал, 2001, № 2, с. 69-75.
- Чуев А.С. Системный подход в физическом образовании инженеров // Наука и образование: электронное научно-техническое издание. – 2012.- № 2.- URL: http://technomag.edu.ru/doc/299700.html (дата обращения: 2.02.2012).
- Сидоренков В.В. Электромагнитный векторный потенциал – это первичное собственное поле частиц микромира. URL: http://www.sciteclibrary.ru/rus/catalog/pages/11702.html (дата обращения: 18.01.2012 г.)
- Сидоренков В.В. Современная система уравнений электродинамики Максвелла – анахроничный фетишь физической науки. URL: http://www.sciteclibrary.ru/rus/catalog/pages/12268.html (дата обращения: 04.10.2012 г.)
- Чуев А.С. Магнитное поле – какие векторы первичны и что мы измеряем?/ Журн. «Законодательная и прикладная метрология». 2012. №5.

Здравствуйте Анатолий Степанович. Я тоже поставил под сомнение утверждение divB=0.
С моими работами вы можете ознакомиться здесь:
https://sites.google.com/site/ringmagneticfield/russian
Если вам интересно- пишите.
С уважением.
Дополнительный материал и разъяснения по этому вопросу можно найти в журнале ЭЛЕКТРО №2 за 2016 год, а так же на моей персональной страничке http://www.bmstu.ru/ps/~chuev. К сожалению я не вижу возможности (или не знаю как) приводить здесь формулы и рисунки.
Дополнительный материал по магнитному полю имеется и здесь: http://web.snauka.ru/issues/2015/07/56905. Евгений Валентинович Ваши работы посмотрел, они мне интересны. Готовлю для Вас предложение о совместной работе по электрическому полю, чувствую Вы намного сильнее меня в математике. В ближайшее время постараюсь свои предложения прислать.
У меня сложности с написанием формул на данном сайте. Если вы не возражаете я буду присылать ответы в pdf формате на ваш email.
По электрическому полю у меня тоже есть работы. Они просто не выложены на моём сайте.
Хорошо, жду Вашей информации в ПДФ по электрическому полю.