Современное общество требует от специалистов умения интегрировать знания из разных областей наук, работать в команде, самостоятельно разрабатывать план реализации проекта.
Под учебно-исследовательским проектом будем понимать деятельность студентов по планированию исследования, главной целью которого является развитие личности; в приобретении исследовательских навыков, развитии исследовательского типа мышления.
При организации учебно – исследовательского проекта «Вступительные экзамены по математике в Оксфорд» студентам необходимо было решить следующие вопросы, представленные в виде плана работы:
-
Определить выбор темы проекта, количество участников проекта и первокурсников в время необходимое для выполнения данного проекта. Выбор темы проекта, обусловлен повышенным интересом студентов том, как их сверстники за границей проходят вступительные испытания, какими будут результаты среди одногруппников, сравнить данные результаты с результатами ЕГЭ по математике. Над данным проектом работала команда из 2-х человек в течение недели.
-
Выяснить проблемы, с которыми могут столкнуться при выполнении данного проекта. Студенты при выполнении данного проекта выделили следующие предполагаемые проблемы, каким образом эффективно организовать поиск информации, как осуществить перевод текста, как решить задания.
-
Распределение обязанностей при самостоятельной работе над проектом. В данном случае возможны следующие варианты: часть группы занимается переводом, а другая часть над решением задач; текст делиться на две части и каждая группа занимается переводом и решением задач.
-
Промежуточное консультирование в течение выполнения всего проекта, может быть реализовано как при личной беседе, так и с использованием Интернет технологий.
-
Обобщение результатов работы каждой подгруппы проекта. Создание презентации проекта с выделением общих моментов и отличий по организации вступительных экзаменов в Англии и России.
-
Проведение тестирования среди одногруппников и сравнение результатов с результатами ЕГЭ по математике, а также выяснить количество студентов которые имеют наивысший балл, которые могли пройти вступительные испытания в Оксфорд. Провести статистическую оценку результатов тестирования.
-
Оценивание данной работы. Подведение итогов.
В данном проекте рассматривали задания прошлых лет вступительного теста по математике в Оксфорд на технические специальности. Вступительный экзамен на инженерные и физические специальности на степень бакалавра сдаются в одном бланке и включают две части: часть A – 11 заданий по математике и часть В-14 заданий по физике, каждая из которых оценивается по 50 марок. Задачи оформляются в бланке заданий и вписываются ответы. Экзамен длиться 1 час. Оригинал вступительного теста и форму экзаменационного бланка на английском языке можно найти на сайте Оксфордского университета [1]
-
Если
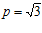 и
и 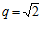 , то значения выражения
, то значения выражения 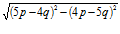 равно… [3 марки]
равно… [3 марки]
Решение. Используя формулы сокращенного умножения раскрываем скобки, приведем подобные, подставим искомые значения.
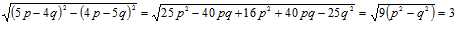 .
.
2. Найти множество действительных чисел λ, для которых квадратное уравнение
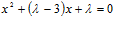 (1) имеет действительные корни х. [4 марки]
(1) имеет действительные корни х. [4 марки]
Решение. Дискриминант уравнения (1) равен
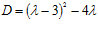 .
.
Корни уравнения
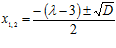 . Корни уравнения (1) будут действительными, если
. Корни уравнения (1) будут действительными, если 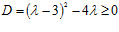 ;
;
Решим уравнение
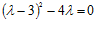 . (2)
. (2)
Раскроем скобки и упростим выражение, получим
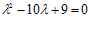 . Корни уравнения (2):
. Корни уравнения (2): 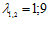 .
.
На числовой оси (рис.1) отметим данные точки и определим знак функции на каждом интервале.
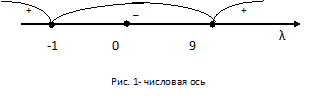
Из рисунка видно, что если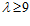 или
или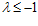 искомое квадратное уравнение (1) имеет действительные корни.
искомое квадратное уравнение (1) имеет действительные корни.
-
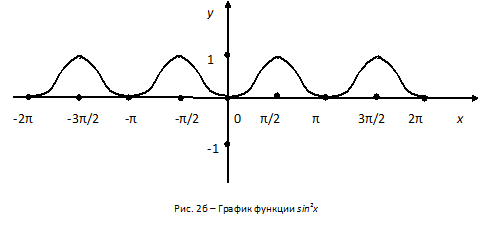
(I) Нарисовать графики функций sinх и sin2x в интервале -2π <x<2π.
[2 марки]
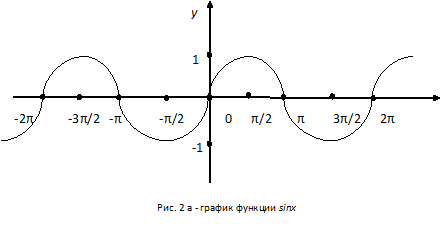 Решение. На рисунке 2а, изображен график функции sinх, на рисунке 2б график функции sin2x.
Решение. На рисунке 2а, изображен график функции sinх, на рисунке 2б график функции sin2x.
(II) Объясните, почему, для интервала от 0 <х < π/2, sinх <tgх. [2 марки]
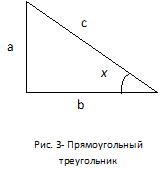
 Решение. Используя соотношения в прямоугольном треугольнике (рис. 3), получим
Решение. Используя соотношения в прямоугольном треугольнике (рис. 3), получим 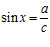 , а
, а 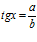 . По теореме Пифагора с2=а2+в2, а из этого следует, что с>b. Значит, sinх< tgx.
. По теореме Пифагора с2=а2+в2, а из этого следует, что с>b. Значит, sinх< tgx.
(III) Используя равенство 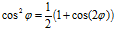 или иным образом, переведите cos4φ в cos(2φ) и cos(4φ). [3 марки]
или иным образом, переведите cos4φ в cos(2φ) и cos(4φ). [3 марки]
Решение.
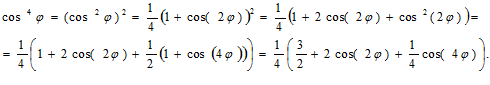
4. Покажите, что точки (3, 4), (-4, 0) и (0, -2) являются вершинами прямоугольного треугольника, и найти его площадь. [5 марок]
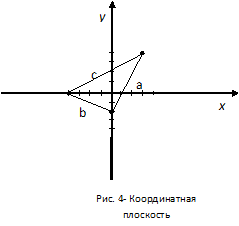 Решение. Изобразим на координатной плоскости (рис.4) искомые точки и убедимся, что они являются вершинами прямоугольного треугольника.
Решение. Изобразим на координатной плоскости (рис.4) искомые точки и убедимся, что они являются вершинами прямоугольного треугольника.
Определим длины сторон треугольника из формулы расстояния между двумя точками: а2=32+(4+2)2=45; b2=42+22=20; с2=(4+3)2+42=65. По теореме Пифагора: с2=а2+в2. Легко можно убедиться, что для сторон данного треугольника, выполняется теорема Пифагора, а значит он прямоугольный. Площадь треугольника: S=0,5ab=15(ед2).
5. Найдите все значения х в следующих равенствах
(I) log2x = 2, [1 марка]
Решение. По определению логарифма х=22=4.
(II) logx2 = 2, [1 марка]
Решение. По определению логарифма х2=2, 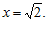
(III) log22 = х. [1 марка]
Решение. По определению логарифма х=1.
6. Оцените значение числа (2,002) 6 с точностью до 4 знаков после запятой. [4 марки]
Решение. Преобразуем данное число (2,002) 6=26(1+0,001)6.
Используя разложение функции в ряд Маклорена 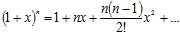
преобразуем выражение (2,002) 6= 64(1+0,001)6=64(1+0,006+15·10-6+…)= 64,38496.
7. Мяч падает вертикально с высоты h на плоскую поверхность. После n
отскоков он поднимается на высоту h/(3n). Найти общее расстояние, пройденное шаром. [4 марки]
Решение. 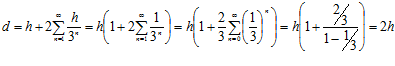 .
.
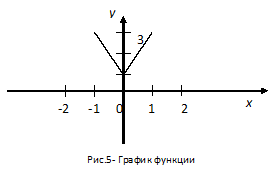 8. (I) Изобразите кривую
8. (I) Изобразите кривую 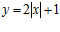 в области -1
в области -1 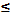 х
х
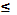 1 [2 марки]
1 [2 марки]
Решение. На рисунке 5 представлен график искомой функции.
(II) Найти площадь между кривой 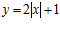 и кривыми х=-1, х=1
и кривыми х=-1, х=1
и осью х. [2 марки]
Решение. На рисунке 6, представлена плоская фигура, образованная пересечением указанных линий.
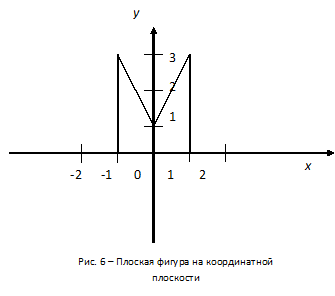
При пересечении искомых кривых получаем 2 одинаковые трапеции. Найдем площадь фигуры 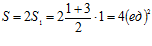 .
.
9. Брошены две игральные кости, один за другим. Каковы вероятности того, что
(I) сумма чисел на игральных костях равна 6. [2 марки]
Решение. Рассмотрим, какие комбинации чисел соответствуют данному условию: 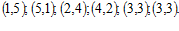 Число всевозможных комбинаций
Число всевозможных комбинаций 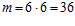 . Определим вероятность данной ситуации
. Определим вероятность данной ситуации 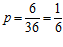 .
.
(II) второе число больше, чем первое? [4 марки]
Решение. В таблице 1 выделили клетки, которые реализуют второе условие. Всего 15 возможных случаев, удовлетворяющих данному условию. Число всевозможных комбинаций 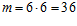 . Определим вероятность данной ситуации
. Определим вероятность данной ситуации 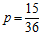 .
.
Таблица 1-Наглядное представление данного условия, для оценки вероятности
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 |
10. Геометрическая и арифметическая прогрессии имеют одинаковые первые члены. Второй и третий члены геометрической прогрессии равны третьим и четвертым членам арифметической прогрессии соответственно.
(I) Найти знаменатель геометрической прогрессии. [2 марки]
Решение. Общий член арифметической прогрессии находится по формуле аn=a1+(n-1)d, а общий член геометрической прогрессии по формуле bn=b1+q(n-1).
По условию: b1=a1; b2=a3; b3=a4. Распишем подробнее данное условие: b2=a3 или a1+2d=b1q. Отсюда, d=(b1q-a1)/2. Распишем условие: b3=a4 или a1+3d=b1q2. Подставим d, в полученное выражение, получим 2q2-3q+1=0. Действительные корни уравнения q=1/2; 1. При q=1, d=0, что противоречит условию, следовательно, знаменатель геометрической прогрессии равен q=1/2.
(II) покажите, что пятый член арифметической прогрессии равен нулю.
[3 марки]
Решение. Пятый член арифметической прогрессии определим из соотношения аn=a1+(n-1)d, или а5=a1+4d. При q=1/2, разность арифметической прогрессии равна d=(b1q- a1)/2=-а/4. Пятый член арифметической прогрессии а5=a1+4d=0.
11. Найти наибольшие и наименьшие значения функции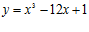 на отрезке от -3 до 5. [5 марок]
на отрезке от -3 до 5. [5 марок]
Решение. Найдем экстремумы функции: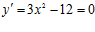 . Корни уравнения
. Корни уравнения 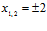 . Найдем значения функции на границе интервала и в экстремальных точках:
. Найдем значения функции на границе интервала и в экстремальных точках: 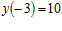 ;
;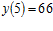 ;
;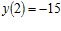 ;
;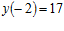 .
.
Следовательно, 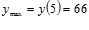 ,
, 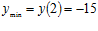 .
.
При выполнении данного проекта выделили следующие отличия и схожесть вступительных тестов по математике в России и Англии:
-
рассогласованность школьных учебных программ по математике. При сдаче экзаменов в Оксфорд российский школьник может обнаружить у себя недостаток знаний по таким разделам математики как алгебра и математический анализ, тригонометрия, аналитическая геометрия, комбинаторика, теория вероятностей, статистика и анализ данных. К примеру, российскому школьнику будет затруднительно выполнить задания 6 и 7;
-
время сдачи вступительного теста в вузы России июль-август, а в Оксфорд октябрь-ноябрь;
-
данный тест проходит, централизовано, как и в России.
В ходе выполнения данного проекта преподаватель решает следующие учебные задачи:
-
обучение поисковым приемам исследовательского мышления;
-
обучение процессу и культуре коллективного обсуждения;
-
формирование культуры самооценки и оценки других участников проекта;
-
формирование культуры публичного выступления, защиты полученных результатов.
Данный учебно-исследовательский проект можно организовать как среди студентов первокурсников, изучающих математику, так и среди будущих абитуриентов. Роль педагога при обучении вспомогательная, координирующая деятельность обучающихся.
Библиографический список
- Вариант вступительного теста на по физике и математике для поступающих на инженерные и физические специальности //http://www2.physics.ox.ac.uk/sites/default/files/Sample-Paper_0.pdf.
