Преобладание микропроцессорных систем управления в современных и перспективных электроприводах позволило увеличить алгоритмические возможности управления благодаря гибкости программного обеспечения. Появилась возможность построения систем электроприводов с широкими возможностями регулирования параметров, диагностики состояния, самонастройки и адаптации. Одной из ключевых задач для построения подобных систем является идентификация электропривода. Идентификация позволяет получить модель электропривода с допустимой для практического применения погрешностью динамики.
Когда известна общая математическая модель объекта, то расчет и построение уточненной модели возможны методами классической теории автоматического управления. На практике современные электропривода часто представляют собой многомассовые системы и имеют существенные нелинейности. Линеаризованные модели, построенные на передаточных функциях, не всегда могут адекватно отобразить электропривод во всех его режимах работы. Но даже при наличии такой модели, в реальных системах применяются более простые программные методы, позволяющие получить грубую идентификацию объекта для автонастройки регулятора и диагностики системы. Это связано с ограниченными ресурсами систем управления по памяти и мощности процессоров.
Искусственные нейронные сети являются альтернативным инструментом идентификации динамических объектов. Существует теорема об универсальной аппроксимации многослойной нейронной сети, утверждающая, что многослойной сети с одним скрытым слоем достаточно для получения равномерной аппроксимации с точностью для любого обучающего множества, представленного входами и желаемых откликов
[1],[3],[4]. В рамках данной статьи рассмотрено применение нейронной сети для частного случая идентификации электропривода постоянного тока. Возможность такого подхода к идентификации ограничивается лишь достаточным количеством обучающих примеров типа «вход-выход» применительно к параметрам конкретного электропривода. Для эксперимента выбрана сеть, известная как модель нелинейной регрессии с внешними входами NARX [2],[4]. Обобщенная модель имеет форму:
где – выходной вектор,
– входной вектор,
– дискретный момент времени,
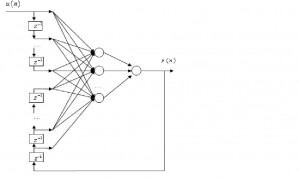
-порядок системы. Такая сеть, имея обратные связи с единичной задержкой, позволяет построить на ее основе модель динамического объекта любой сложности. Ниже приведена структурная схема сети NARX (Рис.1).
Рисунок 1. Рекуррентная многослойная нейронная сеть NARX.
В приложении Simulink среды разработки Matlab было произведено обучение нейронной сети. Обучающее множество снято с модели электропривода постоянного тока при подаче на вход случайного сигнала. Для обучения использовался алгоритм Левенберга-Марквардта. Обучение производилось в течении 300 итераций и ошибка обучения . На 10 секунде подавался момент сопротивления. Результаты моделирования для трех величин
напряжения задания представлены на графике (Рис. 2).
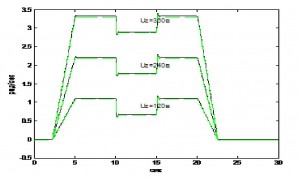
Рисунок 2. График сравнения скоростей модели электропривода и нейросетевой модели.
Из графика видно, что нейронная сеть с достаточной точностью повторяет динамику модели электропривода во всем диапазоне его работы.
Данный метод построения модели не требователен к ресурсам микропроцессорной системы управления, так как не требует решения сложных дифференциальных уравнений. Кроме того, метод может быть применен к электроприводам любой сложности. Недостатком метода является необходимость после обучения модели проверки ее на адекватность новыми данными, не участвовавшими в обучении. Это связано с опасностью переобучения сети [4]. Эта проблема может быть решена программным контролем результата обучения перед применением.
Таким образом, сеть типа NARX можно использовать в составе управляющих алгоритмов в системах управления для идентификации электроприводов, когда имеется возможность получить множество обучающих примеров в рабочем диапазоне. Возможно использование сети NARX при построении полностью нейросетевых систем управления [5] применительно к электроприводам.
Библиографический список
- Горбань А.Н. Обобщенная аппроксимационная теорема и вычислительные возможности нейронных сетей // Сибирский журнал вычислительной математики/РАН. Сибирское отделение. – Новосибирск,1998. –Т.1,№1.-с.11-24
- Макаров И.М., Лохин В.М. Интеллектуальные системы автоматического управления –М. ФИЗМАЛИТ, 2001-576с.
- Терехов В.А. Нейросетевые системы управления / В.А. Терехов, Д.В. Ефимов, И.Ю Тюкин –М.: ИПРЖР,2002. – 480с.
- Хайкин С. Нейронные сети: полный курс, 2-е издание: Пер. с англ. – М.: Издательский дом «Вильямс». 2006. – 1104с.
- Чернодуб А.Н., Дзюба Д.А. Обзор методов нейроуправления – Киев. Институт проблем математических машин и систем НАН Украины.