В настоящее время наиболее актуально провести исследование применения математики и информатики в образовании. Математико-статистические методы применительно к информатике позволят учащимся приобрести опыт логически мыслить, анализировать и исследовать информацию и особый научный опыт.
Приведем примеры применения статистико-математического анализа информационных технологий.
С учетом улучшения технических свойств электронной техники со временем, увеличивается объем обработанной информации за отчетный период.
Sinf = Vinf × tinf
Где Sinf – объем обработанной информации
Vinf – скорость обработки информации
tinf – время обработки информации
Обозначающим индексом 0- отмечаются показатели базисного(прошлого) периода;
Обозначающим индексом 1- отмечаются показатели отчетного(текущего, настоящего) периода.
Абсолютный прирост
объема обработанной информации в текущем периоде, по сравнению с базисным(DSinf ) обусловлен:
1)За счет увеличения скорости обработки информации
= (
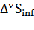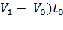– прирост объема информации за отчетный период за счет изменения скорости обработки равен увеличение скорости в текущем периоде по сравнению с прошлым, помноженное на время затраченное на обработку информацию прошлого периода.
2)За счет уменьшения времени затраченного на обработку информации.
= (
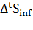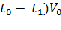– прирост объема информации за отчетный период за счет уменьшения затрат времени на обработку информации равен разности во времени в сторону уменьшения(редко, показатель может быть отрицательным) текущего и базисного периода помноженной на скорость обработки базисного периода.[1,2]
Общий показатель абсолютного изменения времени, затраченного на обработку равен:
DSinf =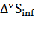 
+ 
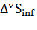
Существуют следующие виды относительных показателей(коэффициентов).[1]
1)Коэффициент динамики (относительные величины динамики)
2)Коэффициент структуры (относительные величины структуры)
3)Относительное линейное отклонение (показатели интенсивности)
4)Коэффициент координации (относительные величины координации)
5)Коэффициент осцилляции (относительные величины сравнения)
Применимо к информатике эти коэффициенты называются так:
1)Относительный показатель динамики обработки информации
ОПДОИ= 
2)Относительный показатель структуры обработанной информации.
ОПСОИ=
Делимое может относиться к финансовой, бухгалтерской и пр.информации.
3)Относительный показатель интенсивности распространения ошибок при прохождении процесса обработки информации.
ОПИРО=
Делимое и делитель в формуле обычно обозначает количество ошибочных прохождений или прерываний программ и общее количество необходимых в работе программ.
4)Относительный показатель координации времени обработки программ.
ОПКВОП=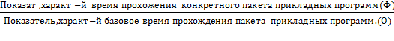 
Ф – фактическое время ;
О – образцовое время.
5)Относительный показатель сравнения обработки информации -коэффициент осцилляции.
ОПСОИ=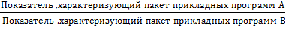
Обычно делимое и делитель формулы означает время обработки ППП, количество программ в ППП и пр.
Если представить нагрузку на различные технические средства обработки информации ,как технику разного порядка совершенства:1,2,3 и т.д.(до 5).
Имеем квадрат 100×100(в %) или если квинтели – 5 × 5 клеток (по 20%).
В квадрате абсцисса(Х)-уровни технических средств обработки от низших к высшим(от 1 до 5).По 20% в каждой градации.
Всю обработанную информацию разделить на квинтили – по 20%
В квадрате Джини 5 квинтильных полосок n=5
Максимально возможное заполнение одной квинтильной полоски
500=(100×100):2
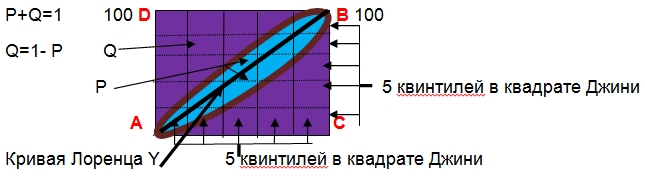
Рисунок 7:
Кривая Лоренца в квинтильном квадрате 5Х5.
P- двойное значения предпоследнего элемента кумуляты Yв % или долях.
P = 2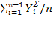 
; Q= 1-P = 1- 2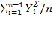 
Коэффициент Джини дифференциации обработки информации на технике разного уровня покажет сколько обработанной (или, чаще необработанной)информации приходится на один квинтиль в среднем. Квинтили учитывают сортировку технических средств от низкого к более высокому уровню.[1]
КДж 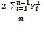=1- 
=1-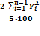 
[500 (5×100),если в %;5 в долях]
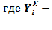сумма накопленного(кумулятивного) значения функции Y(без
последнего значения квинтиля) –в долях или % ,в треугольнике ABC. Так как мы рассматриваем дифференциацию в четырехугольнике ADBC, значение предпоследней кумуляты удваиваем (симметрия).[2]
Значение коэффициента Джини покажет дифференциацию в нагрузке на технику разного уровня.
В образовательной практике информатики важно использовать математико-статистические методы, так как такой симбиоз даст дополнительный опыт знаний предмета.
Библиографический список
-
Статистический словарь; М:,Энциклопедия,2010
-
Статистические методы в экономике. Краткий справочник для специалистов; М:,Энциклопедия,2007.