Предметом данной статьи являются буквенные симметричные квадратные матрицы, точнее говоря буквенные магические квадраты, которые встречаются в комбинаторной литературе и привлекают к себе внимание прежде всего именно как объекты, обладающие свойством симметрии и позволяющие создавать двумерные тексты, укладывающиеся в одном или в комбинации из нескольких таких буквенных магических квадратов с возможностью их различного прочтения. Уже сам по себе алфавит как первоструктура языка наделен магией [4]. Однако, как следует из данной статьи, магические свойства существенно расширяются переносом их, согласно строгим математическим правилам, на сами тексты, т. е. литературные произведения. Комбинаторная словесность располагает широким спектром различных формальных техник написания текстов. Общим для этих техник является тот факт, что рабочим материалом для них служат линейные (одномерные) массивы текста, т.е., в большинстве случаев, строки. В общем же случае линейным (одномерным) массивом текста является вектор-строка или вектор-столбец, состоящие из определенного конечного количества упорядоченных элементов (букв). Нас, конечно же, будут интересовать в первую очередь такие одномерные массивы, которые обладают планом выражения и содержания, т. е. являются словом. Поэтому под словом будем понимать линейный (одномерный) массив текста, т. е. вектор-строку или вектор-столбец, состоящие из конечного количества упорядоченных элементов (букв) и обладающие планом выражения и содержания.
Однако, главной темой данной статьи будут являться не одномерные, а двумерные текстовые массивы (таблицы или, что то же самое, матрицы), которые, в этом смысле, выделяются от стандартных линейных текстов, которыми оперирует комбинаторная словесность, да и словесность вообще, но которые также подпадают под категорию комбинаторных. Двумерный текстовый массив является простейшим видом многомерных массивов и его можно, вообще говоря, представить как одномерный массив, элементами которого, в свою очередь, служат одномерные массивы.
Алгебра матриц
Определим буквенную матрицу размерности m x n как прямоугольную таблицу элементов (букв) 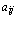 , где i = 1,…m, j = 1,…n, прочитываемых по строкам и столбцам как конечные упорядоченные вектор-строки или вектор-столбцы, обладающие семиотическим планом выражения и содержания, т. е. как значащие слова и которая представляет собой совокупность строк и столбцов, на пересечении которых и расположены эти элементы (буквы). Компактно буквенную матрицу можно обозначить как A = (
, где i = 1,…m, j = 1,…n, прочитываемых по строкам и столбцам как конечные упорядоченные вектор-строки или вектор-столбцы, обладающие семиотическим планом выражения и содержания, т. е. как значащие слова и которая представляет собой совокупность строк и столбцов, на пересечении которых и расположены эти элементы (буквы). Компактно буквенную матрицу можно обозначить как A = (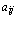 )
)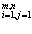 . Здесь первый индекс означает индекс строки i =
. Здесь первый индекс означает индекс строки i = 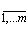 ,
,
а второй – индекс столбца j = 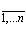 . В развернутом виде будем использовать общепринятую запись вида [1]:
. В развернутом виде будем использовать общепринятую запись вида [1]:
A = 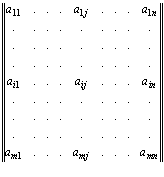
Каждую строку буквенной матрицы мы можем представить себе как вектор-строку в n-мерном пространстве данного алфавита AL , т. е. в подмножестве, состоящем из n букв множества всех букв данного алфавита. Например, i-ю вектор-строку можем записать какAL
, т. е. в подмножестве, состоящем из n букв множества всех букв данного алфавита. Например, i-ю вектор-строку можем записать какAL = ||
= ||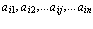 ||. Соответственно каждый столбец буквенной матрицы представляется как вектор-столбец в m-мерном алфавитном пространстве AL
||. Соответственно каждый столбец буквенной матрицы представляется как вектор-столбец в m-мерном алфавитном пространстве AL и j-й столбец записывается в виде:
и j-й столбец записывается в виде:
AL =
= 
Таким образом, вся буквенная матрица может интерпретироваться нами как вектор в алфавитном пространстве AL , имеющем размерность m x n. Это обстоятельство, в частности, позволит нам ниже ввести покомпонентное сложение буквенных матриц.
, имеющем размерность m x n. Это обстоятельство, в частности, позволит нам ниже ввести покомпонентное сложение буквенных матриц.
Если количество строк m буквенной матрицы совпадает с количеством ее столбцов n, т. е. если m = n, то такая матрица называется квадратной. Число m = n называется размером или порядком буквенной матрицы. В противном случае, т. е. в случае, если m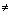 n, буквенная матрица называется прямоугольной.
n, буквенная матрица называется прямоугольной.
Определим еще для квадратной буквенной матрицы понятия главной и побочной диагоналей. Диагональ квадратной буквенной матрицы, проведенная из ее левого верхнего угла в правый нижний угол, т. е. начинающаяся на первом элементе матрицы 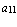 и оканчивающаяся на ее последнем элементе
и оканчивающаяся на ее последнем элементе 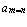 , называется главной диагональю квадратной буквенной матрицы. Элементами главной диагонали являются
, называется главной диагональю квадратной буквенной матрицы. Элементами главной диагонали являются 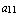 ,
, 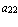 , …
, …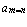 , т. е.
, т. е. 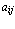 при i = j. Диагональ квадратной буквенной матрицы, проведенная из ее левого нижнего угла в правый верхний угол, т. е., в общем случае, начинающаяся на элементе
при i = j. Диагональ квадратной буквенной матрицы, проведенная из ее левого нижнего угла в правый верхний угол, т. е., в общем случае, начинающаяся на элементе 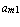 и оканчивающаяся на элементе
и оканчивающаяся на элементе 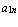 , называется побочной диагональю. Ее элементами являются соответственно
, называется побочной диагональю. Ее элементами являются соответственно 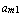 ,
, 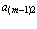 ,…
,… 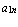 .
.
Введем для буквенных матриц операцию транспонирования. Рассмотрим произвольную абстрактную прямоугольную буквенную матрицу:
A = 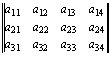
В данном случае m = 3, а n = 4, т. е. данная матрица имеет размерность m x n = 12. Зададимся теперь целью произвести операцию замены всех строк данной буквенной матрицы соответствующими столбцами. Т. е. первую строку поменяем на первый столбец, вторую строку – на второй столбец и т. д. Вот как это будет выглядеть поэтапно:
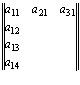
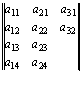
И наконец

Буквенная матрица, получающаяся из исходной заменой строк соответствующими столбцами, называется транспонированной по отношению к исходной матрицей и обозначается A . Т. е. в нашем случае мы получили транспонированную матрицу:
. Т. е. в нашем случае мы получили транспонированную матрицу:
A =
= 
В общем же случае, операция транспонирования связывает с каждой буквенной матрицей A = (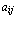 )
)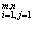 матрицу A
матрицу A = B = (
= B = (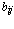 )
)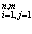 ,
, 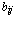 =
=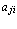 , где i =
, где i = 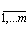 , а j = =
, а j = =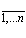 .
.
Рассмотрим теперь не абстрактную, а конкретную буквенную матрицу размерности m x n = 12:
A = 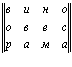
Как видим, здесь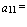 ”в”,
”в”, 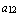 = “и”, …
= “и”, … 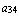 = “а”. В данном случае, читая по строкам, будем иметь текст: “Вино, овес, рама.” Читая, соответственно, по столбцам: “Вор, ива, нем, оса.” Составляя из данной исходной матрицы транспонированную, будем иметь:
= “а”. В данном случае, читая по строкам, будем иметь текст: “Вино, овес, рама.” Читая, соответственно, по столбцам: “Вор, ива, нем, оса.” Составляя из данной исходной матрицы транспонированную, будем иметь:
A =
= 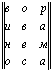
Т. е. получили буквенную матрицу той же размерности, у которой, однако, m = 4, а n = 3. Теперь, читая по строкам, получаем: “Вор, ива, нем, оса.” Читая по столбцам: “Вино, овес, рама.”
Нетрудно убедиться, что исходная буквенная матрица равна своей транспонированной матрице тогда и только тогда, когда исходная буквенная матрица является квадратной и в этом случае еще и симметричной. Говоря о симметрии, мы имеем ввиду симметрию относительно главной диагонали квадратной буквенной матрицы. Это означает, что у такой буквенной матрицы буквы, расположенные симметрично относительно главной диагонали равны. Можно придать этому свойству симметрии более наглядный геометрический смысл. Симметрия буквенной квадратной матрицы означает то, что левый нижний треугольник, образованный первым столбцом, последней строкой и главной диагональю буквенной квадратной матрицы является зеркальным отражением правого верхнего треугольника, образованного первой строкой, последним столбцом и главной диагональю и наоборот. Т. е. при повороте одного из них, скажем, левого нижнего треугольника относительно главной диагонали и наложении его на правый верхний треугольник, соответствующие буквы, образующие эти треугольники совпадут. Можно также сказать, что на прямых, проведенных перпендикулярно главной диагонали, по обе стороны от нее буквы будут располагаться симметрично.
Буквенные магические квадраты
Итак, назовем буквенную симметричную квадратную матрицу A, для которой A =A непалиндромной магической квадратной матрицей или просто непалиндромным магическим квадратом. В таких непалиндромных магических квадратах текст может одинаково прочитываться слева направо по строкам или сверху вниз по столбцам. Всюду, говоря о магических квадратах, мы будем подразумевать буквенные магические квадраты, не оговаривая это особо. Приведем примеры построения непалиндромных магических квадратов. Построим вначале поэтапно непалиндромный магический квадрат порядка m = n = 4:
непалиндромной магической квадратной матрицей или просто непалиндромным магическим квадратом. В таких непалиндромных магических квадратах текст может одинаково прочитываться слева направо по строкам или сверху вниз по столбцам. Всюду, говоря о магических квадратах, мы будем подразумевать буквенные магические квадраты, не оговаривая это особо. Приведем примеры построения непалиндромных магических квадратов. Построим вначале поэтапно непалиндромный магический квадрат порядка m = n = 4:
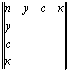
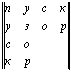


Читая по строкам и столбцам, получаем: “Пуск, узор, сода, краб.” Таким образом, мы изначально построили данную квадратную матрицу так, чтобы она не менялась при транспонировании, т . е. являлась бы симметричной. Видим, что буквы, расположенные симметрично относительно главной диагонали “п з д б” равны, в чем нетрудно убедиться повернув, к примеру, левый нижний треугольник “п у с к р а б д з п” относительно главной диагонали и наложив его на одноименный правый верхний треугольник.
Приведем еще примеры. Вот непалиндромный магический квадрат пятого порядка:
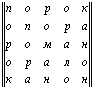
Здесь читаем по строкам и столбцам: “Порок – опора, роман – орало, канон.”
Непалиндромный магический квадрат шестого порядка может выглядеть так:

Читается по строкам и столбцам как: “Логика – огород, города ирония, код и ум, ада яма.”
Будем говорить, что буквенная квадратная матрица является суперсимметричной, если она симметрична как относительно своей главной диагонали, так и относительно побочной диагонали. У такой матрицы буквы, расположенные симметрично главной диагонали равны точно также, как равны между собой соответствующие буквы, расположенные симметрично побочной диагонали. В геометрическом смысле суперсимметрия буквенной квадратной матрицы означает то, что левый нижний треугольник, образованный первым столбцом, последней строкой и главной диагональю буквенной квадратной матрицы является зеркальным отражением правого верхнего треугольника, образованного первой строкой, последним столбцом и главной диагональю и наоборот, в то время как правый нижний треугольник, образованный последней строкой, последним столбцом и побочной диагональю буквенной квадратной матрицы является зеркальным отражением левого верхнего треугольника, образованного первым столбцом, первой строкой и побочной диагональю и наоборот. Т. е. при поворотах относительно главной и побочной диагоналей и наложении друг на друга соответствующих треугольников, буквы, образующие эти треугольники совпадут. Точно также на прямых, проведенных перпендикулярно главной и побочной диагоналям, по обе стороны от них соответствующие буквы будут располагаться симметрично.
Назовем буквенную суперсимметричную квадратную матрицу A, для которой A =A палиндромной магической квадратной матрицей или просто палиндромным магическим квадратом. В палиндромных магических квадратах текст может одинаково прочитываться слева направо (двигаясь сверху вниз) или справа налево (двигаясь снизу вверх) по строкам, а также сверху вниз (двигаясь слева направо) или снизу вверх (двигаясь справа налево) по столбцам. Приведем примеры палиндромных магических квадратов. Рассмотрим вначале палиндромный магический квадрат пятого порядка (m= = n =5):
палиндромной магической квадратной матрицей или просто палиндромным магическим квадратом. В палиндромных магических квадратах текст может одинаково прочитываться слева направо (двигаясь сверху вниз) или справа налево (двигаясь снизу вверх) по строкам, а также сверху вниз (двигаясь слева направо) или снизу вверх (двигаясь справа налево) по столбцам. Приведем примеры палиндромных магических квадратов. Рассмотрим вначале палиндромный магический квадрат пятого порядка (m= = n =5):
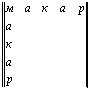
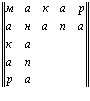
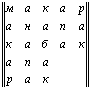
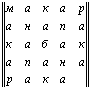

Читая по строкам слева направо, двигаясь сверху вниз или справа налево, двигаясь снизу вверх, получаем: “Макар, Анапа, кабак, а пана ракам!” Читая, соответственно по столбцам сверху вниз, двигаясь слева направо или снизу вверх, двигаясь справа налево, также получаем: “Макар, Анапа, кабак, а пана ракам!” Таким образом, здесь мы имеем дело с суперсимметричной буквенной квадратной матрицей. Видим, что как буквы, расположенные относительно главной диагонали “мнбнм”, так и буквы, расположенные относительно побочной диагонали “рпбпр” равны. Убедиться в этом можно, повернув левый нижний треугольник “макаракамнбнм” относительно главной диагонали и наложив его на одноименный правый верхний треугольник, а также повернув правый нижний треугольник “ракамакарпбпр” относительно побочной диагонали и наложив его на одноименный левый верхний треугольник. На этом примере мы также можем видеть, что в общем случае при нечетном порядке палиндромного магического квадрата, т.е. когдаm = n = 2k + 1, где k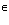 N, т.е. принимает значения чисел натурального ряда, за исключением нуля, срединная строка и срединный столбец (в нашем примере это слово “кабак”), а также сами диагонали (главная и побочная) являются палиндромами, причем если срединные строка и столбец обладают планом выражения и содержания, т. е. являются словом, то обе диагонали, в общем случае, таковым планом не обладают. Первое свойство (т. е. палиндромность срединных строки и столбца) характерно только лишь для палиндромных магических квадратов нечетного порядка. Второе (палиндромность диагоналей) имеет место и в палиндромных магических квадратах четного порядка.
N, т.е. принимает значения чисел натурального ряда, за исключением нуля, срединная строка и срединный столбец (в нашем примере это слово “кабак”), а также сами диагонали (главная и побочная) являются палиндромами, причем если срединные строка и столбец обладают планом выражения и содержания, т. е. являются словом, то обе диагонали, в общем случае, таковым планом не обладают. Первое свойство (т. е. палиндромность срединных строки и столбца) характерно только лишь для палиндромных магических квадратов нечетного порядка. Второе (палиндромность диагоналей) имеет место и в палиндромных магических квадратах четного порядка.
Рассмотрим теперь в качестве примера палиндромный магический квадрат шестого порядка m = n = 6:

Читая по стокам или столбцам в различных направлениях, получаем: “Парт ас, ада ода. Рад мот, том – дар, ад. О, ада сатрап!” Видим, что и здесь обе диагонали являются палиндромами.
В качестве одного из самых ярких примеров буквенных палиндромных магических квадратов можно рассмотреть квадрат SATOR:

Наиболее частый перевод этого палиндромного магического квадрата с латинского выглядит следующим образом: SATOR — сеятель или землепашец, AREPO — выдуманное имя либо производное от ARREPO (в свою очередь от AD REPO - “Я медленно двигаюсь вперед”), TENET — держит, удерживает, OPERA — работы, ROTAS — колеса или плуг. Соответственно сама фраза звучит приблизительно так: “Сеятель Арепо с трудом удерживает колеса” или “Сеятель Арепо управляет плугом (колесами)”. Наиболее мистическим словом в буквосочетании считается слово AREPO, поскольку оно больше не встречается нигде в латинской письменности и считается гапаксом (лингвистический термин, обозначающий слово, встретившееся в некотором текстовом корпусе лишь раз). Часть исследователей полагает, что оно является вымышленным специально для данной композиции. Другие же специалисты придерживаются мнения, что слово было заимствовано из другого языка. Как бы то ни было, этот палиндромный магический квадрат часто ассоциировался с ранними христианами и использовался как талисман либо заклинание. Фраза SATOR OPERA TENET также является примером бустрофедона — способом литературного письма, при котором строки поочередно читаются слева направо и справа налево. Если выражение прочесть дважды в прямом и обратном порядке, то слово TENET повторится.
Уже ранние христиане выяснили, что фраза также является и анаграммой, при перестановке букв которой дважды (с единственной “N”) получается выражение PATER NOSTER, в переводе с латинского означающее “Отче наш” — название одной из основных христианских молитв. Оставшиеся буквы “A” и “O” символизировали “альфу и омегу” — аллегорию, с которой сравнивает себя Господь в Откровении Иоанна Богослова.
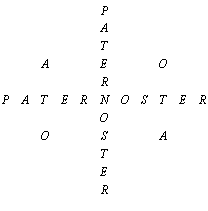
Другая известная фраза, полученная в результате перестановки букв, звучит как PETRO ET REO PATET ROSA SARONA: “Нарцисс Саронский всё ещё раскрыт для Петра, хоть он и виновен”.
Свойства матричных сумм
Поясним сказанное на примере. Пусть имеется прямоугольная абстрактная буквенная матрица размерности m x n = 4 x 3 = 12. Тогда, мы можем, например, прибавить к ней построчно две прямоугольные буквенные матрицы. Одну размерности m x n = 3 x 2 = 6 и другую размерности m x n = 3 x 1 = 3. А постолбцово можно, к примеру, сложить с исходной две буквенные квадратные матрицы порядка m = n = 2. В первом случае получим прямоугольную буквенную матрицу размерности m x n = 7 x 3= = 21:
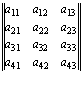 +
+ 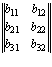 +
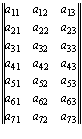
+  =
= 
где 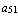 =
= 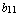 ,
, 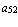 =
= 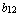 ,
, 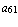 =
= 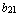 ,
, 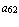 =
= 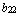 ,
, 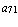 =
= 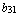 ,
, 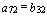 ,
, 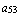 =
= 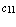 ,
, 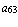 =
= 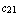 ,
, 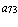 =
= 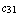 . Во втором – прямоугольную буквенную матрицу размерности m x n = 4 x 5 = = 20:
. Во втором – прямоугольную буквенную матрицу размерности m x n = 4 x 5 = = 20:
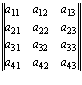 +
+ 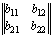 +
+ 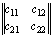 =
=
= 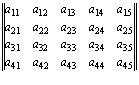
где 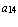 =
= 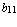 ,
, 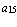 =
= 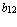 ,
, 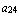 =
= 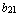 ,
, 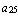 =
= 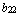 ,
, 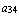 =
= 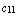 ,
, 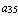 =
= 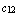 ,
, 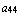 =
= 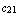 ,
, 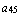 =
= 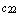 . Естественно, возможны и другие варианты сложения.
. Естественно, возможны и другие варианты сложения.
Нас, конечно же, интересуют прежде всего суммы квадратных буквенных матриц, являющиеся магическими квадратами. В связи с этим зададимся вопросом о том, сколько всего можно создать различных комбинаций сумм из соответствующих чисел складываемых магических квадратов одинакового порядка. Данные суммы назовем комбинаторными, поскольку именно комбинаторика занимается вопросами перестановок и сочетаний элементов, абстрагируясь от природы последних [2]. Будем обозначать отдельные буквенные матрицы как ||1||, ||2|| и т. д.
Пусть даны два магических квадрата (палиндромных или непалиндромных) одинакового порядка. Рассмотрим сколько различных комбинаторных сумм можно из них составить. Эти суммы выглядят следующим образом:
||1|| ||2|| ||2|| ||1||
если складывать буквенные матрицы постолбцово и
||1|| ||2||
||2|| ||1||
если складывать их, соответственно, построчно. Таким образом, всего имеем четыре варианта сумм. Рассмотрим теперь три буквенных магических квадрата. В этом случае имеем:
||1|| ||2|| ||3|| ||1|| ||3|| ||2|| ||2|| ||1|| ||3|| ||2|| ||3|| ||1||
||3|| ||1|| ||2|| ||3|| ||2|| ||1||
если складывать постолбцово и
||1|| ||1|| ||2|| ||2|| ||3|| ||3||
||2|| ||3|| ||1|| ||3|| ||1|| ||2||
||3|| ||2|| ||3|| ||1|| ||2|| ||1||
если складывать построчно. Т. е. здесь уже имеем двенадцать различных видов сумм. Начиная со случая, когда складываются четыре буквенных магических квадрата, последние могут входить в суммы также и в таком виде:
||1|| ||2||
||3|| ||4||
или, скажем
||2|| ||4||
||1|| ||3||
и т. д.
Нетрудно видеть, что в самом общем случае, когда даны N магических квадратов, мы можем составить из них всего M = SN! различных видов комбинаторных сумм, где N! = 1 x 2 x 3 x…x N – факториал (произведение натуральных чисел от 1 до N), а S – число способов представления N в виде произведения двух натуральных чисел, причем в данных произведениях играет роль также порядок расположения множителей, т. е. скажем такие произведения как 1 x 2 и 2 x 1 считаются различными.
Например, в случае выше, когда складывались два магических квадрата мы бы имели: N = 2, N! = 1 x 2 = 2, а S = 2 (это пара 1 x 2 и 2 x 1), тогда M = 2 x 2 = 4, что мы и видели выше. Для N = 3 имеем N! = 1 x 2 x 3 = 6, S = 2 (пара 1 x 3 и 3 x 1) и M = 2 x 6 = 12, что также было видно выше. Для случая N = 4 имеем, соответственно, N! = 1 x 2 x 3 x 4 = 24, S = 3 (это произведения 1 x 4, 4 x 1 и 2 x 2), тогда M = 3 x 24 = 72, т. е. в случае, когда складываются четыре магических квадрата по определенным нами выше правилам, будем иметь всего 72 различных вариантов их сумм. И так далее.
Способы прочтения матричных сумм
Представляет интерес также и вопрос о различных прочтениях комбинаторных матричных сумм, т. е. новых получившихся прямоугольных или квадратных матриц. Несложно заметить, проанализировав эти суммы, что мы также будем иметь P = SN! различных видов их прочтений, что совпадает с количеством видов сумм. В этом случае предполагается, что все складываемые матрицы являются магическими квадратами (палиндромными или непалиндромными) одинакового порядка. Если же все складываемые буквенные квадратные матрицы одного порядка не являются магическими квадратами, то будем иметь всего P = 2SN! всевозможных видов прочтений их сумм. На практике, однако, в большинстве случаев представляет интерес только одно или два каких-либо возможных прочтений двух видов комбинаторных сумм, поскольку именно в этом конкретном случае читаемый текст несет сколько-нибудь существенную смысловую нагрузку.
Рассмотрим, к примеру, два буквенных палиндромных магических квадрата четвертого порядка:
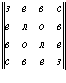 и
и 
Складывая их постолбцово, получим прямоугольную буквенную матрицу размерности m x n = 4 x 8 =32:
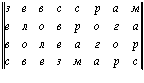
Здесь представляет наибольший интерес постолбцовое прочтение: “Зевс елов воле свез срам, рога, агор Марс.” Или же, читая постолбцово наоборот: “Срам, рога, агор Марс Зевс елов воле свез.” Эти же варианты прочтения можно получить, складывая исходные магические квадраты построчно в прямоугольную буквенную матрицу той же размерности m x n = 8 x 4 = 32:

Читая построчно в прямом и обратном направлениях, получаем такие же варианты прочтения, что и выше. Таким образом, получили два наиболее осмысленных варианта прочтения на примере двух видов сумм двух палиндромных магических квадратов четвертого порядка. Здесь следует отметить, что на первый взгляд нельзя не заметить некоторую неуклюжесть подобного рода текстов, их нарочитую наигранность. К примеру, слово “елов” (сокрашенная форма слова “еловый”) или “агор” (от древнегреческого “агора” – площадь) конечно же не служат украшением никакого литературного произведения. Однако, при более детальном рассмотрении становится ясно, что данная неуклюжесть, которая в среде палиндромистов рассматривается как нечто сопутствующее процессу написанию формальных палиндромных текстов и являющееся его неотъемлемой частью, является своеобразной платой за математическую красоту их структуры.
Рассмотрим еще один пример [3]. Даются четыре палиндромных магических квадрата четвертого порядка:
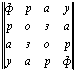



Складывая их постолбцово и построчно, получаем два наиболее осмысленных варианта прочтения их суммы. В первом случае получаем прямоугольную буквенную матрицу размерности m x n = 4 x 16 = 64, а во втором – прямоугольную буквенную матрицу размерности m x n = 16 x 4 = 64:
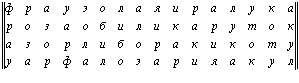
Читая по строкам и столбцам в прямом направлении, получаем: “Фрау Эола! Я – Ира лука. Роза, обил Икар уток. Азор либо раки – коту. У арф алоэ, ария акул.” и “Фрау Роза, Азор у арф Эола обил либо алоэ. Я, Ира, Икар. Раки. Ария. Лука, уток коту акул!” Эти же варианты прочтения имеем, читая по строкам и столбцам в прямом направлении в следующей буквенной матрице:

Здесь также видим, что в тексте присутствует слово “Азор”, столь любимое в среде палиндромистов (примеры палиндромов см. [5]) и обозначающее некое вымышленное имя, однако, как уже было сказано выше, все это не умаляет права подобных текстов на существование.
Заключение
Буквенные матрицы представляют собой наглядный пример двумерных текстовых массивов, а буквенные магические квадраты еще и симметричных массивов текста, являющихся самодостаточными в плане смысловой нагрузки и несущих собственную литературную ценность. Применяя математический метод как инструмент для описания данных симметричных двумерных объектов, мы вскрываем весь глубинный смысл, содержащийся в них, постигая одновременно красоту текстов и гармонию букв. Конечно же, в одной статье невозможно уместить весь спектр проблем и интересных свойств, связанных с буквенными магическими квадратами, однако стоит надеяться, что их исследования продолжатся и в других работах, в различных направлениях, с привлечением возможно нового аналитического аппарата, с целью явить нам всю многогранность этих удивительных объектов.
Библиографический список
- Гантмахер Ф.Р. Теория матриц. М.: Физматлит, 2004.
- Андерсон Джеймс А. Дискретная математика и комбинаторика. М., 2004
- Бонч-Осмоловская Т. Б. Введение в литературу формальных ограничений. Самара: Бахрах- М, 2009
- Пенник Н. Магические алфавиты. М.: София, 1996
- Федин С.Н., Лукомников Г.Г. Антология русского палиндрома, комбинаторной и рукописной поэзии. М.: Гелиос-АРВ, 2002.

 , имеющем размерность m x n. Это позволяет нам ввести покомпонентное сложение буквенных матриц по определенному нами закону. Будем считать, что одна буквенная матрица может прибавляться к другой построчно или постолбцово, т. е. путем добавления строк и столбцов. Это означает, что количество столбцов исходной буквенной матрицы должно совпадать с количеством столбцов каждой из прибавляемых к исходной буквенных матриц или же равняться их сумме, если сложение буквенных матриц происходит построчно. Если же буквенные матрицы складываются постолбцово, то уже количество строк исходной буквенной матрицы должно совпадать с количеством строк каждой из прибавляемых к исходной буквенных матриц или же равняться их сумме.
, имеющем размерность m x n. Это позволяет нам ввести покомпонентное сложение буквенных матриц по определенному нами закону. Будем считать, что одна буквенная матрица может прибавляться к другой построчно или постолбцово, т. е. путем добавления строк и столбцов. Это означает, что количество столбцов исходной буквенной матрицы должно совпадать с количеством столбцов каждой из прибавляемых к исходной буквенных матриц или же равняться их сумме, если сложение буквенных матриц происходит построчно. Если же буквенные матрицы складываются постолбцово, то уже количество строк исходной буквенной матрицы должно совпадать с количеством строк каждой из прибавляемых к исходной буквенных матриц или же равняться их сумме.