1. Введение

В различных областях научно-исследовательской и производственной деятельности человека встречается задача обработки экспериментальных данных с целью извлечения из них закономерностей, описывающих различные процессы и явления. Если изучающиеся закономерности представляются в виде математических моделей, они носят название моделей идентификации, а задача их восстановления – задачи идентификации.

Построение математических моделей разбивается на две подзадачи – структурную идентификацию (определение конкретной формы, структуры модели) и параметрическую идентификацию (определение параметров модели при уже известной её структуре). Остановимся на задаче параметрической идентификации.

2. Анализ существующих решений

Существующие алгоритмы параметрической идентификации обладают рядом существенных недостатков. Во-первых, результат работы большинства алгоритмов сильно зависит от качества начального приближения решения. Во-вторых, для работы алгоритмов требуется наличие обеих производных на всем интервале поиска. Стоит так же отметить, что даже при наличии производных во многих случаях вычисление их остается крайне трудоемким. В-третьих, алгоритмы плохо работают с многоэкстремальными функциями. Так же одним из недостатков можно назвать невозможность к распараллеливанию большинства алгоритмов, что не позволяет никак сократить время их работы.

В качестве решения данных проблем предлагается представить задачу параметрической идентификации в виде задачи многоэкстремальной оптимизации. Минимизируемой функцией в данном случае будет сумма квадратов отклонений расчетных значений от экспериментальных данных.

В качестве алгоритма многоэкстремальной оптимизации был выбран индексный метод. Индексный метод по сравнению с другими методами обладает рядом преимуществ. К ним можно отнести в первую очередь детерминированность алгоритма, возможность к распараллеливанию и то, что индексный метод является методом глобального поиска, что позволяет его без ограничений применять для многоэкстремальных задач.

3. Индексный метод глобальной оптимизации

Алгоритмы, многоэкстремальной оптимизации, предполагают следующую постановку задачи

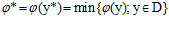
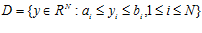
где целевая функция 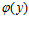удовлетворяет условию Липшица с соответствующей константой L , а именно

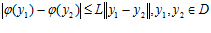
Используя кривые типа развертки Пеано y(x), однозначно отображающие отрезок [0 , 1] на N -мерный гиперкуб P

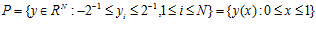
исходную задачу можно редуцировать к следующей одномерной задаче:

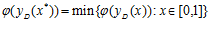
Рассматриваемая схема редукции размерности сопоставляет многомерной задаче с липшицевой минимизируемой функцией одномерную задачу, в которой целевая функция удовлетворяет равномерному условию Гельдера [4], т.е.

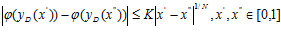
где N есть размерность исходной многомерной задачи, а коэффициент K связан с константой Липшица L исходной задачи соотношением .

Различные варианты индексного алгоритма для решения одномерных задач и соответствующая теория сходимости представлены в работах [1], [3].

4. Редукция размерности и множественные отображения

Редукция многомерных задач к одномерным с помощью разверток имеет такие важные свойства, как непрерывность и сохранение равномерной ограниченности разностей функций при ограниченности вариации аргумента. Однако при этом происходит потеря части информации о близости точек в многомерном пространстве, так как точка x ∈
[0,1] имеет лишь левых и правых соседей, а соответствующая ей точка 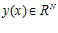имеет соседей по 2^N

направлениям. А при использовании отображений типа кривой Пеано близким в N – мерном пространстве образам y’, y” могут соответствовать достаточно далекие прообразы x’, x” на отрезке [0,1]. Как результат, единственной точке глобального минимума в многомерной задаче соответствует несколько (не более 2^N) локальных экстремумов в одномерной задаче, что, естественно, ухудшает свойства одномерной задачи.

Сохранить часть информации о близости точек позволяет использование множества отображений

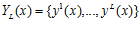
вместо применения единственной кривой Пеано y (x) (см. рис. 1). Каждая кривая Пеано yⁱ(x) из Y_L(x) может быть получена в результате поворота развертки вокруг начала координат. При этом найдется отображение yⁱ(x), которое точкам многомерного пространства y’, y”, которым при исходном отображении соответствовали достаточно далекие прообразы на отрезке [0,1], будет сопоставлять более близкие прообразы x’, x”.

Максимальное число различных поворотов развертки, отображающей N-мерный гиперкуб на одномерный отрезок, составляет 2^N. Использование всех из них является избыточным. В используемой схеме преобразование развертки осуществляется в виде поворота на угол ±π/2 в каждой из координатных плоскостей. Число подобных пар поворотов определяется числом координатных плоскостей пространства, которое равно 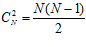, а общее число преобразований будет равно N(N−1). Учитывая исходное отображение, приходим к заключению, что данный способ позволяет строить до N(N−1)+1 развертки для отображения N-мерной области на соответствующие одномерные отрезки.

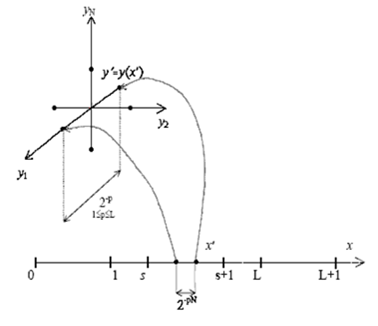
Рис. 1 Множественное отображение

5. Параллельная реализация индексного метода

Использование множества отображений

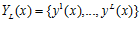
приводит к формированию соответствующего множества одномерных многоэкстремальных задач

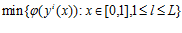
Каждая задача из данного набора может решаться независимо, при этом любое вычисленное значение 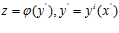функции φ(y) в i-й задаче может интерпретироваться как вычисление значения 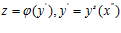для любой другой s-й задачи без повторных трудоемких вычислений функции φ(y). Подобное информационное единство позволяет решать исходную задачу путем параллельного решения индексным методом L задач на наборе отрезков [0,1]. Каждая одномерная задача решается на отдельном процессоре. Для организации взаимодействия на каждом процессоре создается L очередей, в которые процессоры помещают информацию о выполненных итерациях.

При параллельной реализации индексного метода решающие правила алгоритма в целом совпадают с правилами последовательного алгоритма, кроме способа проведения испытания:

•    После выбора точки очередной итерации поиска процессор информирует о произведенном выборе все остальные процессоры;

•  Каждый процессор после проведения испытания в точке итерации передает полученный индекс и значение функции всем процессорам вычислительной системы;

•    Перед началом очередной итерации каждый процессор использует все полученные данные для расширения имеющегося набора с поисковой информацией

6. Результаты вычислений

Были проведены численные эксперименты для определения ускорения параллельной версии алгоритма на процессоре Intel Core i7 с числом потоков от 1 до 8.

Структура модели была задана в виде:

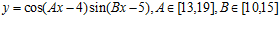
Была задана следующая таблица экспериментальных значений

Таблица 1 – Экспериментальные значения

В результате работы алгоритма были получены следующие значения параметров: A= 15.974; B = 11.985. Вид найденной нелинейной модели представлен на рисунке 2.

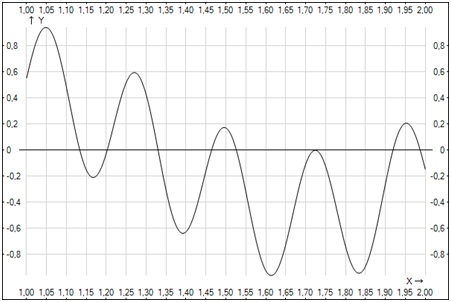
Рис. 2. Вид найденной нелинейной модели

В таблице 2 представлены результаты численных экспериментов работы параллельной версии алгоритма с различным количеством потоков.

Таблица 2 – Результаты численных экспериментов

Полученные результаты позволяют говорить о том, что предложенный алгоритм параметрической идентификации нелинейных моделей чрезвычайно эффективен (особенно его параллельная реализация) и может быть использован для широкого класса моделей. Преимуществами разработанного алгоритма являются детерминированность, высокая степень параллельности, возможность использования функциональных ограничений для каждого параметра модели.

Список литературы

1.    Стронгин Р.Г. Численные методы в многоэкстремальных задачах. (Информационно-статистические алгоритмы). М.: Наука, 1978.

2.    Баркалов К.А. Ускорение сходимости в задачах условной глобальной оптимизации. Нижний Новгород: Изд-во Нижегородского гос. ун-та, 2005.

3.    Strongin R.G., Sergeyev Ya.D. Global optimization with non-convex constraints. Sequential and parallel algorithms. Kluwer Academic Publishers, Dordrecht, 2000.

---

Количество просмотров публикации: Please wait

Все статьи автора «Бородина Екатерина»