Объем информации во всемирной паутине постоянно увеличивается. В связи с этим пользователи сталкиваются со сложной задачей поиска информации, которая бы соответствовала их предпочтениям. Для ее решения, все более важным становится разработка информационных систем, позволяющих автоматизировать процесс рекомендации объектов потребления. Создание качественной рекомендательной системы, с одной стороны, может привести к увеличению прибыли поставщиков услуг (товаров), а с другой − экономии времени потребителя на поиски необходимой вещи. Таким образом, подобные системы очень важны как для экономики, так и для информационного общества в целом.
При создании рекомендательных систем чаще всего используют методы коллаборативной фильтрации [1]. Эти методы определяют возможные предпочтения пользователя, основываясь на известных предпочтениях других пользователей. В их основе лежит идея, что если пользователи A и Б оценили несколько объектов приблизительно одинаково, то и последующие объекты они будут оценивать так же.
Примерами успешных рекомендательных систем, которые основаны на коллаборативной фильтрации, являются системы компаний Amazon и Netflix. Однако, несмотря на активные научные исследования в области коллаборативной фильтрации с 1994 года и успешное использование коллаборативной фильтрации в системах электронной коммерции и цифровой дистрибуции, эта область продолжает оставаться сферой научных интересов. Это связано с рядом проблем, для которых не было найдено удовлетворительных решений [1]. Одной из таких проблем является проблема масштабирования систем коллаборативной фильтрации, которая тесно связана с проблемами анализа данных большой размерности. При анализе данных большой размерности возникает ряд трудностей, получивших название «проклятие размерности».
Эффективными методами для решения задач коллаборативной фильтрации данных большой размерности являются методы поиска приближенных ближайших соседей [2],[3] и методы кластерного анализа [5]. Применительно к коллаборативной фильтрации исследователями предлагалось использовать эти методы по отдельности. Однако нахождение приближенных ближайших соседей позволяет существенно ускорить процесс кластеризации.
Метод коллаборативной фильтрации LSHClust
На основе идеи использования приближенных ближайших соседей для ускорения кластеризации был разработан метод коллаборативной фильтрации LSHClust, который состоит из двух этапов: создание модели (выполняется в фоновом режиме) и формирование списка рекомендаций или прогнозирование оценок (выполняется в режиме реального времени).
Этап создания модели состоит из следующих шагов:
-
Выбор параметров для алгоритма кластеризации.
-
Кластеризация пользователей коллаборативной системы с помощью алгоритма кластеризации LSH-CLC, который разработан для реализации нового метода.
-
Создание модели, которая представляет собой s векторов {c1 , c2 , … , cs}, каждый из которых имеет длину m и является центроидом соответствующего кластера.
Формирования списка рекомендаций осуществляется для активного пользователя, который характеризуется вектором предпочтения (r1, r2,…,rm), гдe ri — оценка, поставленная i-му объекту. Для того чтобы сформировать список рекомендаций необходимо выполнить следующие шаги:
-
Вычислить коэффициент сходства между вектором предпочтения активного пользователя и центроидами s кластеров. В качестве коэффициента сходства может использоваться коэффициент корреляции Пирсона.
-
Выбрать центроиды, для которых коэффициент сходства превышает порог d.
-
Вычислить прогнозируемые значения оценок с помощью формулы:
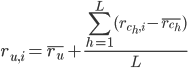
, где 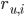 – прогнозируемая оценка, которую пользователь u поставит объекту i;
– прогнозируемая оценка, которую пользователь u поставит объекту i; 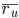 – средняя оценка пользователя u;
– средняя оценка пользователя u; 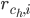 -
-
оценка, которую кластер 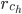 “поставил” объекту i;
“поставил” объекту i;
L - количество кластеров, для которых коэффициент сходства превышает порог d.
-
Формирование списка рекомендаций путем отбора объектов, для которых прогнозируемые оценки максимальны.
Шаги этапа создания модели похожи на шаги метода ClustKNN [6]. Существенным отличием разработанного метода является использование иерархической кластеризации вместо плоской кластеризации.
Алгоритм иерархической кластеризации LSH-CLC
Основой метода LSHClust является алгоритм кластеризации пользователей LSH-CLC. Данный алгоритм основан на методе локально-чувствительного хеширования [7], который решает задачу поиска приближенных ближайших соседей. На основе найденных ближайших соседей (схожих пользователей) впоследствии формируются кластеры (группы по интересам).
Шаги алгоритма LSH-CLC:
-
Для каждого пользователя u
вычислить l сигнатур g1(Iu), g2(Iu), …, gl(Iu), где Iu – множество объектов, которые оценил пользователь. Затем добавить пользователя u в хеш-таблицу Hi так, чтобы сигнатура gi(Iu) была ключом. Таким образом, ячейка хеш-таблицы с ключом gi(Iu) будет представлять собой множество пользователей (приближенных ближенных ближайших соседей). В качестве семейства локально-чувствительных функций используется семейство, образуемое методом MinHash [8].
-
Найти кластеры, которые удовлетворяют следующим условиям:
-
кластеры содержат пользователей, для которых совпадают сигнатуры по крайней мере в одной хеш-таблице;
-
размер обоих кластеров не превышает N;
-
сходство между центроидами кластеров не меньше t.
-
-
Объединить кластеры, найденные на шаге 2.
-
Если есть кластеры, разрешенные для объединения, и t > tmin, уменьшить t и перейти на шаг 2. Иначе прервать работу алгоритма.
Рассмотрим параметры алгоритма LSH-CLC.
-
Количество хеш-функций для вычисления сигнатур k определяет точность нахождения приближенных ближайших соседей. Чем больше это значение, тем больше вероятность того, что именно для ближайших соседей совпадут сигнатуры. Но если это значение будет достаточно велико, то вероятность совпадения сигнатур для двух пользователей будет мала. Выбор значения параметра k определяется эмпирическим путем.
-
Начальное значение порога коэффициента сходства t определяет насколько близки должны быть два кластера, чтобы они были объединены на первой итерации. При использовании меры сходства, которая принимает значения от 0 до 1, значение параметра t должно быть близко к 1. Очевидно, что значение очень близкое к 1 может привести к тому, что на первых итерациях кластеры не будут объединяться.
-
Множитель для порога коэффициента сходства A определяет во сколько раз будет уменьшено значение t` при переходе на следующую итерацию. Большое значение A приводит к уменьшению количества итераций и соответственно уменьшению времени исполнения. Маленькое значение A приводит к более точной кластеризации, но при этом увеличивается время исполнения.
-
Минимальный порог коэффициента сходства tmin ограничивает количество итераций. Маленькое значение этого параметра может привести к ухудшению качества кластеризации, поскольку в этом случае могут объединяться не очень схожие кластеры. Большое значение tmin может привести к тому, что кластеры будут содержать очень маленькое количество пользователей.
-
Количество хеш-таблиц l
определяет сколько сигнатур будет вычисляться от векторов предпочтений пользователей. При большом количестве пользователей желательно установить это значение достаточно большим для увеличения количества множеств приближенных ближайших соседей.
-
Максимальный размер кластера N введен для ограничения количества пользователей в кластере для того, чтобы сократить время исполнения алгоритма.
Сложность алгоритма LSH-CLC составляет O(nB), где n – количество пользователей, а B – максимальное количество пользователей, для которых совпала сигнатура при генерации хеш-таблиц.
Результаты экспериментальных исследований
Для проведения экспериментов использовался популярный набор данных, который был собран в результате работы проекта MovieLens и был опубликован исследовательской лабораторией GroupLens Research. Набор данных MovieLens содержит оценки различным фильмам. Он включает 6040 пользователей, 3900 фильмов и 1000209 оценок.
Для экспериментов история оценок каждого пользователя была разделена на два непересекающихся множества: обучающее и тестовое. Тестовое множество было сформировано путем отбора 20% случайных оценок из всего множества оценок пользователя. Таким образом, обучающее множество включало 80% оценок от начальных данных. Используя обучающее множество, создавалась модель коллаборативной фильтрации. После создания модели, она оценивалась с помощью тестового множества.
На рисунке 1 показана зависимость качества прогнозирования от параметра tmin. Точность прогнозирование оценивается с помощью среднего абсолютного отклонения значений тестовых оценок от прогнозируемых оценок. Чем меньше значение MAE, тем лучше.
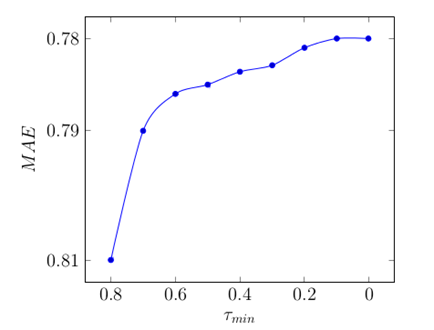
Рис. 1 – Зависимость средней абсолютной ошибки от значения минимального для объединения кластеров
Как видно по графику, минимальное значение ошибки равно 0.78.
Для сравнения, метод основанный на сингулярном разложении матриц (SVD), на том же наборе данных показал точность 0.77. А метод RecTree — 0.82 [9].
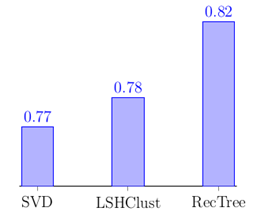
Рис. 2 – Точность прогнозирования метода LSHClust в сравнении с методом RecTree и методом, основанном на SVD
Для оценки времени исполнения алгоритмов, которые реализуют метод, было создано несколько наборов данных (размером от 1000 до 6000 пользователей). На рисунке 3 показана зависимость времени формирования списка рекомендаций для всех пользователей соответствующего набора. Графики приведены для метода LSHClust и для метода, основанного на алгоритме kNN (K-nearest neighbor). В алгоритме kNN осуществляется поиск K-пользователей с наиболее похожими оценками путем сравнения вектора предпочтений пользователя с векторами предпочтений всех других пользователей. Очевидно, что сложность kNN составляет O(n2).
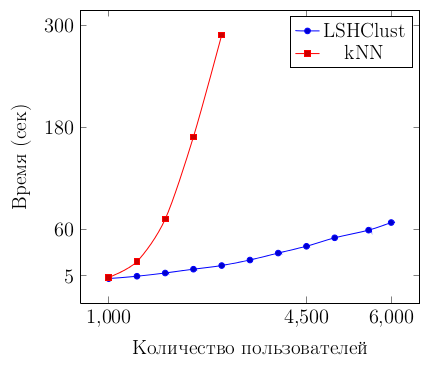
Рис. 3 – Зависимость времени выполнения алгоритмов для создания модели и формирования списка рекомендаций от количества пользователей в системе
Как видно из последнего графика, время выполнения алгоритма с ростом количества пользователей растет линейно.
Заключение.
В статье был представлен метод коллаборативной фильтрации LSHClust, который достаточно прост для реализации, обладает хорошими показателями масштабируемости. При этом разработанный метод позволяет достичь точности прогнозирования оценок, сравнимой с одним из самых точных методов (основанным на SVD). Большое количество параметров позволяет гибко настроить метод под различные рекомендательные системы.
Библиографический список
- Su, Xiaoyuan, and Taghi M Khoshgoftaar. <<A survey of collaborative filtering techniques.>> Adv in Artif Intell 2009 (2009) : 2. Print.
- Bachrach, Yoram, Ely Porat, and Jeffrey S Rosenschein. “Sketching Techniques for Collaborative Filtering.” International Joint Conference on Artificial Intelligence (2009) : 2016-2021.
- Das, A S et al. “Google news personalization: scalable online collaborative filtering.” Proceedings of the 16th international conference on World Wide Web. ACM, 2007. 271-280.
- Han, S et al. “RecTree : An Efficient Collaborative Filtering Method.” Matrix (2001) : 141–151.
- Ungar, Lyle H, and Dean P Foster. “Clustering Methods for Collaborative Filtering.” AAAI Workshop on Recommendation Systems pp.1 (1998) : 1-16.
- Al, Mamunur Rashid et al. “ClustKNN: a highly scalable hybrid model- memory-based CF algorithm.” KDD Workshop on Web Mining and Web Usage Analysis. ACM, 2006.
- http://en.wikipedia.org/wiki/Locality-sensitive_hashing
- http://en.wikipedia.org/wiki/MinHash
- Han, S et al. “RecTree : An Efficient Collaborative Filtering Method.” Matrix (2001) : 141–151.
