Задача распределения военных ресурсов предназначена для получения рекомендаций лицам при принятии решений по своевременному обеспечению ресурсами формирований.
На основе данных об обеспеченности ресурсами формирований строится модель их распределения.
Количество j-ого ресурса Vj, подаваемого из довольствующего органа l-ому формированию, определяется как разность нормы j-ого ресурса Nj для l-ого формирования и обеспеченность j-ым ресурсом Sj:
Vj = Nj – Sj
.
Общее количество ресурсов V, которые необходимо передать всем формированиям определяется как:
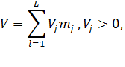
где Vj – количество j-ого ресурса, подаваемого из довольствующего органа l-ому формированию;
mj – масса j-ого ресурса;
L– количество формирований.
Количество подач ресурсов определяется по формуле:
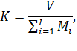
где V – общее количество ресурсов;
Mi – грузоподъемность транспорта;
I – количество транспорта в довольствующем органе.
Каждый ресурс имеет определенную ценность, т.е. больший приоритет одного вида ресурса перед другим.
Для каждой подачи K определим математическую постановку задачи:
Пусть задано конечное множество различных видов ресурсов 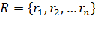 , для каждого
, для каждого 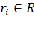
известна ценность ci и определена масса mi.
Имеется транспорт грузоподъемностью M. Требуется загрузить транспорт так, чтобы общая ценность упакованных ресурсов была наибольшей и их масса не превосходила M.
Введем двоичные переменные x1, x2, … xn:
-
x = 1, если ресурс
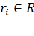 выбран для погрузки;
выбран для погрузки;
-
xi= 0 в противном случае.
Необходимо найти такие значения переменных, при которых достигается максимум суммы
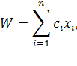
и выполняется ограничение
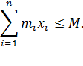
Данная задача представляет собой задачу об одномерной оптимальной упаковке. Для ее решения построим модель динамического программирования и решим задачу табличным методом.
Идея постепенной, пошаговой оптимизации лежит в основе табличной реализации метода динамического программирования. Принцип динамического программирования не предполагает, что каждый шаг оптимизируется отдельно, независимо от других. Шаговое управление должно выбираться дальновидно, с учетом всех его последствий в будущем.
Общий принцип, лежащий в основе решения задач динамического программирования: каково бы ни было состояние процесса перед очередным шагом, надо выбирать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным. Это более конкретная перефразировка принципа оптимальности Беллмана.
Однако из этого принципа есть исключение. Среди всех шагов есть один, который можно планировать без оглядки на будущее. Это последний шаг.
Поэтому процедура решения задачи динамического программирования обычно разворачивается от конца к началу. Вначале планируется последний n-ый шаг. При этом делаются разные предположения о том, чем закончился предпоследний (n − 1)-шаг. Для каждого из этих предположений следует найти условное оптимальное управление на n-ый шаг. «Условное» потому, что оно выбирается исходя из условия, что предпоследний шаг закончился так-то и так-то. Далее, «пятясь назад» оптимизируется управление на (n − 1)-м шаге и т.д., пока не будет достигнут первый шаг.
Предположим, что все условные оптимальные управления и условные оптимальные выигрыши найдены для всего «хвоста» процесса. Далее выполняется построение не условно оптимального, а просто оптимального управления
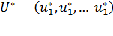 и вычисление не условно оптимального, а просто оптимального выигрыша Wmax.
и вычисление не условно оптимального, а просто оптимального выигрыша Wmax.
Таким образом, при построении оптимального решения многошаговый процесс «проходится» дважды:
-
сначала – от конца к началу, в результате чего находятся условные оптимальные управления и условные оптимальные выигрыши на оставшийся «хвост» процесса;
-
после – от начала к концу, когда выписываются уже готовые рекомендации и находится оптимальное управление.
Для следующей итерации, т.е. загрузки следующего транспортного средства, аналогично строится модель динамического программирования с учетом укомплектованности транспорта на предыдущем шаге. Процесс продолжается пока количество подач не достигнет K.
Представленная математическая модель относится к типу оперативных моделей, используемых в подсистеме управления базой моделей системы поддержки принятия решений.
Библиографический список
