Велиховский О.В., инженер, бакалавр кафедры

электрические системы и сети, КПИ, г. Киев

Исходные данные

Предположим, что задано некоторое конечное множество вершин в трёхмерном Евклидовом пространстве и множество неупорядоченных пар из этих вершин

|E |= n , |V |= m , ( n,m ) =1,2,3,… (1)

Таким образом задан неориентированный симметричный граф:

G ( V , E )

На заданном графе требуется построить минимальный элементарный цикл или цикл Гамильтона.

Метод построения

Для решения задачи построения будем применять некоторый предикат :

R ( V , E )

Такой предикат будем называть предикатом выбора по наиболее удалённой паре вершин или по диаметру графа

R ( V, E ) = R ( diam(G) ) (2)

В связи с их простотой совместим первый и второй этапы построения. Для этого выберем ребро максимальной величины по наибольшему расстоянию между парами заданных вершин

(v₁ ,v₂) T | V | (3)

E_max=E_n=diam(G) (4)

Затем выберем следующую вершину v₃
из | V | , которая находится на максимальном расстоянии от одной из вершин диаметра или одного из полюсов
Вершины образующие диаметр графа будем называть полюсами графа и обозначать (V ,U )

E_n = {V, U }
(5)

Каждую последующую по очереди вершину или новую верщину будем так же определять, как вершину которая наиболее удалена от одной из пары вершин образующих диаметр графа diam(G) и которая будет определять следующее по порядку наибольшее ребро графа последовательно меньшее диаметра графа .

Соединим вершины ребра Е_n= diam(G) c вершиной v₃ по кратчайшему пути, то есть минимальному расстоянию между ними , соответственно.

Для наглядного представления предположим , что множество всех вершин | V |
расположено внутри некоторой мнимой сферы, и такая сфера сжимается равномерно по всем направлениям. Тогда поверхность этой сферы будет последовательно касаться всех вершин, начиная от самых удалённых друг от друга и заканчивая менее удалёнными соответственно, до тех пор пока поверхность этой сферы коснётся (соединит) всех вершин |V| в порядке уменьшения расстояния между ними .

Далее выберем следующую новую вершину v₄ , которая будет так же максимально удалена от одного из полюсов графа. Соединим вершину v₄ с вершинами ближайшего к ней ребра из предыдущего цикла, одна из вершин такого ближайшего ребра будет находиться на минимальном расстоянии от новой вершины v₄ , а другая вершина такого ребра будет находиться на максимальном расстоянии от вершины или полюса диаметра графа, которая является ближайшей к новой вершине v₄ .

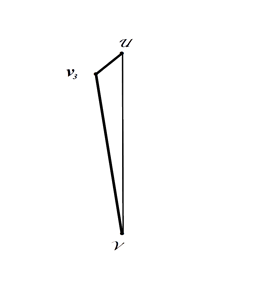
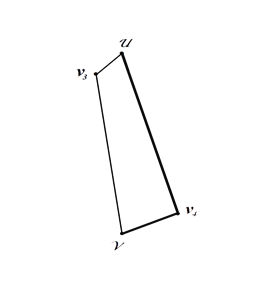
Рисунок 1.                                                    Рисунок 2.

Из рисунка 2 видно, что на первом и втором этапах построения из цикла исключается ребро E_n= diam(G). В результате был построен цикл Гамильтона, состоящий из четырёх вершин .

На следующих двух этапах определяем новую вершину v₅ следующую за вершиной v₄ по максимальной удалённости от одного из полюсов графа и новую вершину v₆ следующую за вершиной v₅ по максимальной удалённости от одного из полюсов графа. Затем соединяем новые вершины аналогично предыдущему этапу построения с ближайшими к ним рёбрами соответственно. Сначала с ближайшей вершиной из предыдущего цикла, а затем с вершиной того же ребра максимально удалённой от полюса графа ближайшего к новой вершине соответственно .

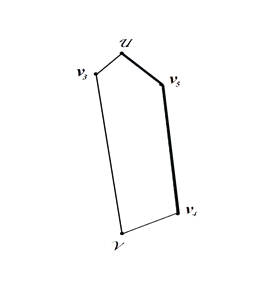
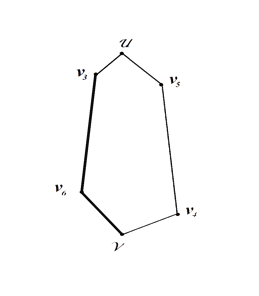
Рисунок 3.                                               Рисунок 4.

Из рисунка 4 видно, что на втором и третьем этапах построения из цикла исключаются ребра ближайшие к новым вершинам v₅ и v₆ . В результате был построен цикл Гамильтона состоящий из шести вершин .

На следующих этапах построения проводятся аналогично предыдущим этапам для любого количества новых вершин v_m из | V | . В результате будет построен цикл Гамильтона для всех заданных вершин | V | и по величине состоящий из множества рёбер | E_k | .

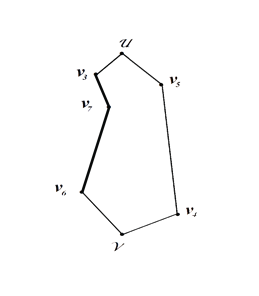
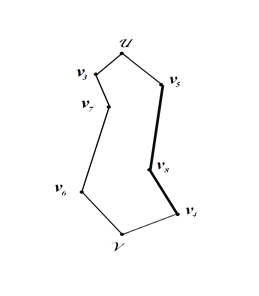
 Рисунок 5.                                                                                  Рисунок 6.

На рисунке 6 построен цикл Гамильтона состоящий из восьми вершин .

Для построения минимального цикла Гамильтона входные данные должны определять все минимальные значения расстояний между заданными вершинами и все значения расстояний между вершинами и полюсами графа.

Таким же методом можно построить все последующие циклы, начиная от минимального цикла Гамильтона и далее следующие с увеличением по величине друг за другом. Для этого на каждом новом этапе построения необходимо каждую новую вершину соединять с вершиной из предыдущего цикла следующей по величине за ближайшей по отношению к новой вершине, то есть с ребром из предыдущего цикла следующего сразу за ближайшим к новой вершине ребром из предыдущего цикла.

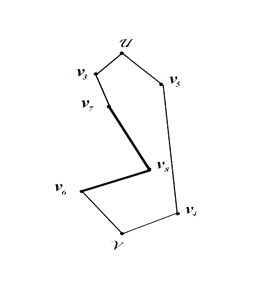
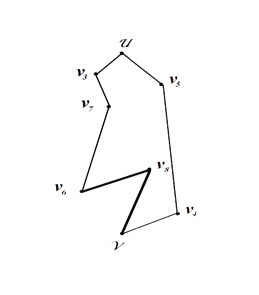
Рисунок 7.                                                                  Рисунок 8.

На рисунках 7 и 8 построены два очередных элементарных цикла, следующих сразу за минимальным циклом Гамильтона по увеличению | E |

| E_k |< | E_k-1|< | E_k-2| (6)

Построение максимального цикла Гамильтона

Аналогичным методом можно построить так же и максимальный цикл Гамильтона. Для этого выбираем каждую новую вершину, как максимально удалённую от одного из полюсов графа, аналогично предыдущему методу. Далее необходимо каждую новую вершину соединять с наиболее удалённым от неё ребром. Одна из вершин такого, максимально удалённого ребра будет находиться на максимальном расстоянии от очередной новой вершины, а вторая вершина того же ребра будет ближайшей к полюсу графа максимально удалённого от очередной новой вершины.

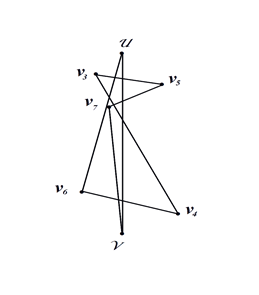
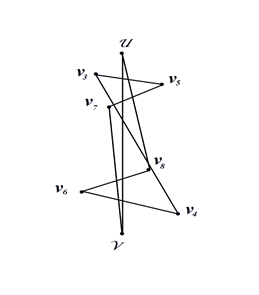
Рисунок 9.                                                                             Рисунок 10.

На рисунке10 изображён цикл Гамильтона максимальной величины, состоящий из восьми вершин .

Упрощение построений

Построение элементарного цикла можно упростить, если вместо диаметра графа использовать параметр радиуса графа radius(G). Тогда вместо расстояний между вершинами и полюсами графа в построении будут принимать участие расстояния от вершин до мнимого центра диаметра графа и минимальные расстояния между вершинами графа | V |.

Количество шагов для построения описанного элементарного цикла равняется количеству заданных вершин, уменьшенное на две единицы

| R( V, E )| = (| V_m| - 2) (8)

(|V|,|E |) >2 (9)

Таким образом задача построения минимального цикла Гамильтона разрешима при помощи предиката выбора R(V,
E) за полиномиальное время и принадлежит классу P.

Дополнение

Допустим, что будут справедливы следующие соответствия между представлениями множества слов  x  из языка L на алфавите 


V = 


E  =  x (11)

G (V ,E ) = L (12)

Предикат выбора R( V, E ) обозначим как D – (define), а задачу построения некоторого элементарного цикла как C  (cycle), тогда будем говорить, что некоторое высказывание C из языка L на алфавите  разрешимо при помощи предиката выбора D ( V ,E ) за полиномиальное время 

C ( V, E ) T P (13)

Свойство селективности цикла Гамильтона определяет существование диаметра графа diam(G), по которому определён предикат выбора R(V, E).

Если существует некоторый предикат выбора D для языка L на алфавите  , тогда некоторое высказывание C из языка L разрешимо алгоритмически в классе P.

Список литературы:

1. Гэри М., Джонсон Д. Вычислительные машины и трудно решаемые задачи., М.: Мир, 1982.
   
2. Лорьер Ж.-Л. Системы искусственного интеллекта., М.: Мир, 1991.

Все статьи автора «Oleg Velikh»