К ВОПРОСУ О НЕОПРЕДЕЛЕННОСТИ, СЛУЧАЙНОСТИ И НЕЧЕТКОСТИ В СОЦИАЛЬНО – ЭКОНОМИЧЕСКИХ ЗАДАЧАХ КЛАССИФИКАЦИИ

Первый этап становления любой области знания как науки неизбежно начинается с решения проблемы систематизации объектов ее изучения. Процесс систематизации (классификации) объектов имеет огромное практическое значение, суть которого точно описал Ю.П. Адлер [1]: «Данные наступают на нас со всех сторон. Они накапливаются в темпе, значительно опережающем нашу способность их ассимилировать и использовать. Мы их «складируем впрок», порождая огромные архивы и сложнейшие проблемы хранения, переработки, поиска и использования всего того, что нам удалось «узнать». Значит, с данными нужно что-то делать. Но «делать» – это означает, насколько возможно, сократить их количество и при этом не потерять слишком много «полезной информации», потенциально в них заложенной». Следовательно, классификация – это процедура упрощения массива данных (чтобы облегчить его экспертный анализ и содержательную интерпретацию).

Отметим, что существуют разные подходы к систематизации сложных многомерных объектов, которые определяются различными терминами: классификация, таксономия, кластеризация и др., причем общепринятого понимания в использовании этой терминологии на сегодня не существует. Правда, следует отметить, что количественная таксономия, компонентный [2] и кластерный анализ [3] не занимаются распределением объектов по априори заданным классам, что относится к задачам дискриминантного анализа [4], а устанавливают заранее неизвестную классификацию. Эта классификация, как правило, оказывается не единственной. И ее результаты крайне редко удается рассматривать как выявление объективной внутренней структуры, отражающей «фундаментальные» свойства изучаемой области знания [5].

Различают два принципиально разных подхода к систематизации: исключающие и неисключающие классификации. При исключающей классификации один объект может быть отнесен только к одному из классов (таксонов). При неисключающей классификации объект может быть отнесен к нескольким классам. Развитием идеи неисключающей классификации явилась теория нечетких (размытых, расплывчатых) множеств Л.А. Заде [6,7].

Исходная идея нечетких множеств самим Л. Заде была сформулирована следующим образом: «Для данного объекта 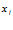и заданного класса 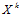в большинстве случаев вопрос состоит не в том, принадлежит ли
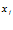к 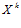, а в том, насколько
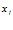принадлежит к 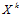» [6]. Для формализации этого взгляда на классификацию Л. Заде «размыл» индикатор принадлежности

,

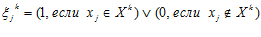заменив его лингвистической переменной [8] (или, как синоним, функцией нечеткой принадлежности), определяемой в виде 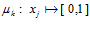. Таким образом, определяет меру принадлежности элемента 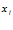заданному подмножеству 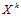, которая, подобно вероятности, не превосходит единицу.

Пример. Пусть 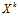– нечеткое множество «сторонники партии «Единая Россия» (ЕР). Некоторым образом установлено формальное правило, которое задает лингвистическую переменную (размытый индикатор принадлежности к этому нечеткому множеству). Гражданин 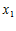стал членом партии ЕР и всегда участвовал в мероприятиях по ее поддержке. В этой связи оказалось, что 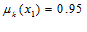. Господин 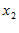в ЕР не состоит, но всегда голосовал за ЕР. Для него 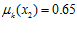. Субъект 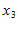на голосования и общественные мероприятия не ходил (было лень), но в кругу семьи он всегда говорил, что «Путин и Медведев - это намного лучше, чем коммунисты или национал-патриоты». Его лингвистическая переменная 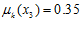. Товарищ 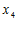всегда голосовал против ЕР и ее политики, в связи с чем: .

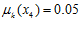Несложно заметить сходство лингвистической переменной μ с функцией плотности вероятностей (или самой вероятностью в дискретном случае). Есть и различие: функция распределения всегда нормирована к единице, а сумма S всех значений μ (или, в общем случае, интеграл Лебега от лингвистической переменной μ) может быть любым неотрицательным числом . Однако, несложно отнормировать сумму 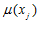к единице, просто разделив каждое значение лингвистической переменной на S. Таким образом, можно считать в достаточно общем виде, что и вероятность, и нечеткая принадлежность представляют собой меры, суммы которых нормированы к единице.

В этой связи уместно вспомнить, что в начале 80–х гг. ХХ в. среди советских специалистов, связанных со статистическим анализом данных социально–экономического характера, это обстоятельство привело к острой дискуссии : а «стоит ли» вообще рассматривать «нечеткие множества», если есть теория случайных множеств [9].

Дискуссия не привела «к консенсусу», вопрос актуален и сегодня. Например, в современных монографиях А.И. Орлова [10,11], известного и высококвалифицированного специалиста по прикладной статистике, содержится материал «о сведении нечетких множеств к случайным». Математически корректно А.И. Орлов показывает, каким образом нечеткие множества правомерно рассматривать как некоторые проекции случайных множеств (см., например, [11, п.4.6]). Формально сделанные выкладки правильны, но с содержательной точки зрения, как видится автору, взгляды А.И. Орлова неверны. Коротко остановимся на обсуждении этого вопроса.

Есть абстрактное множество Х и элемент 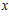. Мы не знаем точно, принадлежит ли 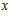к Х, но
можем оценить вероятность этого события 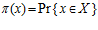. Пара 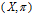, т.е. множество элементов 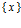с заданными вероятностями принадлежности 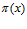, называется случайным множеством. Математически случайное множество является измеримым отображением одного вероятностного пространства на другое (как правило, само на себя).

Приведем несколько примеров случайных множеств.

(а) В геологических районах 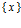по предварительным данным может быть нефть. По имеющимся косвенным признакам оценили вероятности этих событий 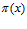. Набор пар 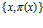образует случайное множество.

(б) Данные радиолокации противолодочного корабля показывают, что наблюдаемая цель 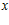с вероятностью 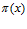является подводным крейсером США. Набор пар 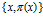также образует случайное множество.

(в) По результатам исследований (скажем, анализу ДНК) на основании некоторой методики оценивается вероятность 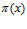того, что отцом данного ребенка является гражданин 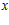. Набор пар 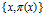– случайное множество.

Автору представляется очевидным, что по смыслу нечеткое множество не может рассматриваться как множество случайное. В рассмотренных случаях: (а) в данном районе либо есть нефть, либо нет; (б) данная подлодка или является крейсером США, или нет; (в) у ребенка есть только один отец. Следовательно, в реальности все указанные выше множества 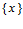являются обычными, а не размытыми (нечеткими, расплывчатыми) множествами.

А вероятность 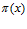появляется не в силу каких-то «фундаментальных» свойств элементов рассматриваемых множеств, а в силу нашей неполной информированности об этих множествах. Следовательно, в любом случайном множестве 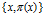вероятность 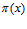служит не объективной характеристикой принадлежности х к Х, а мерой нашей осведомленности  об этом событии.

О вероятностях такого рода Анри Пуанкаре писал [12]: «Однако можно оставить в стороне слабость человеческой природы: то, что представляется случайным для человека необразованного, отнюдь не будет таковым для ученого. Случайность, таким образом, служит как бы мерой нашего невежества (курсив мой. – авт.)». Вывод: нет оснований подменять смысл лингвистической переменной мерой, описывающую степень субъективной информированности о принадлежности данного элемента к множеству.

Сравните: (а) Иванов «толстый» с мерой 0.9; (б) Петров «богат» с мерой 0.5; (в) Сидорова «красива» с мерой 0.1; (г) Козлов «храбр» с мерой 0.01. Это не характеристики нашей осведомленности о свойствах субъектов, а их объективные характеристики, выражаемые соответствующими предикатами. Которые, в данном конкретном случае, означают: (а) Иванов очень тучен; (б) материальное положение Петрова весьма среднее; (в) внешне Сидорова крайне непривлекательна, (г) Козлов патологически труслив.

Можно возразить: совершенно неясно, как задавать эти «объективные» характеристики. Ответ очевиден: по оговоренной методике. Это нормально, ведь и вероятности для случайных множеств вычисляются не по законам Божьим, а по некоторым когда-то и кем-то обоснованным методикам.

Замечание для математически подготовленного читателя: отметим, что вопросы унифицированного построения лингвистической переменной (т.е. оценки уровней принадлежности), как и ее измерения, были достаточно полно проработаны уже в 80-е гг. прошлого века (см., например, [13-18]).

Возвращаясь к точке зрения А.И. Орлова, отметим, что формально его выкладки безупречны, но их логика неверна. В рамках естественнонаучной традиции, ни при каких обстоятельствах нельзя красивую математическую абстракцию ставить выше содержательного смысла изучаемого явления.

Рассуждая по аналогии с позицией А.И. Орлова, и само понятие вероятность вводить незачем. Вполне достаточно рассматривать меру, нормированную к единице, на множестве с заданной на нем сигма – алгеброй. Но понятие вероятности несет колоссальную смысловую нагрузку, в связи с чем ее смысл в принципе не сводим к формальной мере на множестве. Тем более, что теоретико-множественное описание (а не определение !) вероятности по А.Н. Колмогорову – не единственно возможный путь строгой формализации понятия вероятности [19-26]. Причем понятие пространства элементарных событий, лежащее в основе аксиоматики А.Н. Колмогорова [27,28], – чистейшая абстракция. Кроме тривиальных случаев конечных множеств, в природе не существует объектов, адекватных этому понятию.

Ввиду важности вопроса для социально-экономических исследований, необходимо понять истоки самого понятия неопределенности, которое лежит в основе осознания человеком событий (наблюдений) с неясным исходом. Видимо, наиболее объективна точка зрения М. Гупта [29], считающего, что неопределенность бывает 2-х видов, связанных: 1) со стохастическим поведением изучаемой системы (т.е. случайностью, по сути дела) и 2) с низкой формализуемостью понятийных категорий, а также с ограниченными возможностями человеческих восприятий и рассуждений (по сути – с нечеткостью). В каждой неопределенности в этом мире (в том числе – в социально-экономических и социальных областях) всегда присутствует или случайность, или нечеткость, или их одновременное проявление.

Хотя, есть мнение, что разработки в области теории нечеткой меры [30], сделанные в связи с созданием основ теории возможностей Д. Дюбуа и А. Прадом [31] (еще одно мощное развитие идей Л.А. Заде), позволяют с некоторым оптимизмом смотреть на перспективы создания единой теории неопределенности. Правда, необходимо сразу подчеркнуть, что в понятном смысле теория возможностей является альтернативой теории вероятностей, поскольку выражает и случайность, и нечеткость только через меры нечеткости [32]. Таким образом, в рамках теории возможностей, случайность сводится к нечеткости. Тем самым реализуется прямая альтернатива тем формализованным взглядам А.И. Орлова, которые были рассмотрены выше. Понятно, что «возможностная» модель малопригодна в ситуациях, когда случайная составляющая преобладает в неопределенности, а «вероятностная» модель плохо описывает явления, где в неопределенности доминирует нечеткость.

Можно утверждать, что на сегодняшнем уровне развития математики бессмысленны любые попытки замены нечеткости случайностью и наоборот.

1. Адлер Ю.П.  Наука и искусство анализа данных // Предисловие к книге: Мостеллер Ф., Тьюки Дж. Анализ данных и регрессия. В 2-х томах / Пер. с англ. М.: Финансы и статистика, 1982.
2. Иберла К. Факторный анализ / Пер. с англ. М.: Статистика, 1980.
3. Дюран Б., Одел П. Кластерный анализ / Пер. с англ. М.: Статистика, 1977.
4. Бессокирная Г.П. Дискриминантный анализ для отбора информативных признаков // Социология: методология, методы, математические модели. 2003, 16, с. 142-153.
5. Трофимов В.П. Логическая структура статистических моделей. М.: Финансы и статистика, 1985.
6. Заде Л.А. Размытые множества и их применение в распознавании образов и кластер-анализе // Классификация и кластер. Сборник научных работ под ред. Дж. Вэн Райзина. / Пер. с англ. М.: Мир, 1980, с. 208-243.
7. Кофман А.. Введение в теорию нечетких множеств. М.: Радио и связь, 1982.
8. Заде Л.А. Понятие лингвистической переменной и его применение к принятию приближенных решений / Пер. с англ. М.: Мир, 1976.
9. Матерон Ж.  Случайные множества и интегральная геометрия / Пер. с англ. М.: Мир, 1978.
10. Орлов А.И. Нечисловая статистика. М.: МЗ - Пресс,  2004.
11. Орлов А.И.  Прикладная статистика. М.: Экзамен, 2006.
12. Пуанкаре А. Наука и метод // Пуанкаре Анри. О науке. Сборник избранных научных трудов. М.: Наука, 1990, с. 367-522.
13. Ягер Р.Р. Множества уровня для оценки принадлежности нечетких подмножеств // Нечеткие множества и теория возможностей. Последние достижения / Пер.с англ. Сб. научных трудов под ред. Ягера Р.Р. М.: Радио и связь, 1986, с.71-78.
14. Кузьмин В.Б. Эталонный подход к получению нечетких отношений предпочтения // Нечеткие множества и теория возможностей. Последние достижения / Пер.с англ. Сб. научн. тр. М.: Радио и связь, 1986, с.87-99.
15. Норвич А.М., Турксен И.Б. Фундаментальное измерение нечеткости // Нечеткие множества и теория возможностей. Последние достижения / Пер.с англ. Сборник научных трудов. М.: Радио и связь, 1986, с.51-63.
16. Норвич А.М., Турксен И.Б. Построение функций принадлежности // Нечеткие множества и теория возможностей. Последние достижения / Пер.с англ. Сборник научных трудов. М.: Радио и связь, 1986, с.64-70.
17. Борисов А.Н., Алексеев А.В. Обработка нечеткой информации в системах принятия решений. М.: Радио и связь, 1989.
18. Малышев Н.Г., Берштейн Л.С., Боженюк А.В. Нечеткие модели для экспертных систем в САПР. М.: Энергоатомиздат, 1991.
19. Мизес Р. Вероятность и статистика / Пер. с нем. М.- Л.: Госиздат, 1930.
20. Смирнов Н.В. Теория вероятностей и математическая статистика. Избранные труды. М.: Наука, 1970.
21. Постников А.Г. Арифметическое моделирование случайных процессов // Труды математич. инстит. АН СССР им. Стеклова, 1960, т, 57, с. 272-291.
22. Филиппова А.А. Теорема Мизеса о предельном поведении функционалов от эмпирических функций распределения и ее статистические применения // Теория вероятностей и ее применен., 1962, т. 7, № 1, с.187-196.
23. Устинов Ю.К. О понятии статистического пространства Мизеса // Математ. статистика и ее прилож., вып. Х. Томск: ТГУ, 1986, с. 212-218.
24. Тутубалин В.Н. Теория вероятностей. Краткий курс и научно-методические замечания. М.: МГУ, 1972.
25. Алимов Ю.И. Измерение спектров и статистических вероятностей. Свердловск: Уральский политехнический институт, 1986.
26. Алимов Ю.И., Кравцов Ю.А.  Является ли вероятность «нормальной» физической величиной? // Успехи физич. наук, 1992, т. 162, № 7, с.149-182.
27. Колмогоров А.Н. Общая теория меры и исчисление вероятностей. // Труды Коммунистич. академии, разд. математ., 1929, т.1, с.8-21.
28. Колмогоров А.Н. Основные понятия теории вероятностей. М.: Наука, 1974.
29. Gupta M.M. Cognition, perception and uncertanity // Fuzzy logic in knowledge-based systems, decision and control / Ed. M.M.Gupta, T.Yamakawa. – Elsevor Science Publishers B.V. – 1988. – P.3-10.
30. Клемент Э.Ф. О связи между различными понятиями нечетких мер // Нечеткие множества и теория возможностей. Последние достижения / Пер.с англ. Сборник научных трудов. М.: Радио и связь, 1986, с.279-285.
31. Дюбуа Д., Прад А. Теория возможностей. Приложение к представлению знаний в информатике / Пер. с фр. М.: Радио и связь, 1990.
32. Дюбуа Д., Прад А. К анализу и синтезу нечетких отображений // Нечеткие множества и теория возможностей. Последние достижения / Пер.с англ. Сборник научных трудов. М.: Радио и связь, 1986, с.229-240.

Все статьи автора «Черепанов Евгений Васильевич»