ОПТИМАЛЬНЫЙ СПОСОБ ОПРЕДЕЛЕНИЯ СУММЫ УГЛОВ В ТРЕУГОЛЬНИКЕ С ПОМОЩЬЮ ЦЕНТРАЛЬНОЙ СИММЕТРИИ

Обозначим середины отрезков АС, ВЕ, АВ, СЕ через М₁, М₂, М₃, М₄ соответственно (Рис. 2); середины отрезков определя­ют­ся как точки пересечения отрезков и серединных перпен­дикуляров к ним.

Применим к отрезку АС центральную симметрию с центром симметрии в точке С. Образом точки А относительно центра симметрии С станет точка Н; при этом, по определению цент­рально симметричных точек (Def. 7.4.2.), точки А, С и Н лежат на одной прямой, отрезок АС равен отрезку СН (Рис. 2). Образом точки М₁ относительно центра симметрии С станет точка М₅; при этом, по определению центрально симметричных точек (Def. 7.4.2.), точки М₁, С и М₅ лежат на одной пря­­мой – прямой АС, отрезок М₁С равен отрезку СМ₅ (Рис. 2).

Применим к отрезку ОМ₄ центральную симметрию с центром симметрии в точке М₄. Образом точки О относительно центра симметрии М₄ станет точка О₂; при этом, по определению цент­рально симметричных точек (Def. 7.4.2.), точки О, М₄ и О₂ лежат на одной прямой, отрезок ОМ₄ равен отрезку М₄О₂ (Рис. 2).

Применим к треугольнику ЕСВ центральную симметрию с центром симметрии в точке М₄. Образом точки В будет точка Н, что будет доказано далее, образом треугольника ЕСВ при центральной симметрии относительно точки М₄ будет треугольник СЕН (Рис. 2): . По теореме 7.1.1. о сохранении расстояний между двумя точками при центральной симметрии: СН = ЕВ, ЕН = СВ, следовательно, треугольник СЕН равен треугольнику ЕСВ по трем сторонам (Ах. 8.5.3.). По аксиоме о равенстве фигур (Ах. 6.8.), угол ЕСН равен углу СЕВ, равному углу ВАС.

Предположим, что образом точки В относительно центра симметрии М₄ будет некоторая точка D, отличная от точки Н. Если точка D лежит на прямой АС, то CD≠ЕВ=с, следова­тельно, треугольники СЕD и ЕСВ не равны. Если точка D не лежит на прямой АС (Рис. 3), то .

По аксиоме 4.7.2. об аддитивности прилегающих углов: , то есть  при условии, что . Тогда образом точки О относительно центра симметрии М₄ будет точка О₃, отличная от точки О₂, следовательно: или, или точка О₃ не лежит на прямой ОМ₄, что противоречит определению центрально симметричных точек (Def. 7.4.2.). Предположение о том, что образом точки В относительно центра симметрии М₄ является точка D, отличная от точки Н, приводит к противоречию, следовательно, оно неверно, следо­вательно, образом точки В относительно центра симметрии М₄ является точка Н.

Углы АСВ, ВСЕ и ЕСН образуют развернутый угол АСН (Рис. 2), следовательно, сумма величин углов треугольника АВС: ,  и  равна π (Def. 4.11.).

На рисунках 1–2 представлен остроугольный треу­гольник. Рассмотрим произвольный тупоугольный треуголь­ник АВС. Середину его стороны ВС обозначим через О. Применим к тре­угольнику АВС цент­ральную симмет­рию с центром симмет­рии в точке О (Рис. 4); середина отрезка определяется как точка пересечения отрезка и серединного перпен­дикуляра к нему. Точки В и С симметричны относительно центра симметрии – точки О; образом точки А относительно центра симметрии О является точка Е (Рис. 4). Соединяем отрезками точку Е с точками В и С, образуется треугольник ЕСВ. Треугольник ЕСВ является образом треугольника АВС отно­сительно центра симметрии – точки О. По теореме 7.1.1. о сохранении расстояний между двумя точками при центральной симметрии, отрезок ЕС равен отрезку АВ, отрезок ЕВ равен отрезку АС, следовательно, треугольник ЕСВ равен треугольнику АВС по трем сторонам (Ах. 8.5.3.). Угол ЕСВ равен углу АВС, угол СЕВ равен углу ВАС – по аксиоме о равенстве фигур (Ах. 6.8.).

Применим к треугольнику ЕСВ центральную симметрию с центром симметрии в точке М₄ – середине отрезка СЕ. Образом треугольника ЕСВ при центральной симметрии относительно точки М₄ будет треугольник СЕН (Рис. 5): . По теореме 7.1.1. о сохранении рассто­яний между двумя точками при центральной симметрии: СН = ЕВ, ЕН = СВ, следовательно, треугольник СЕН равен треугольнику ЕСВ по трем сторонам (Ах. 8.5.3.). По аксиоме о равенстве фигур (Ах. 6.8.), угол ЕСН равен углу СЕВ, равному углу ВАС.

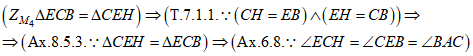
Углы АСВ, ВСЕ и ЕСН образуют развернутый угол АСН (Рис. 5), следовательно, по определению развернутого угла (Def. 4.11.), сумма величин углов треугольника АВС: ,  и  равна π.

Рассмотрим произвольный прямоугольный треугольник АВС. Середину его стороны ВС обозначим через О. Образом треу­гольника АВС отно­сительно центра симметрии О является треугольник ЕСВ (Рис. 6). По теореме 7.1.1., ЕС = АВ, ЕВ = АС, следовательно, треугольник ЕСВ равен треугольнику АВС по трем сторонам (Ах. 8.5.3.). По аксиоме 6.8. о равенстве фигур, угол ЕСВ равен углу АВС, угол СЕВ равен углу ВАС.

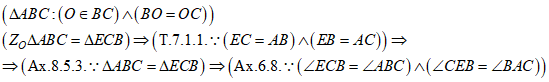
Образом треугольника ЕСВ при центральной симметрии относительно точки М₄ – середины отрезка СЕ – будет треугольник СЕН (Рис. 7): . По теореме 7.1.1. о сохранении рассто­яний между двумя точками при центральной симметрии: СН = ЕВ, ЕН = СВ, следовательно, треугольник СЕН равен треугольнику ЕСВ по трем сторонам (Ах. 8.5.3.). По аксиоме о равенстве фигур (Ах. 6.8.), угол ЕСН равен углу СЕВ, равному углу ВАС.

Углы АСВ, ВСЕ и ЕСН образуют развернутый угол АСН (Рис. 7), следовательно, сумма величин углов треугольника АВС: ,  и  равна π (Def. 4.11.).

Для тупоугольного и прямоугольного треугольников построе­ния выполняются так же, как и для остроугольного треугольника, то есть независимо от расположения тупого или прямого угла по отношению к выбранному основанию треугольника.
Сформулируем теорему: Сумма величин внутренних углов в треугольнике равна π. Теорема доказана.

Выводы. Сумма внутренних углов в произвольном треугольнике, равная π, определена с помощью центральной симметрии оптимальным способом – композицией двух центральных симметрий. Использование центральной симметрии является независимым способом определения суммы углов в треугольнике, то есть не использующим аксиому о параллельных прямых, что очень важно для доказательности классической геометрии.