MODELING OF ATMOSPHERIC POLLUTION BIOGAS FROM LANDFILLS WITH BY MEANS OF SOLUTIONS OF THE EQUATIONS OF TURBULENT DIFFUSION AND THE NAVIER-STOKES EQUATIONS

The decomposition of waste in landfills is produced biogas is a gas – a mixture of hydrocarbons, carbon dioxide, hydrogen sulfide, xylene, ammonia and other chemical substances. Some of components are toxic and inflammable. The environmental danger of dissipation of biogas is caused by the contamination of adjacent to the test site territory. Known methods of calculation of the field of concentrations of impurities, such as OND-86 (used in the countries-republics of the former USSR), normal (Gaussian) distribution are in most parts of approximations, and do not consider in detail processes taking place in the flow of the stream of obstacles, which are the buildings, the structures themselves and polygons, which are of substantial size and who can significantly influence convective and turbulent transport processes impurities.

The paper presents the numerical simulation of the dispersion of biogas from landfills using the solutions of the equations of diffusion and Navier-Stokes equations. The results can be used for the assessment of the pollution of the atmospheric air in the area of influence of landfill sites, in choosing the location of future landfill, in substantiation of the size of the sanitary protection zones of landfill, remediation and evaluation of the effectiveness of measures to reduce air pollution biogas.

For modeling of the dispersion of biogas invited to the numerical solution of differential equations of convective-diffusion transfer of contaminants in the atmospheric air, which has the form:

here u, v, w are wind velocity components along the axes x, y, z; k_x, k_y, k_z are coefficients of the turbulence along the axes х, у, z;

  I(r, t) is function of the emission of pollutants. To simplify the calculations in the future in equation (1) and accounting of emission of biogas is produced with the help of boundary conditions – concentration on the surface of landfill [4].

Coefficients of turbulence it is expedient to define by means of Smagorinsky model that takes into account the additional turbulence caused by the vorticity, with the help of equations [3]:

here 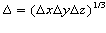is the scale of the smaller eddies is determined by the width of three-dimensional cell, k_based is the basic coefficient of turbulence, is determined as:

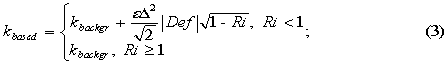
here k_backgr is background coefficient of turbulence, k_backgr=1-15 м²/с; ε=0,1-0,4;

Def(x; y; z; t) is the function of dissipation or deformation, which is determined using the equation:

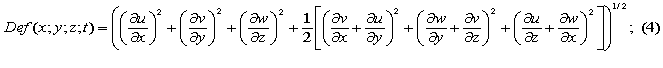
 Ri is local number Richardson, which is determined using equation:

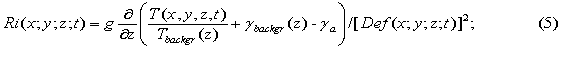
here T is the temperature; γ_backgr(z) is the gradient of temperature background, γ_а is adiabatic temperature gradient.

Thermal imaging survey of various landfills, which was made by author in [5] showed that release of biogas at landfill can be considered “cold”, i.e.:

here Т_biogas is the temperature of the exhaust of biogas; Т_backgr is background temperature.

In modeling dispersion of emissions from low sources of greatest interest is the lower boundary of the surface layer of the atmosphere, to which the lower 50-100 m in it vertical fluxes of heat and momentum are constant in height and are resistant to the atmosphere. Given small vertical extent of the layer, you can take the equilibrium condition (indifferent) stratification, when the vertical heat flux is zero, and temperature change occurs adiabatically. [1] In this case, the vertical temperature gradient is adiabatic g_a = 0,01ºC per meter.

For neutral stratification of the atmosphere of “cold” emissions

And system (3) is simplified:

Rough, chemically active surface capable of partial retention of biogas on the surface with further absorption. Under aerobic processes in biogas composition dominates the carbon dioxide absorbed during photosynthesis. The rest of the components poison soils and plants. Diffusion of gas at the “air-to-ground” can be expressed by equation:

here β is constant of interaction (for smooth, chemically inert surface β≈0).

At the initial moment of time (without background) concentrations of impurities of biogas are equal to zero. The infinite distance from the landfill of impurity concentration is equal to zero:

For modeling of turbulent motion of the gas is used direct modeling «DNS», based on the decision of non-stationary Navier-Stokes equations for incompressible fluids and gases:

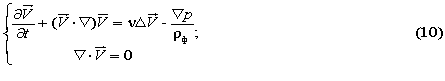
here ν is the kinematic viscosity, p is pressure,

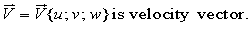
For the free stream pressure p equals the atmospheric, v=w=0, the profile of wind speeds at neutral stratification of atmosphere is described by Karman [3]:

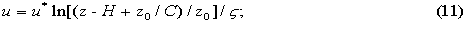
here H is average height of wind obstructions (buildings, forest plantations); C is coefficient of resistance. Values ​​of z₀ and C for some surfaces are given in Table 1.

Table 1 – The values of z₀ and C for some types of surfaces [3]

Wind velocity profile is also convenient to define the equation, use the simulation in wind tunnels [3]:

here u* is dynamic speed, m/s; ϛ is constant Karman, ϛ = 0,4; z₀ is the desired height; u₀ is the speed of the wind at a given height z₀.

To solve the problems associated with the transfer of turbulent scalar substances in solution of differential equations using the scheme of splitting into physical processes. According to the principles of splitting finite-difference integration of the equations of hydrodynamics and convective-diffusive transport of scalar substance at each time step Dt is carried out in two stages. At the first stage the hydrodynamic parameters. In the second phase, based on the calculated hydrodynamic fields solved the diffusion equation.

As an example, we present dispersion modeling of methane (main component of biogas) in the landfill “Centralny” of Volgograd region of Russian Federation in 2007. The modeling was made in the software environment «Mat lab / Femlab». Profile free-stream passed logarithmic, values ​​ k_backgr=4 m²/s; ε=0,2. In Figure 1 we show the velocity field of the wind and concentrations of methane.

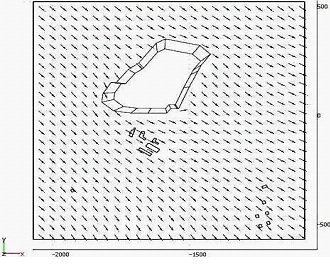
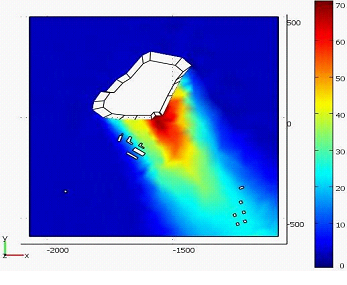
Figure 1 – The velocity field of the wind flow around the polygon (left) and the field of methane in the landfill area of ​​influence “Central” (right)

Table 2 – Comparison of values of concentration of methane in the zone of influence of the landfill «Central» in 2007, received a variety of ways

So, modeling based on the solutions of Navier-Stokes equations and diffusion yielded result is significantly better than the method OND-86. The results of calculation using the proposed model are close to experimental data. Modeling emissions of biogas on stage at the stage of operation, reclamation landfills can be considered as an aspect of information modeling, to ensure environmental safety in the handling of waste.

1. Батракова Г.М., Бояршинов М.Г., Горемыкин В.Д. Моделирование переноса и рассеивания атмосферном воздухе метана, эмитированного с территории захоронения твёрдых бытовых отходов // Вестн. Воронежского ун-та. Геология. – 2005. – № 1.– С. 256-261.
2. Берлянд М.Е. Современные проблемы атмосферной диффузии и загрязнения атмосферы. – Л.: Гидрометеоиздат, 1975. – 448 с.
3. Дацюк Т.А. Моделирование рассеивания вентиляционных выбросов. – Спб: СПБГАСУ, 2000. – 210 с.
4. Сауц А.В. Граничные условия численного моделирования рассеивания биогаза над полигоном // Инженерно-экологические системы: материалы междунар. конгресса, посвящённого 180-летию СПБГАСУ. – СПб: СПБГАСУ, 2012. – С. 155-158.
5. Сауц А.В. Об энергетическом обследовании возобновляемых источниках энергии. Тепловизионное обследование полигонов ТБО и ПО // Технологии энергосбережения. Статьи экспертов. – 2013. URL: http://spbtes.ru/expert/ob-energeticheskom-obsledovanii-vozobnovlyaemyh-istochnikov-energii-teplovizionnoe (date accessed: 26.03.2013).
6. Сауц А.В. Обоснование санитарно-защитных зон полигонов твёрдых бытовых и промышленных отходов при их строительстве и эксплуатации // Вестник гражданских инженеров. – 2012. – № 4(33) – С. 200-202.

All articles of author «artursauc»