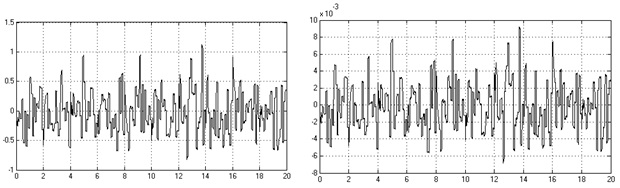
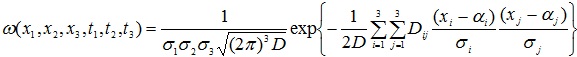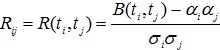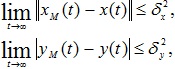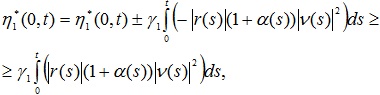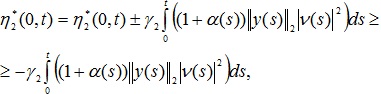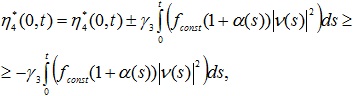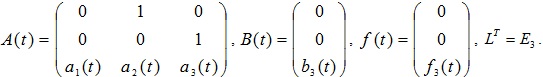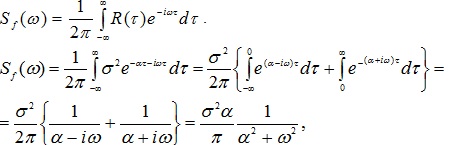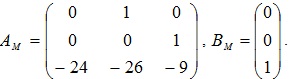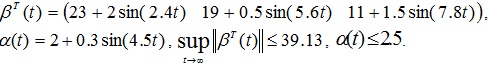Во многих случаях характер воздействия на системы автоматического регулирования бывает таким, что его нельзя считать определенной функцией времени. Оно может принимать с течением времени самые разнообразные случайные значения. В таких случаях можно оценить только вероятность появления той или иной формы воздействия в тот или иной момент времени [2]. Это происходит не потому, что оно неизвестно заранее, а потому, что сама природа реального задающего или возмущающего воздействия такова, что величина его в каждый момент времени и процесс его изменения с течением времени зависят от множества разнообразных величин, которые случайным образом могут комбинироваться друг с другом, появляться одновременно или с любым сдвигом во времени и т. д.
Рассмотрим нестационарный объект управления, динамические процессы которого описываются уравнениями (1) с относительной степенью передаточной функции n-m=1.
(1)
где 
– вектор переменных состояния; 
– вектор выхода объекта; 
– обобщенный выход объекта, формируемый с помощью линейного компенсатора 
; 
– управление; – нестационарная квадратная матрица состояния размерности
; – нестационарный вектор размерности
; – матрица выхода размерности
; 
– случайная вектор-функция внешних возмущений или помех, относительная степень объекта (n-m)=1.
На объект (1) действует случайное воздействие в виде гауссовского процесса. Его многомерная функция распределения, для совокупности значений 
определяется выражением
,
где 
- среднее значение и дисперсия процесса в момент времени 
, 
- определитель n-го порядка корреляционной матрицы, 
- алгебраическое дополнение элемента
.
Желаемое поведение объекта управления (1) задается с помощью явно-неявной эталонной модели:
, (2)
где 
– вектор выхода эталонной модели (ЭМ); 
– обобщенный выход ЭМ; 
– линейный компенсатор; 
– скалярное задающее воздействие; 
– стационарная квадратная матрица состояния размерности , причем 
является гурвицевой; 
– стационарный вектор размерности .
Будем считать, что выполнены условия структурного согласования между объектом (1) и эталоном вида (2):
, (3)
где 
– нестационарный вектор, ограниченный по норме; 
– скалярная функция времени.
Требуется построить робастную систему управления с явно-неявной эталонной моделью (2) таким образом, чтобы при любом наборе 
, при любых начальных условиях 
и ограниченных возмущениях выполнялось целевое условие:
(4)
где 
– некоторые относительные малые числа.
Матрица является гурвицевой, т.е. ее собственные значения удовлетворяют соотношению:
(5)
В таком случае передаточную функцию W(s) можно преобразовать с учетом соотношения (5) к виду:
.
Тогда необходимо и достаточно вектор 
выбрать таким образом, чтобы полином 
был гурвицевым степени 
с положительными коэффициентами, что гарантировало бы выполнение условия 
, 
.
Рассмотрим модификацию интегрального неравенства Попова (МИНП)
(6)
где 
– положительно определенные функции; hi*(0,t), i =1, 2, 3, 4 – модифицированные интегральные слагаемые вида:
(7)
(8)
(9)
(10)
где 
– корреляционная функция гауссовского случайного процесса, 
- дисперсия процесса, 
определяет корреляцию (статистическую зависимость) соседних чисел.
Оценки для интегралов (7), (8) и (10) имеют вид:
(11)
(12)
(13)
где введены следующие постоянные коэффициенты 
; 
; 
.
– оценка спектральной плотности 
случайной функции f(t). Данная формула называется формулой Винера-Хинчина.
Явный вид закона управления описывается следующей формулой
(14)
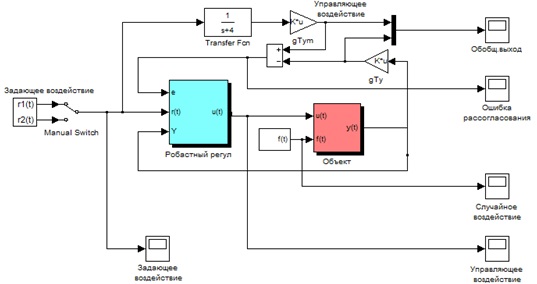
Структурная схема робастной системы управления (1), (2), (3), (14) представлена на рисунке 1.
Рисунок 1 – Структурная схема робастной системы управления
нестационарным объектом с действием случайной помехи с ЯНЭМ
Проведем имитационное моделирование системы нелинейного робастного управления нестационарным объектом с действием случайной помехи с ЯНЭМ. Рассмотрим систему, описываемую уравнениями (1), (3), (14), в которой параметры объекта управления и эталонной модели (2) в векторно-матричной форме имеют значения
Коэффициенты объекта изменяются по законам:
Определим спектральную плотность 
гауссовского случайного процесса по формуле
то есть в этом случае 
Эталонная модель задана в виде:
Синтез системы с явно-неявной эталонной моделью связан с выбором компонент вектора g для обеспечения условия положительности ЛСЧ вида:
согласно которой были получены компоненты вектора 
.
Нестационарные параметров объекта управления заданы в виде:
Задающие воздействия были сформированы следующим образом:
Параметры робастного регулятора (16) заданы как:
Имитационное моделирование осуществляется при помощи входящего в состав математического пакета MATLAB средства визуального моделирования SIMULINK.
Случайное воздействие реализовано с помощью блока Random Number (рисунок 2).
Рисунок 2 – Реализация случайного воздействия
с помощью блока Random Number
Структурная схема нестационарного объекта представлена на рисунке 3.
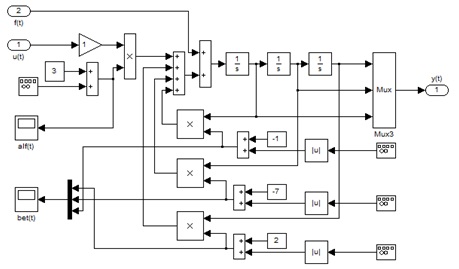Рисунок 3 – Реализация нестационарного объекта
Структурная схема робастного регулятора представлена на рисунке 4.
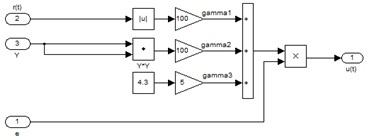Рисунок 4 – Реализация робастного регулятора
Разработанная система представляет собой пакет программ, состоящий из следующих m-файлов.
Файл interfeis.m – файл запуска системы. Данный файл запускает программу и предлагает пользователю осуществить выбор необходимого случайного воздействия (рисунок 5).
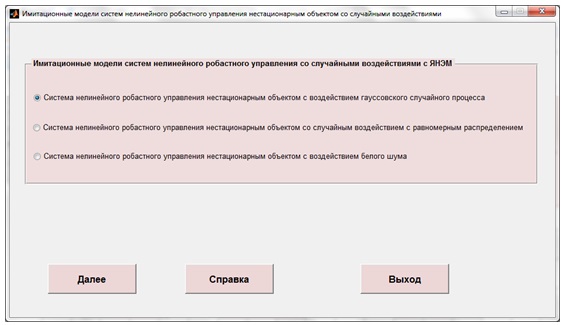Рисунок 5 – Главное окно программы
Для каждой из моделируемых систем внешний вид окна будет отличаться лишь заголовком окна и набором параметров модели. Внешний вид окна управления моделированием показан на рисунке 6.
Рисунок 6 – Окно управления моделированием
Файл help.m – запускает окно, содержащее всю справочную информацию, доступную пользователю.
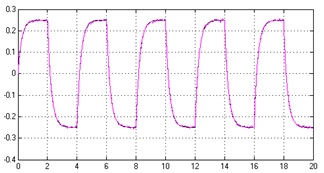
Результаты проведенного имитационного моделирования представлены на рисунках 7, 8, 9.
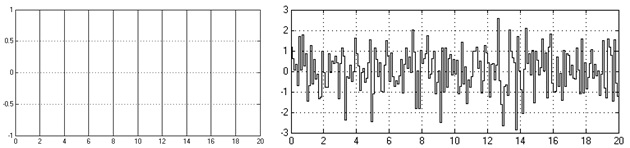Рисунок 7 – Задающее и случайное воздействия
Рисунок 8 –Выходы объекта и эталона для системы
Рисунок 9 – Управление и ошибка рассогласования для системы
Библиографический список
- Борисевич, А.В. Теория автоматического управления: элементарное введение с применением MATLAB / А.В. Борисевич. – СПб.: Политехнический ун-т, 2011. – 200 с.
- Бесекерский, В.А. Теория систем автоматического управления / В.А. Бесекерский, Е.П. Попов. – 4-е изд., перераб. и доп. – СПб.: Профессия, 2003. – 752 с.
- Гмурман, В.Е. Теория вероятностей и математическая статистика: учеб. пособие / В.Е. Гмурман. – 9-е изд., перераб. и доп. – М.: Высшая школа, 2003. – 479 с.
- Еремин, Е.Л. Нелинейное робастное управление сложными динамическими объектами / Е.Л. Еремин, Н.В. Кван, Н.П Семичевская, Д.А. Теличенко. – Благовещенск: Амурский гос. ун-т, 2011. – 204 с.