При разработке реальных систем обычно доминирует математический уровень строгости, и математический язык рассматривается как наилучшее средство представления системы. В большинстве работ ограничиваются лишь постановкой и исследованием математических задач и не затрагиваются содержательные и человеческие аспекты практической идентификации. Подобная избирательность во многом определяется тем, что при значительном объеме представлений о потенциально возможных способах исследователь не в состоянии разработать детальную общую схему идентификации.
При структурной идентификации определяется вид математической модели. Далее осуществляется параметрическая идентификация: определяются числовые параметры математической модели, при которых решение задачи соответствует экспериментальным данным. Обычно взаимодействие различных составляющих динамической системы задаются в виде систем алгебраических, дифференциальных (разностных), алгебро-дифференциальных или интегральных уравнений. В силу неоднозначности в постановке задачи (связана с неполнотой знаний об объекте, ограничениями в наблюдениях объекта во времени, неточностью измерения сигналов на входе и на выходе объекта и т. п.) выбор метода идентификации определяется неоднозначно.
Таким образом, выделяются следующие основные этапы идентификации:
– выбор структуры модели по результатам изучения системы или по имеющимся априорным сведениям;
– определение критерия близости (подобия) модели и системы;
– определение по экспериментальным данным, исходя из выбранного критерия, параметров модели.
Совокупностью критериев качества ![]() определяется качество целостной системы. Каждый из критериев
определяется качество целостной системы. Каждый из критериев ![]() есть численная (редко качественная) величина и характеризует способность удовлетворить установленные и/или предполагаемые потребности.
есть численная (редко качественная) величина и характеризует способность удовлетворить установленные и/или предполагаемые потребности.
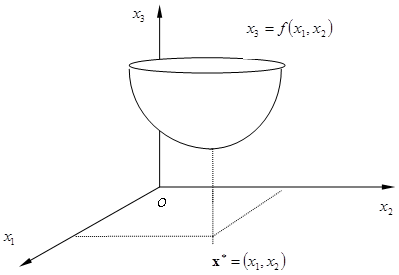
Ограничимся рассмотрением приложения методов теории сложных систем к синтезу композиционных материалов (определение оптимальных рецептурно-технологических параметров материала, обеспечивающих его структуру и свойства), а именно важной для практических приложений задачи определения минимума функции двух переменных:
точка ![]() принадлежит плоскости
принадлежит плоскости ![]() ; ось
; ось ![]() перпендикулярна плоскости
перпендикулярна плоскости ![]() (рис. 1). Уравнению
(рис. 1). Уравнению ![]() а некоторой окрестности точки
а некоторой окрестности точки ![]() локального минимума
локального минимума ![]() соответствует поверхность (имеет форму чаши) в трехмерном пространстве.
соответствует поверхность (имеет форму чаши) в трехмерном пространстве.
Если функция ![]() мономодальна в
мономодальна в ![]() (имеет единственную точку локального минимума
(имеет единственную точку локального минимума ![]() ) , то ее линии уровня
) , то ее линии уровня ![]() располагаются так, как это показано на рис. 2.
располагаются так, как это показано на рис. 2.

При множестве изолированных точек минимума функции будут мультимодальными.
В соответствии с предыдущим поиск точек ![]() локального минимума функции
локального минимума функции ![]() сводится к определению последовательности точек
сводится к определению последовательности точек ![]() , сходящейся к точке
, сходящейся к точке ![]() ; справедливо:
; справедливо:
Во всех методах спуска сначала выбирается начальная точка последовательности ![]() ; следующие приближения
; следующие приближения ![]() определяются соотношениями
определяются соотношениями
![]() , (1)
, (1)
где ![]() – вектор направления спуска; скалярная величина
– вектор направления спуска; скалярная величина ![]() является решением задачи одномерной минимизации
является решением задачи одномерной минимизации
![]() (2)
(2)
Поиск минимума функции нескольких переменных сводится к решению ряда задач одномерной минимизации (2) по переменной ![]() на отрезках
на отрезках ![]() -мерного пространства, проходяших через точки
-мерного пространства, проходяших через точки ![]() в направлении векторов
в направлении векторов ![]() . Методы спуска различаются лишь выбором вектора спуска и способом решения задачи одномерной минимизации. Для поиска минимума функции одной переменой можно ограничиться методом сканирования: выбрав произвольно начальную точку
. Методы спуска различаются лишь выбором вектора спуска и способом решения задачи одномерной минимизации. Для поиска минимума функции одной переменой можно ограничиться методом сканирования: выбрав произвольно начальную точку ![]() и начальный шаг по переменной t, можно получить различные точки минимума мультимодальной функции. Если функция
и начальный шаг по переменной t, можно получить различные точки минимума мультимодальной функции. Если функция ![]() мономодальна, то независимо от выбора начальной точки траектория поиска приведет к единственной точке локального минимума этой функции.
мономодальна, то независимо от выбора начальной точки траектория поиска приведет к единственной точке локального минимума этой функции.
Существует и другой метод поиска - покоординатный спуск Гаусса-Зейделя. Здесь ![]() в области определения функции
в области определения функции ![]() произвольно выбирается начальная точка. Приближения
произвольно выбирается начальная точка. Приближения ![]() определяются соотношениями (1), где
определяются соотношениями (1), где ![]() – единичный вектор, совпадающий с каким-либо координатным направлением. Например, если
– единичный вектор, совпадающий с каким-либо координатным направлением. Например, если ![]() параллелен
параллелен ![]() , то
, то ![]() = 1, 0, 0, …0, если он параллелен
= 1, 0, 0, …0, если он параллелен ![]() , то
, то ![]() = 0, 1, 0, …0 и т.д. Величина
= 0, 1, 0, …0 и т.д. Величина ![]() является решением задачи одномерной минимизации (2) и может определяться методом сканирования.
является решением задачи одномерной минимизации (2) и может определяться методом сканирования.
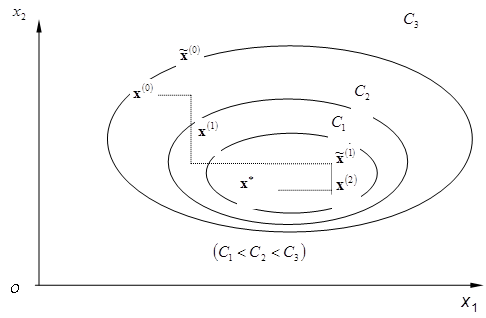
В частности, для функции двух переменных, исходя из начальной точки ![]() , можно определить точку
, можно определить точку ![]() минимума функции одной переменной
минимума функции одной переменной ![]() ;
; ![]() , а затем -точку минимума
, а затем -точку минимума ![]() функции
функции ![]() по второй координате. Принимая исходной точкой
по второй координате. Принимая исходной точкой ![]() (при фиксированной ее второй координате), определится точка минимума
(при фиксированной ее второй координате), определится точка минимума ![]() функции
функции ![]() одной переменной
одной переменной ![]() ;
; ![]() . Точка
. Точка ![]() определится в результате минимизации целевой функции
определится в результате минимизации целевой функции ![]() по координате
по координате ![]() (фиксируется координата
(фиксируется координата ![]() точки
точки ![]() ) и т.д. (рис.3).
) и т.д. (рис.3).
Вычислительная процедура прекращается при
![]() , (3)
, (3)
ε - заданная точность.
В методе наискорейшего спуска, исходя из начальной точки ![]() , строится последовательность приближений
, строится последовательность приближений ![]() , где
, где ![]() – единичный вектор, сонаправленный с направлением вектора-градиента функции
– единичный вектор, сонаправленный с направлением вектора-градиента функции ![]() в точке
в точке ![]() :
:
.gif) .
.Точку ![]() определяют из решения задачи одномерной минимизации функции
определяют из решения задачи одномерной минимизации функции ![]() по переменной t в направлении вектора
по переменной t в направлении вектора ![]() :
:
![]() . (6)
. (6)
Задача (4) численно легко решается методом сканирования. Вычислительная процедура осуществляется до выполнения неравенства (3).
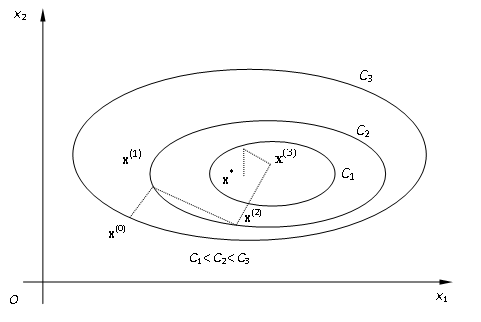
В двумерном случае отрезок ломаной, соединяющий точки ![]() и
и ![]() (k= 0, 1, …), параллелен вектору-градиенту функции
(k= 0, 1, …), параллелен вектору-градиенту функции ![]() в точке
в точке ![]() , перпендикулярному линии уровня функции
, перпендикулярному линии уровня функции ![]() , проходящей через точку
, проходящей через точку ![]() (рис.4).
(рис.4).
Приведенные методы эффективно использовались при определении рецептурно-технологических параметров строительных материалов различного назначения [1…7].
Библиографический список
- Математические методы в строительном материаловедении: монография / И.А.Гарькина [и др.]; под ред. акад. РААСН В.И.Соломатова. – Саратов: Изд-во Сарат. ун-та. – 2001. – 188 с.
- Данилов А.М.,Гарькина И.А., Домке Э.Р. Математическое и компьютерное моделирование сложных систем. – Пенза: ПГУАС. – 2011. – 296 с.
- Гарькина И.А., Данилов А.М., Домке Э.Р. Промышленные приложения системных методологий, теорий идентификации и управления / Вестник МАДИ. – 2009. – № 2(17). – С.77-82.
- Данилов А.М. Системы и модели: монография. – Пенза: ПГАСИ. –1995. – 200 с.
- Будылина Е. А., Гарькина И. А., Данилов А.М. Моделирование с позиций управления в технических системах / Региональная архитектура и строительство. –2013. – № 2 (16). – С. 138-142.
- Данилов А.М., Гарькина И.А. Методология проектирования сложных систем при разработке материалов специального назначения / Известия ВУЗов. Строительство.–2011. –С.80-85
- Данилов А.М., Гарькина И.А. Интерполяция, аппроксимация, оптимизация: анализ и синтез сложных систем: монография. – Пенза: ПГУАС. –2014. – 168 с.
