Математическая модель БИНС
Алгоритмы БИНС подробно описаны в работах как отечественных, так и зарубежных авторов, например, [6, 33, 36, 42]. Алгоритм навигации служит для определения положения центра масс подвижного объекта относительно земной системы координат. Для решения задачи навигации используются данные об ускорении объекта, измеренные акселерометрами в связанной системе координат.
Основная идея инерциальной навигации – это двукратное интегрирование измеренных ускорений. Способом построения БИНС является размещение инерциальных датчиков акселерометров и гироскопов непосредственно на борту подвижного объекта, а функции гиростабилизированной платформы, привязанной к земной системе координат, выполняет бортовой вычислитель.
Алгоритм БИНС основан на кинематических уравнениях подвижного объекта в земной системе координат:
|
(2.1)
|
где VZg, VXg – составляющие линейной скорости объекта соответственно вдоль оси Zg и Xg географической системы координат;
U – угловая скорость вращения Земли;
ц – широта местоположения объекта;
R – средний радиус земного эллипсоида.
На основе (2.1) угловая скорость движения объекта относительно Земли определяется следующими соотношениями:
|
(2.2)
|
Для получения координат объекта ц, л, h в географической системе необходимо иметь информацию о линейных скоростях объекта VXG, VYG, VZG. Эту информацию получают путем интегрирования соответствующих ускорений. В БИНС датчики ускорений – акселерометры устанавливают по осям связанной системы координат, они измеряют кажущееся ускорение. Следует отметить, что абсолютное ускорение имеет следующие составляющие:
|
|
(2.3)
|
где ap , ak , ao – составляющие ускорения соответственно переносного, кариолисова, относительного.
Кариолисово ускорение возникает при взаимодействии переносной угловой скорости вращения Земли и линейной скорости объекта. Проекции кариолисова ускорения на оси OXgYgZg имеют вид:
|
(2.4)
|
Относительное ускорение возникает при движении объекта вокруг Земли и при изменении линейной скорости, его составляющие на оси OXgYgZg имеют вид:
|
(2.5)
|
Переносное ускорение вызвано угловой скоростью вращения Земли, и его составляющие в пересчете в земную систему координат определяются соотношениями:
|
(2.6)
|
Акселерометры, жестко установленные в связанной системе координат, измеряют проекции кажущегося ускорения, в которых учитываются все три составляющие: кариолисово, относительное и ускорения силы тяжести. Путем пересчета кажущегося ускорения в географическую систему координат получают составляющие nXg, nYg, nZg:
|
(2.7)
|
где ![]()
![]() ,
, ![]()
![]() – составляющие ускорения объекта соответственно по осям Zg , Yg ,Xg географической системы координат.
– составляющие ускорения объекта соответственно по осям Zg , Yg ,Xg географической системы координат.
Для использования в навигационном алгоритме БИНС показаний акселерометров из них необходимо извлечь ![]()
![]() ,
, ![]()
![]() – составляющие ускорения объекта соответственно по осям Zg, Yg, Xg географической системы координат путем удаления из них вредных составляющих: ускорения Кариолиса, относительного ускорения и ускорения силы тяжести.
– составляющие ускорения объекта соответственно по осям Zg, Yg, Xg географической системы координат путем удаления из них вредных составляющих: ускорения Кариолиса, относительного ускорения и ускорения силы тяжести.
|
(2.8)
|
где ДnZg, ДnYg, ДnXg – вредные составляющие: ускорения Кариолиса, относительного ускорения и ускорения силы тяжести соответственно по осям Zg, Yg , Xg географической системы координат:
|
(2.9)
|
Навигационный алгоритм БИНС при интегрировании соотношений (2.8) вычисляет составляющие линейных скоростей:
|
(2.10)
|
где VZg(t0), VYg(t0), VXg(t0) – составляющие вектора скорости в начальный момент времени t0.
Угловые координаты объекта и высота определяются при вторичном интегрировании (2.2) с учетом начальных значений координат и высоты:
|
(2.11)
|
где ц0, л0, h0 – составляющие координат объекта в начальный момент времени t0.
Навигационный алгоритм БИНС, основанный на приведенных формулах, представлен на рис. 2.1 в виде структурной схемы [33].
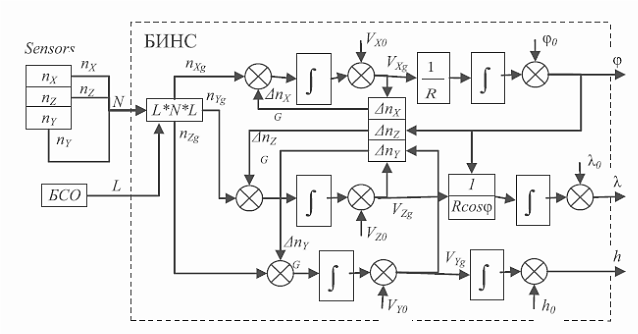 Рис. 2.1. Структурная схема алгоритма БИНС
Рис. 2.1. Структурная схема алгоритма БИНСМоделирование БИНС в среде Matlab Simulink.
Навигационный алгоритм БИНС, основанный на выражениях 2.1-2.11, представленный на рис. 2.1 в виде структурной схемы содержит конвертор вектора кажущегося ускорения с акселерометров для пересчета в земную систему координат, работающий на основе кватернионного умножения L*N*L, где L, N – кватернионы соответственно углов Эйлера и ускорений. На вход конвертора поступает вектор N = [nX, nY, nZ], на выходе получается вектор Ng = [nXg, nYg, nZg], необходимый для работы БИНС.
Математическая модель БСО, хотя и не включена в схему БИНС, является составной частью алгоритма БИНС, т.к. определение угловой ориентации подвижного объекта необходимо для решения задачи навигации.
Схема содержит следующие блоки:
1. Блок имитации параметров движения объекта, который осуществляет имитацию углового движения объекта с учетом изменения углов х, г, ш по синусоидальным законам и с учетом движения объекта вдоль Земли с линейной скоростью. Также этот блок осуществляет имитацию абсолютного ускорения объекта с учетом эволюции ускорений по осям географической системы координат по синусоидальным законам;
2. Блок основных датчиков (ДУС и акселерометры) выдает три составляющих абсолютной угловой скорости (щXS, щYS, щZS) и три компоненты кажущегося ускорения в связанной системе координат (nX, nY, nZ);
3. Блок дополнительных датчиков вычисляет данные об угловом движении объекта на основе избыточной информации (в данном случае с акселерометров и магнитометров);
4. Блок БСО, осуществляет решение кинематических уравнений углового движения объекта на основе информации, получаемой с ДУС и с дополнительных датчиков;
5. Блок БИНС осуществляет интегрирование скомпенсированных сигналов акселерометров и выдает координаты объекта в виде параметров ц, л, h;
Модель БИНС в среде Matlab Simulink представлена на рис. 2.2. На схеме в качестве основных датчиков представлены ДУС и акселерометры, играющие основную роль в работе БИНС, а также магнитометры, позволяющие реализовать комплексирование БСО.
В схеме имеется блок имитации исходных данных для задания углов ш, х, г и параметров ускорения объекта в земной системе координат (в данном случае по синусоидальным законам в разрешенных пределах). Задание других необходимых параметров для функционирования БСО и БИНС осуществляется в соответствующих блоках модели.
Схема модели БИНС содержит следующие блоки:
Блок Imitate имитирует угловое движение БПЛА с учетом изменения углов тангажа, крена и рыскания по синусоидальным законам и с учетом движения аппарата вдоль Земли с линейной скоростью. Кроме того, блок имитирует абсолютное ускорение аппарата по синусоидальному закону в географической системе координат.
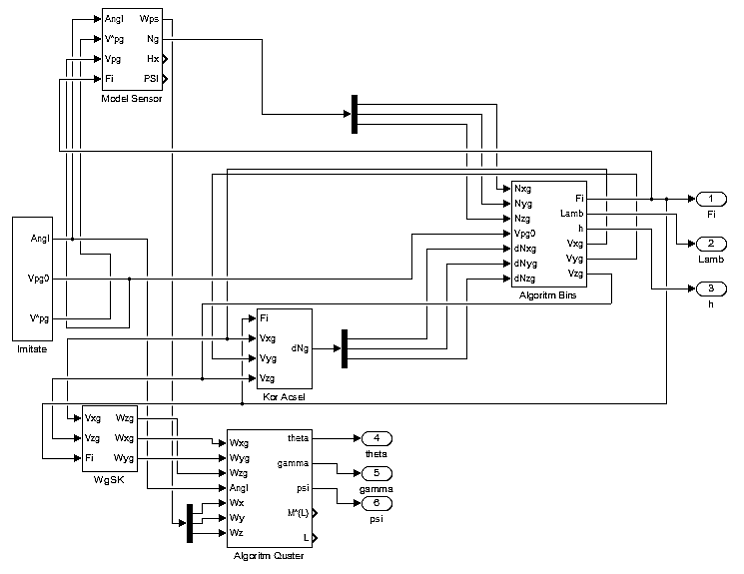
Рис. 2.2 Модель БИНС среде Matlab Simulink
Блок Model Sensor включает датчики измерительного модуля IMU (ДУС, акселерометр и магнитометр) и формирует три составляющие абсолютной угловой скорости (![]()
![]() , три компоненты кажущегося ускорения в связанной системе координат (
, три компоненты кажущегося ускорения в связанной системе координат (![]()
![]() , а также проекции вектора напряженности магнитного поля Земли (
, а также проекции вектора напряженности магнитного поля Земли (![]()
![]() на оси связанной системы координат.
на оси связанной системы координат.
Блок моделирования ускорений Acseleromete, входящий в состав блока Model Sensor работает на основе данных о составляющих ускорения объекта соответственно по осям географической системы координат, данных об угле широты места ц и значений ускорения свободного падения.
Сначала в блоке вырабатываются сигналы по известным формулам (2.7) [36]. Затем они пересчитываются в данные для выходов акселерометров – Nk с помощью матрицы направляющих косинусов Ao.
Выражение (2.7) содержит все составляющие кажущегося ускорения в земной системе координат: Ng=[nXg, nYg, nZg]. Далее, пересчитав компоненты nXg, nYg, nZg в связанную систему координат, получим компоненты кажущегося ускорения непосредственно с выходов датчиков – акселерометров (nX ,nY ,nZ ).
Блок Algoritm Quter системы ориентации, осуществляет решение кинематического уравнения Пуассона в кватернионах углового движения БПЛА на основе информации, получаемой с ДУС и дополнительных датчиков. Схема блока представлена на рис. 2.3.
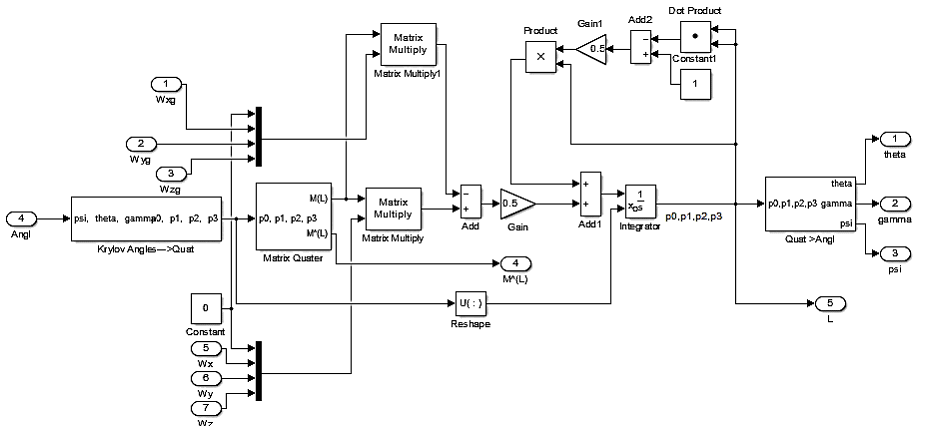
Рис. 2.3. Схема модели блока ориентации в кватернионах
Блок Algoritm Bins осуществляет интегрирование скомпенсированных сигналов акселерометров и выдает координаты объекта в виде параметров ц, л, h. В блок подается вектор кажущегося ускорения, полученный в результате компенсации ошибок в земной системе координат: Ng = [nXg, nYg, nZg], на выходе в результате интегрирования получается вектор координат C = [ц, л, h]. Схема блока представлена на рис. 2.4.
Блок Kor Acsel вычисляет ошибки акселерометров, связанные с кажущимся ускорением. Эти ошибки в виде поправки dNg компенсируются перед интегрированием сигналов ускорений – в итоге получаются истинные координаты объекта. Схема блока работает на основе формул (2.9).
Блок WgSK предназначен для получения данных в виде вектора Ng путем преобразования данных с акселерометров в земную систему координат.
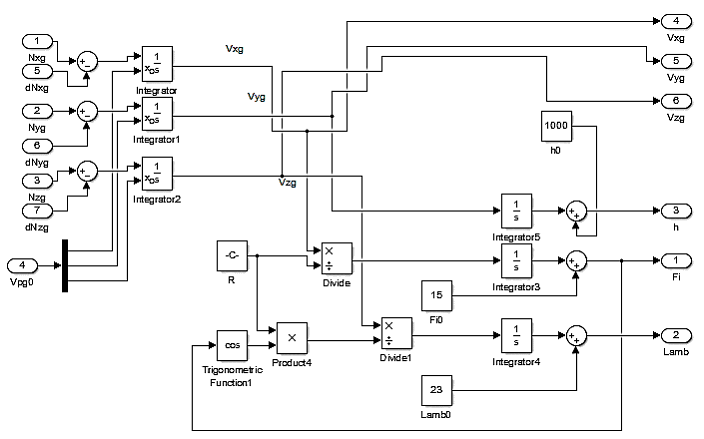
Рис. 2.4. Блок вычисления координат в земной системе координат
Моделирование проводилось для конкретного режима полета летательного аппарата. По угловому положению законы изменения углов синусоидальные: курса – амплитуда ![]()
![]() , частота 0,1 Гц; тангаж -
, частота 0,1 Гц; тангаж - ![]()
![]() , частота 0,15 Гц; крен -
, частота 0,15 Гц; крен - ![]()
![]() , частота 0,2 Гц. Время моделирования 100 с.
, частота 0,2 Гц. Время моделирования 100 с.
По ускорениям ЛА на основе синусоидальных законов в земной системе координат: по оси Xg: с амплитудой Vpxa = 4,5 м/с2; начальным значением Vpxb = 0 м/с2; частотой Vpxw = 0,3 Гц; по оси Yg: с амплитудой Vpya = 2,0 м/с2; начальным значением Vpyb = 0 м/с2; частотой Vpyw = 0,4 Гц; по оси Zg: с амплитудой Vpza = 3,0 м/с2; начальным значением Vpzb = 0 м/с2; частотой Vpzw = 0,2 Гц.
По скоростям в земной системе координат – начальные значения: Vxo = 300; Vyo = 0; Vzo = 150. По навигационным координатам – начальные значения: цo = 50 град; лo = 36 град; ho = 1000 м.
Проводилась симуляция заданного режима полета и совместной работы БСО и БИНС в течение 100 с. Задачей исследования эффективности БИНС является анализ точности оценивания координат подвижного объекта. С этой целью на основе информации об идеальных значениях скорости БПЛА, полученной в земной системе координат путем интегрирования истинных ускорений, предварительно вычисляются идеальные значения координат ЛА: ц, л, h.
Для моделирования показаний неортогонально расположенного блока в сигнал одного из модулей (гироскопа, а затем и акселерометра), вносились дополнительная составляющая (до 10% моделируемого сигнала) и шум в пределах паспортных данных модуля. Погрешности ориентации определялись относительно данных ортогонально расположенного измерительного модуля.
На первом этапе моделирования была использована модель исследования БИНС, представленная на рис. 2.5.
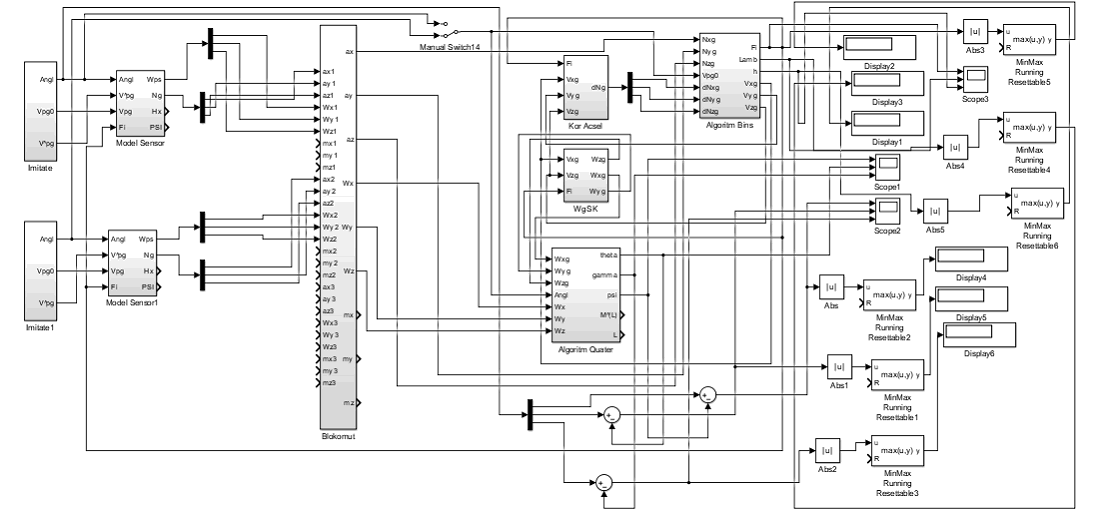
Рис. 2.5. Модель исследования БИНС с неортогонально расположенными блоками измерителей
На этом этапе исследовался алгоритм ориентации БИНС в параметрах Родрига-Гамильтона (в кватернионах) с целью его использования для решения задач рационального управления.
Погрешности ориентации по параметрам Родрига-Гамильтона проведен в составе БИНС. Ошибки не превышают 0.05 градуса при всех вариантах БСО.
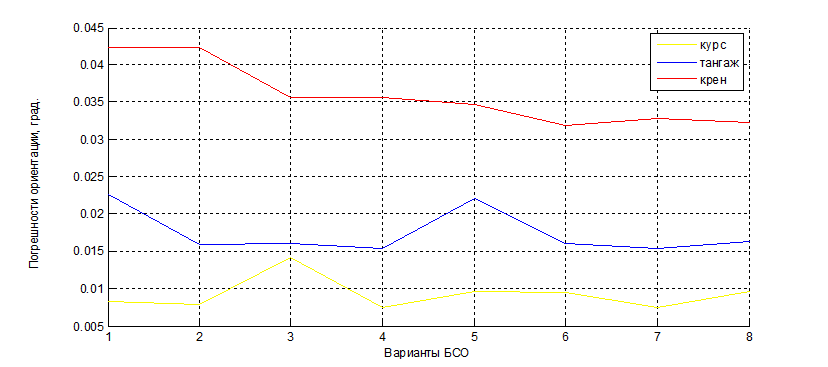
Рис. 2.6. Погрешности ориентации БИНС
На втором этапе моделирования исследовалось поведение БИНС при различных комбинациях измерителей. Определялись параметры ориентации и результаты решения навигационной задачи в случае выхода из строя гироскопа одного из модулей (на графиках обозначено 1) и акселерометра (на графиках обозначено 2). Результаты моделирования представлены на рис. 2.7 – 2.10.
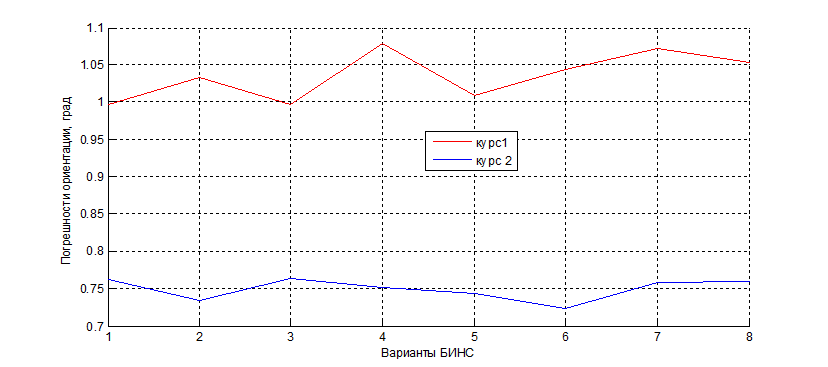
Рис. 2.7. Погрешности угла курса при различных вариантах БИНС:
1- неисправен гироскоп измерительного модуля; 2 – неисправен акселерометр модуля.
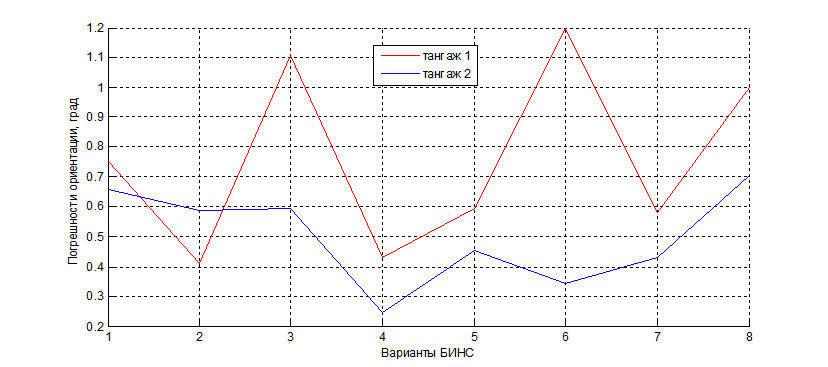
Рис. 2.8. Погрешности угла тангажа при различных вариантах БИНС:
1- неисправен гироскоп измерительного модуля; 2 – неисправен акселерометр модуля.
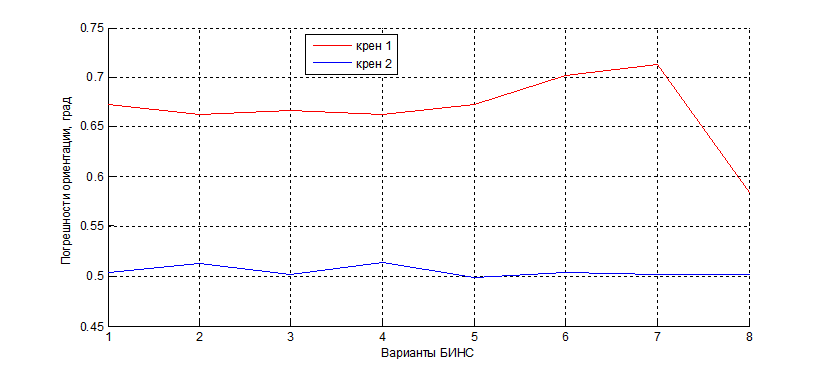
Рис. 2.9. Погрешности угла крена при различных вариантах БИНС:
1- неисправен гироскоп измерительного модуля; 2 – неисправен акселерометр модуля.
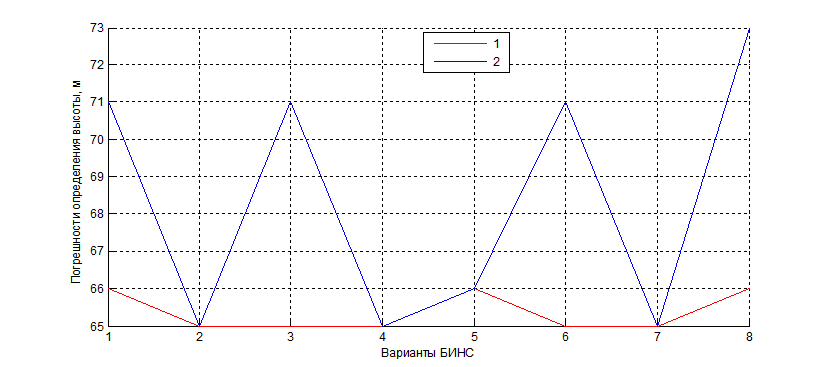
Рис. 2.10. Погрешности определения высоты полета при различных вариантах БИНС: 1- неисправен гироскоп измерительного модуля; 2 – неисправен акселерометр модуля.
Анализ полученных результатов показывает, что выход из строя гироскопа практически не влияет на решение навигационной задачи, а ошибки определения высоты находятся в пределах дhmax =7%. Выход из строя акселерометра приводит к ошибкам решения навигационной задачи: по широте Дϕmax= 14.5″ и Длmax= 11″, что соответствует погрешности определения широты в 448 м и долготы в 322 м. При этом погрешности ориентации значительно увеличиваются при всех вариантах комбинаций измерителей.
Библиографический список
- Ориентация и навигация подвижных объектов: современные информационные технологии. [Текст] /Под ред. Б.С. Алешина, К.К. Веремеенко, А.И. Черноморского. – М.: ФИЗМАТЛИЗ, 2006.- 424с.
- Управление и наведение беспилотных маневренных летательных аппаратов на основе современных информационных технологий /Под ред. М.Н. Красилыцикова и Г.Г. Себрякова. — М.: ФИЗМАТЛИТ, 2003. – 280с.
- Основы построения бесплатформенных инерциальных навигационных систем [Текст] /В.В. Матвеев, В.Я. Распопов /Под. общ. ред. д.т.н. В.Я. Распопова.- СПб.: ГНЦ РФ ОАО «Концерн ЦНИИ «Электроприбор», 2009.- 280с.
- Распопов В.Я. Микросистемная авионика: учебное пособие. [Текст] Тула: «Гриф и К», 2010. – 248с.
- Паршин А.П., Немшилов Ю.А. Разработка измерительного блока системы ориентации БПЛА с неортогональным расположением чувствительных элементов // Современная техника и технологии. 2016. № 3 [Электронный ресурс]. URL: http://technology.snauka.ru/2016/03/9697 (дата обращения: 09.03.2016).

Здравствуйте, не могли бы вы дать мне программу в матлабе? Занимаюсь разработкой БИНС