Введение
В теории информации энтропия является мерой неопределенности в отношении событий, связанных с сообщениями, которые могут иметь ту или иную вероятность [1]. Передача сообщений от источника к получателю осуществляется посредством сигналов. В то же время сигналы, как таковые, могут иметь случайный характер (например, сигнал белого шума) или соответствовать некоторому функциональному описанию (например, периодический сигнал). В первом случае они характеризуются полной неопределенностью, а во втором являются в некоторой степени предсказуемыми. С этой точки зрения ниже рассматривается способ оценки уровня неопределенности цифровых сигналов, для чего вводится парадигма нормы энтропии и анализируется поведение нормы энтропии цифровой обработке сигналов.
Определение нормы энтропии
Для характеристики независимых случайных событий с N возможными исходами в теории информации используется понятие энтропии [1]. Последняя определяется как количество информации, приходящейся на символ передаваемого сообщения, и выражается равенством:
H = – ![]() n logη pn (1)
n logη pn (1)
где:
pn - вероятность n-го состояния
η – основание логарифма
Заметим, что в равенстве (1) величина энтропии параметрически зависит от з. Эту зависимость, очевидно, можно исключить путем нормирования:
Ĥ = H/logη N (2)
В то же время для равновероятных событий pn = 1/N, и, таким образом:
![]() (3)
(3)
где Hmax - максимально возможное значение энтропии [1].
С учетом (2) окончательно получаем:
Ĥ = H/ Hmax (4)
где Ĥ будем называть нормой энтропии.
Норма энтропии цифрового сигнала
Цифровой сигнал представляет собой последовательность, каждый элемент которой принимает одно из значений в диапазоне изменения амплитуды сигнала [2]. Общее количество таких элементов определяется в виде:
N = A / δ (5)
где:
A - диапазон изменения амплитуды сигнала
δ - шаг квантования сигнала
Элементы такой последовательности можно рассматривать как независимые случайные события, для информационной оценки которых применима формула (1). Вероятности pn таких событий определяются частотой, с которой отдельные элементы встречаются в последовательности оцифрованных значений сигнала.
Наглядной аналогией нормы энтропии цифрового сигнала может служить игральная кость с N гранями, где «событием» является выпадение одной из граней с числом от 1 до N. При этом все события являются равновероятными, и норма энтропии равна единице или, эквивалентно, 100%.
Ниже приведены теоретические значения нормы энтропии для некоторых элементарных сигналов, рассматриваемых в теории цифровой обработки сигналов [2].
Таблица 1. Норма энтропии в случае элементарных сигналов.
| Элементарный сигнал |
Норма энтропии
|
| Сигнал постоянного уровня |
0
|
| Единичный сигнал |
0 < δ<<1
|
| Белый шум |
1
|
Заметим что, оценка нормы энтропии для любых других цифровых сигналов может быть определена только путем компьютерного моделирования.
Определение нормы энтропии белого шума
При компьютерном моделировании нормы энтропии в случае цифрового сигнала типа белого шума использовались генераторы псевдослучайных чисел (ПСЧ) с равномерным распределением [3]. Ниже на рис. 1 можно видеть, что значения нормы энтропии зависят от длины анализируемого фрагмента цифрового сигнала.
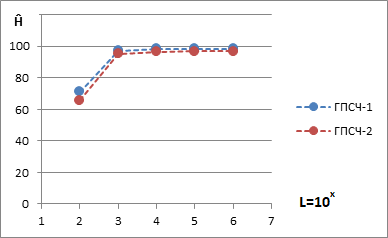
В то же время значения нормы энтропии могут различаться для двух неконгруэнтных генераторов псевдослучайных чисел – ГПСЧ-1 и ГПСЧ-2 (рис. 1). Тем не менее, в обоих случаях с увеличением длины фрагмента L оценка нормы энтропии приближается к теоретическому пределу, равному 100%.
Определение нормы энтропии сложного сигнала
Рассмотрим цифровой сигнал в виде суммы:
![]() (6)
(6)
где:
ak , bk , ck - амплитуда, частота и фаза k-й гармоники, соответственно
L - длина спектра
M - уровень сложности сигнала
В связи с этим представляет интерес зависимость нормы энтропии от уровня сложности сигнала. На рис. 2 представлены результаты определения нормы энтропии на базе достаточно длинной последовательности (6), причем S1 соответствует варианту с фиксированными амплитудами, а S2 – случайному выбору амплитуд в заданном диапазоне. Примечательно, что наименьшее значение нормы энтропии при этом достигается в случае моногармонического сигнала, т.е. при M = 1.
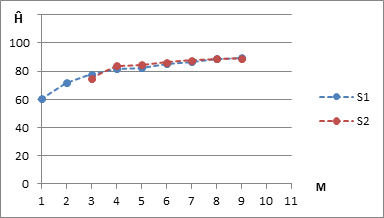
На рис. 2 хорошо видно, что по мере повышения уровня сложности сигнала, его норма энтропии увеличивается и стремится к некоторому значению, однако меньшему нормы энтропии для сигнала типа белого шума.
Шум квантования сигнала и норма энтропии
Одним из важных этапов аналого-цифрового преобразования является квантование сигнала [4]. При этом в результате округления до определённого разряда или отбрасывания младших разрядов возникает шум квантования. При корректном квантовании, ошибки квантования не коррелированы с сигналом и могут рассматриваться как аддитивный шум (рис. 3).
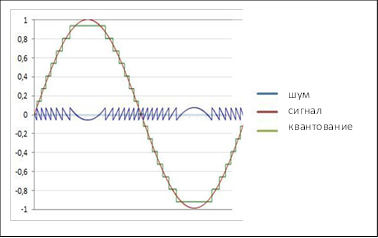
В то же время, шум квантования, очевидно, влияет на анализируемую величину нормы энтропии. Это подтверждается результатами компьютерного моделирования для моногармонического сигнала, изображенного на рис. 3.
Таблица 2. Влияние шума квантования на значение нормы энтропии.
| Количество уровней квантования (N) |
32
|
64
|
128
|
256
|
512
|
1024
|
16384
|
65536
|
| Норма энтропии (%) |
70
|
62
|
55
|
48
|
44
|
40
|
29
|
25
|
Заметим, что последнее значение нормы энтропии в Таблице 2 соответствует уровню шума 90 дБ, т.е. его практическому отсутствию. Таким образом, можно сделать вывод, что с увеличением количества уровней квантования сигнала вклад шумовой составляющей в норму энтропии цифрового гармонического сигнала уменьшается.
Влияние цифровой обработки сигналов на норму энтропии
Одним из наиболее часто встречающихся видов цифровой обработки сигналов является цифровая фильтрация. Рассмотрим класс цифровых фильтров с конечной импульсной характеристикой (КИХ). Передаточная функция КИХ фильтра в z-плоскости имеет вид [2]:
S(z) = ![]() (7)
(7)
где w(k) - импульсная характеристика КИХ фильтра.
При этом процесс фильтрации представляется дискретной линейной сверткой:
y(n) = ![]() (8)
(8)
где y(n) и x(n) являются элементами входной и выходной последовательностями цифрового сигнала.
Аналитическое определение нормы энтропии цифрового сигнала на выходе КИХ фильтра на основе равенств (7) и (8) не представляется возможным. Однако соответствующую оценку можно получить путем компьютерного моделирования. В качестве примера рассмотрим два КИХ фильтра нижних частот с коэффициентами вида:
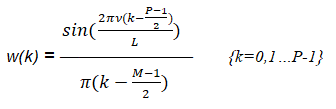 (8)
(8)
где:
P - порядок фильтра
ν - частота среза
Заметим, что выражение (8) определяет импульсную характеристику КИХ фильтра. В качестве примера, для компьютерного моделирования были выбраны два КИХ фильтра с импульсными характеристиками, изображенными на рис. 4.
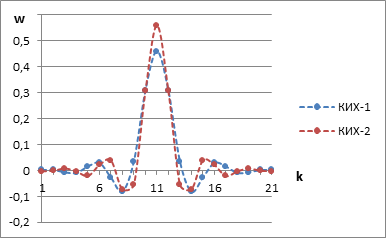
В Таблице 3 ниже представлены результаты компьютерного моделирования с КИХ и БИХ (см. ниже) фильтрами и входным сигналом типа белого шума, который генерировался с помощью стандартного генератора ПСЧ.
Таблица 3. Определение нормы энтропии (НЭ) при цифровой фильтрации белого шума.
|
Тип фильтра
|
Порядок фильтра
|
Частота среза
|
Длина последова-тельности
|
НЭ входного сигнала
|
НЭ выходного сигнала
|
|
КИХ
|
21
|
0.23
|
10 000
|
99%
|
89%
|
|
КИХ
|
21
|
0.28
|
10 000
|
99%
|
90%
|
|
БИХ
|
5
|
0.23
|
10 000
|
99%
|
92%
|
Из Таблицы 3 также следует, что значение нормы энтропии снижается по мере уменьшения частоты среза фильтра. Этот вывод качественно можно объяснить тем, что фильтр нижних частот подавляет верхнюю часть спектра белого шума в соответствии с частотой среза и, таким образом, уменьшает степень неопределенности сигнала.
Для оценки влияния цифровой фильтрации на норму энтропии сигнала можно использовать также фильтры с бесконечной импульсной характеристикой (БИХ), которые описываются дробно-рациональной функцией вида [2]:
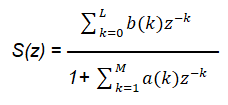 (9)
(9)
где M - порядок фильтра и L = M
Результаты компьютерного моделирования прохождения сигнала белого шума через эллиптический БИХ фильтр 5-го порядка представлены в Таблице 3 [5]. Коэффициенты передаточной функции этого фильтра в соответствии с выражением (9) (при L = M) приведены ниже в Таблице 4.
Таблица 4. Коэффициенты эллиптического фильтра 5-го порядка.
|
k
|
0
|
1
|
2
|
3
|
4
|
5
|
|
b(k)
|
0.01943
|
0.2111
|
0.03771
|
0.03771
|
0.02111
|
0.01943
|
|
a(k)
|
-
|
-2.7580
|
4.0110
|
-3.3711
|
1.6542
|
-0.3796
|
Обсуждение полученных результатов
В соответствии с данными компьютерного моделирования (рис. 1) оценка нормы энтропии для сигнала типа белого шума, моделируемого генератором ПСЧ, по мере увеличения длины последовательности стремится к некоторому предельному значению, равному 100%. Очевидно, что чем ближе эта оценка к 100%, тем в большей степени ПСЧ соответствует идеальной случайной последовательности. С этой точки зрения, норма энтропии может быть использована для качественной оценки генераторов ПСЧ в моделях методов Монте-Карло [6]. Кроме того, парадигма нормы энтропии применима к любой совокупности данных, таких как фондовые или демографические индексы. При этом может быть определено, в какой степени эти данные можно считать случайными. Обобщая полученные результаты, можно утверждать, что прохождение сигнала через любую линейную систему с передаточными функциями вида (7) или (9) приводит к снижению нормы энтропии сигнала, и, следовательно, к уменьшению степени неопределенности сигнала.
Выводы
Рассмотрен способ оценки степени неопределенности цифровых сигналов с использованием парадигмы нормы энтропии сигнала. Показано, что норма энтропии цифровых сигналов изменяется в пределах от нуля, в случае постоянного сигнала, до единицы, в случае белого шума. В качестве приложения, норма энтропии может быть использована для оценки качества генераторов ПСЧ в моделях методов Монте-Карло или для оценки любой совокупности данных, таких как фондовые индексы или сигналы неизвестного происхождения. Показано, что при прохождении сигнала через любую цифровую систему с передаточной функцией в z-плоскости норма энтропии цифрового сигнала уменьшается.
Библиографический список
- Шеннон К. Работы по теории информации и кибернетике. – М.: Изд. иностр. лит., 1963: 830 с.
- Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. – М.: Мир, 1978: 848 с.
- James E. Gentle. Random Number Generation and Monte Carlo Methods. – Springer Science & Business Media. 2013: 247 p.
- Виды искажений сигнала при оцифровке и способы их минимизации [Электронный ресурс]. URL: http://www.digitalmusicacademy.ru/lesson-distortion-types
- IIR Filters. [Электронный ресурс]. URL: http://www.eas.uccs.edu/~mwickert/ece2610/lecture_notes/ece2610_chap8.pdf
- Сучилин В.А. π-Test and Monte Carlo Optimization of Pseudo-Random Sequence Generators // Современные научные исследования и инновации. 2018. № 8 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2018/08/87545.
