Решать позиционные задачи приходится на всех стадиях проектирования изделия. Основную сложность при построении чертежа представляет построение пересекающих поверхностей. Существует несколько различных способов определения общих элементов геометрических фигур. Выбор способа построения происходит в зависимости от формы пересекающихся поверхностей и их взаимного положения. Если одна из фигур занимает проецирующее положение, следовательно, линия пересечения будет совпадать с вырожденной проекцией на одну из плоскостей проекций. Способ секущих плоскостей используется, если обе поверхности общего положения. Если пересекаются поверхности вращения, в качестве секущей поверхности используют сферу. Самым универсальным из способов является способ секущих плоскостей посредников, который можно использовать в любом случае. Данный способ применим в различных способах проецирования: центральном, параллельном, прямоугольном. При этом геометрические построения несколько отличаются друг от друга, но алгоритм решения один. Рассмотрим несколько примеров.
Для определения принадлежности точки заданной поверхности используется одна вспомогательная горизонтальная плоскость. Эта плоскость проводится через заданную точку и рассекает поверхность. Точка принадлежит поверхности, если лежит на линии сечения.
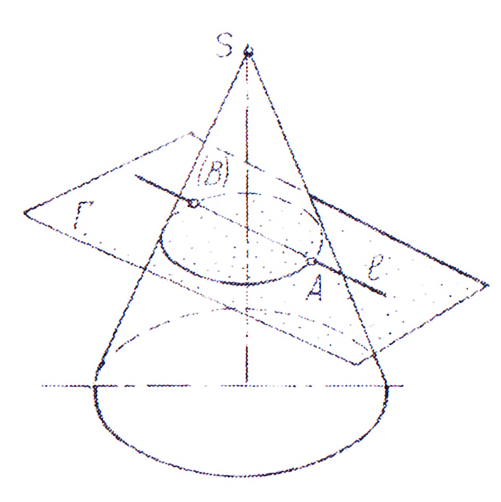
Точка пересечения прямой линии с поверхностью или плоскостью определяется по алгоритму первой позиционной задачи. На рисунке 1 представлен пример определения точек пересечения прямой с конусом. Заданная прямая l заключается в плоскость Г. Затем, строится линия пересечения плоскости и заданной поверхности конуса. Искомые точки А и В расположены в пересечении заданной прямой и линии пересечения. В данном алгоритме используется одна вспомогательная плоскость.
Рисунок 1. Пересечение прямой линии с конической поверхностью
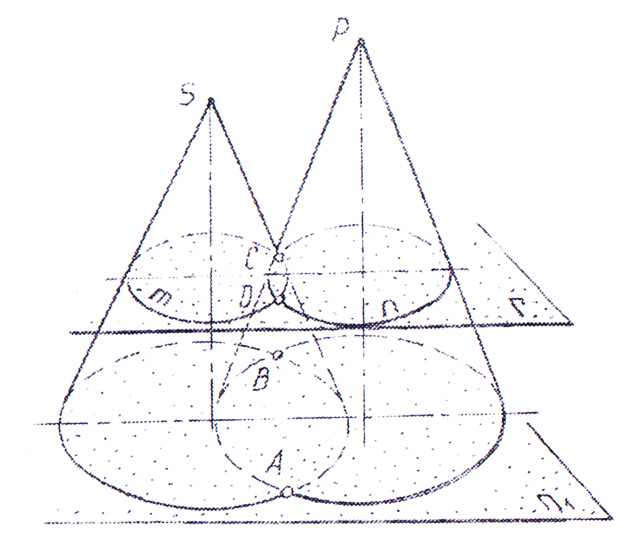
Для определения линии пересечения двух поверхностей, используют несколько секущих плоскостей. На рисунке 2 линия пересечения двух конических поверхностей строится с использованием нескольких горизонтальных плоскостей Г, П т.д. Полученные в сечении окружности m, n пересекаются в точках D и С, принадлежащих линии пересечения. Соединив полученные точки, получим искомую линию пересечения.
Рисунок 2. Пересечение двух конических поверхностей
Для построения линии пересечения наклонных конических поверхностей на рисунке 3 используют плоскости общего положения, проходящие через прямую m, соединяющую вершины заданных конусов и прямые l образующие конус. Эти плоскости рассекают оба конуса по прямолинейным образующим. В пересечении образующих заданных конусов получаем искомые точки А, В, С, принадлежащие линии пересечения.
Рисунок 3. Пересечение наклонных конических поверхностей
В каждой из представленных задач используются вспомогательные секущие плоскости. Такие плоскости пересекают данные поверхности по графически простым линиям: прямым или окружностям. Точки пересечения полученных линий являются точками искомой линии пересечения. Этот алгоритм является общим для решения позиционных задач в любых проекциях. Его применение существенно упрощает решение и не требует пространственного представления задачи.
Библиографический список
- Инженерная графика. Пересечение поверхностей: методические указания к выполнению эпюра № 4 / Юго-Зап. гос. ун-т; сост.: Ж.С. Калинина, С.И. Иванова, Ю.В. Скрипкина Курск, 2013. 39 с.: ил. 17. Библиогр.: с. 39.
- Красильникова Г.А. Начертательная геометрия и инженерная графика. Краткий курс лекций по начертательной геометрии: учебное пособие / Г.А.Красильникова, М.С.Кокорин, Н.С.Иванова. — СПб. : Изд-во Политехн. ун-та , 2015.
- Наумова Ж. Л. Начертательная геометрия: Учебное пособие для самостоятельной работы. – Хабаровск: Изд-во Хабар. гос. техн. ун-та, 2003. – 68 c.
- Горельская Л.В. начертательная геометрия. Учебное пособие по курсу «Начертательная геометрия» / Л.В. Горельская, А.В. Кострюбков, С.И. Павлов – Оренбургский государственный университет. - Оренбург, 2000 – 118с., с ил.