Introduction
To date, a pseudo-random number generator (PRNG) is considered indispensable for any modern software package [1]. However, the standard software functions in use generating pseudo-random numbers (PRN) differs among themselves in regard to the quality that may exercise unpredictable effects on the results of statistical calculations [2]. From this point of view, the quality of a PRNG plays an important role [3]. In this article, for the purpose of evaluation of PRNG quality, a new two-stage PRNG test procedure is presented, the core of which is the Inverse Box-Muller Transform (BMT) [4]. Below the Direct BMT is described and on the basis of this description the Inverse BMT is formulated.
Direct Box-Muller Transform
For the transition from the Gaussian type PRN to the PRN with the uniform distribution mainly use the well-known Direct BMT, that can be presented as follows [4]:
u = ![]() (1)
(1)
v = ![]()
where
x и y – two statistically independent random variable distributed uniformly on
interval (0,1)
u и v – two statistically independent random variable distributed normally with
average and variance equal to 0 and 1 accordinglyThe standard use of the Direct BMT in the form (1) allows obtaining PRNG with a normal distribution on the basis of an eventually ideal PRNG with the uniform distribution.
As a matter of fact, the PRNGs used in software do not provide the perfect uniform distribution. That is due to the methods of PRN generating and limitations of the decimal places of the variable used by calculations in the course of statistical calculations.
Inverse Box-Muller Transform
Opposing to the formulation given above, an approach may be considered where conversion of the PRN with the normal distribution leads to the adequate PRN with the uniform distribution. As will be shown below, due to such inverse transform, a quality check of the Gaussian type PRNG can be reduced to the evaluation of the quality of the PRNG with the uniform distribution.
The Inverse BMT can be derived immediately from the expression (1). To do this, at first one should divide the second entity in (1) by the first one, as a result of which we obtain:
v/u = ![]() (2)
(2)
On the other hand, after squaring and subsequent addition of the both entity in (1), follows:
u2+v2 = - 2 ln y (3)
Finally, on the basis of equalities (2) and (3), the Inverse BMT can be formulated as follows:
x =![]() / 2р (4)
/ 2р (4)
y = e-s
where
p = v/u
s = (u2+v2)/2
u и v – two statistically independent random variable distributed normally with average and variance equal to 0 and 1 accordinglyx и y – two statistically independent random variable distributed uniformly oninterval (0,1)Inverse BMT is unique, and its superposition with Direct BMT leads to an identity. The formal proving of this statement is beyond the scope of this article, but its validity was confirmed through computer simulation with the modules shown in the following tables. Below, there is also the original function GetNormRandNumber (not given here) that allows obtaining the Gaussian type PRN.
Table 1. Program “Superposition of Direct & Inverse BMT”
| ‘Main programmtextwindow.Write(” Box-Muller Transform Example “)
textwindow.Read() textwindow.Write(“——————————————-”) textwindow.Read() textwindow.Write(” Initial Random number “) textwindow.Write(“Direct Transform “) textwindow.Write(“Inverse Transform “) textwindow.Read() textwindow.Write(“——————————————-”) textwindow.Read() For i=1To N_Sample ‘Direct Transform DirBoxMuller() ‘Invers Transform InvBoxMuller() textwindow.Write(“”+x1) textwindow.Write(” “+u) textwindow.Write(” “+x2) textwindow.Read() textwindow.Write(“”+y1) textwindow.Write(” “+v) textwindow.Write(” “+y2) textwindow.Read() EndFor ‘End of programm |
Table 2. Module “Direct BMT”
| Sub DirBoxMuller x1=Math.GetRandomNumber(z)/z
y1=Math.GetRandomNumber(z)/z u=Math.Cos(2*Math.pi*x)*Math.SquareRoot(-2*Math.NaturalLog(y)) v=Math.Sin(2*Math.pi*x)*Math.SquareRoot(-2*Math.NaturalLog(y)) EndSub |
Table 3. Module “Inverse BMT”
| Sub InvBoxMuller GetNormRandNumber()
u=NormValue GetNormRandNumber() v=NormValue x2=Math.ArcTan(v/u)/(2*Math.pi) y2=Math.Power(exp,-(u*u +v*v/2) EndSub |
Table 4. The screenshot “Superposition of Direct & Inverse Box-Muller”.
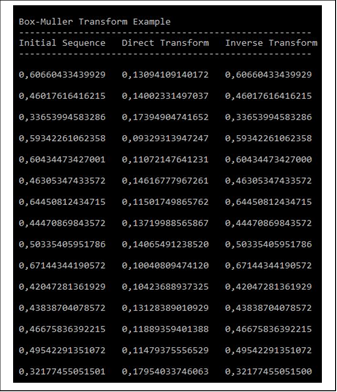
In the screenshot above, it is easy to see that the consistent use of the Direct and Inverse BMTs leads to the initial PRN. Thus, it shows that the superposition of the both transforms is unique and leads to identity.
Application of the Inverse Box-Muller Transform
In regard to the representation above, the procedure for the quality evaluation of PRNG can be implemented in the form of a two-stage procedure in which the PRN with the uniform distribution will be formed by means of Inverse BMT, and then the π-Test is applied [5].
Generally, to check the effectiveness of the described approach the Central Limit Theorem Probability can be used [6]. According to this theorem, a PRN which elements defined as the average of the original set of statistically independent random variable has the Gaussian distribution. The program generating the Gaussian type PRN on the basis of the N-set mentioned above is presented below.
Table 5. Module “Gaussian type PRNG”
| Sub GetNormRandNumber Smp=0
For si=1To N RndLCM() Smp=Smp+RandValue EndFor NormValue=Smp/N EndSub |
Note, a special function RndLCM is applied above, namely one on the basis of Linear Congruential Method (LCM), which provides a smart PRN with statistically independent variable [5]. The distribution density curves calculated in such way for some values N are represented below.
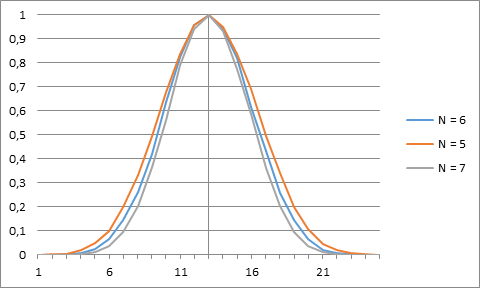
Fig. 1 Distribution density diagrams for sampled values N on the basis of the Central Limit Theorem Probability.
The diagram below shows results of computer simulation of the proposed two-stage test procedure to the quality evaluation of the Gaussian type PRNG by N = 6 vs. results for two other (reference) PRNGs with uniform distribution.
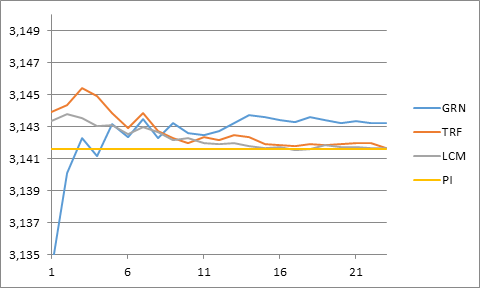
Fig. 2 PRNGs quality diagram.
The curves in the Fig. 2 represent the dynamics of the 23 sequential test sessions.
The legend of the Fig. 2 is as follows:
GRN – immediate π-Test of the PRNG with the use of function GetRandomNumber
TRF – two-stage procedure with the use of Central Limit Theorem Probability on the
first step and Inverse BMT on the second
LCM – immediate π-Test of the PRNG based on the Linear Congruential Method
PI – the value of π ( 3.14159…)
Discussion
The blue curve
in the Fig. 2 corresponds to the π-Test by the standard function GetRandomNumber with uniform distribution [7], while the second diagram (red curve) was calculated by means of the two-stage procedure described above. It should be emphasized that hereby a comparatively “simple” generator on the basis of the Central Limit Theorem Probability was applied. At the same time, it is easy to see that the use of GetRandomNumber leads to the worst indices.
It is all the more remarkable that in this case the two-stage testing procedure using Inverse BMT has a fairly smart match with the “LCM”
curve that is meanwhile the best of all and practically provide the approximation of the number π with the same accuracy. However, this of course does not preclude the use of the standard statistical testing methods for quality check of PRNGs and can be a good complement to them.
Conclusion
The Inverse Box-Muller transform was considered, which allows the transition from Gaussian type PRN to the adequate PRN with uniform distribution. A procedure for testing a Gaussian type PRNG is proposed by which after applying of the described Inverse BMT the quality of the PRNG with the uniform distribution (by means of π-Test) can be evaluated. The results of computer simulations confirm the effectiveness of the proposed approach. In addition, the described testing procedure is suitable for the testing of PRNGs of any type, since it uses just a random sequence with statistically independent variable. But the latter can belong to any PRNG and thus can be reduced to the Gaussian type sequence on the basis of the Central Limit Theorem Probability.
References
- Intel Digital Random Number Generator (DRNG): Software Implementation Guide. [Электронный ресурс] https://software.intel.com/en-us/articles/intel-digital-random-number-generator-drng-software-implementation-guide
- Stephen K. Park and Keith W. Miller (1988). Random Number Generators: Good Ones Are Hard To Find. Communications of the ACM 31 (10): 1192 – 1201[4]
- James E. Gentle. Random Number Generation and Monte Carlo Methods. Springer Science & Business Media, 2013: 247 с.
- Glasserman Paul. Monte Carlo Methods in Financial Engineering. Springer Science & Business Media, 2004 – 596 S.
- Сучилин В.А. π-Test and Monte Carlo Optimization of Pseudo-Random Sequence Generators // Современные научные исследования и инновации. 2018. № 8 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2018/08/87545 (дата обращения: 25.09.2018)
- Dudley M. Richard. Uniform Central Limit Theorems. Cambridge University Press, 1999 – 436 p.
- Small Basic – The Programmer’s Guide. [Электронный ресурс]. https://www.i-programmer.info/programming/other-languages/5196-small-basic-the-programmers-guide.html
