Физическая среда передачи данных, не являясь абсолютно надёжной, способствует появлению одиночных или групповых ошибок передачи информации. В результате воздействия помех биты передаваемой информации могут как исчезать, так и появляться лишние. Криптографические методы защиты информации от несанкционированного доступа к ней при передаче по каналам связи чувствительны к таким искажениям. В зависимости от режимов использования алгоритмов шифрования изменение одного бита зашифрованных данных (криптограмм) может привести к их полной потере, что в свою очередь увеличивает количество повторных передач и уменьшает пропускную способность защищенного канала связи. Вследствие чего возникает потребность в использовании систем, которые были бы устойчивы к воздействию таких искажений. При этом возникают проблемы, связанные с согласованием методов, обеспечивающих защиту от искажений c применяемой криптосистемой. Некорректная работа или возникновение сбоя в системе защиты от ошибок может привести к тому, что она не обнаружит (не исправит) ошибку или выдаст отказ в обработке принимаемых данных [1, с. 1375].
Для достоверной передачи криптограмм в основном применяются помехоустойчивые коды. Проведя анализ существующих криптосистем с помехоустойчивым кодированием, можно выделить следующие:
– криптосистема Мак Элиса;
– криптосистема Нидеррайтера;
– криптосистема на основе R-кодов;
– помехоустойчивая модулярная криптосистема.
Наиболее известной криптосистемой с открытым ключом на основе теории алгебраического кодирования является криптосистема Мак Элиса на основе класса кодов, исправляющих ошибки, называемых кодами Гоппа (Goppa). Основная идея данной криптосистемы заключается в том, чтобы создать код Гоппа и замаскировать его под обычный линейный код [2, c. 13].
Существует быстрый алгоритм декодирования кодов Гоппа, но общая проблема нахождения слов кода по данному весу в линейном двоичном коде является NP-полной задачей. Анализ криптостойкости данного алгоритма показывает, что для надежной защиты информации требуется учитывать минимальные значения параметров матрицы n = 1024 и k = 524 (где n – число строк, k – число столбцов). Помехоустойчивость алгоритма напрямую зависят от параметра t (количество ошибок, которое можно исправить), значение которого необходимо выбирать из условия![]() . Данная оценка является оптимальной для каналов связи с вероятностью появления ошибки
. Данная оценка является оптимальной для каналов связи с вероятностью появления ошибки![]() . Для надежной криптографической защиты необходимо получить такую сложность декодирования, которая соответствовала бы современным криптографическим требованиям (
. Для надежной криптографической защиты необходимо получить такую сложность декодирования, которая соответствовала бы современным криптографическим требованиям (![]() ). Данная сложность в рассматриваемой криптосистеме обеспечивается за счет большого количества используемых столбцов проверочной матрицы кода Гоппа (порядка 800).
). Данная сложность в рассматриваемой криптосистеме обеспечивается за счет большого количества используемых столбцов проверочной матрицы кода Гоппа (порядка 800).
При выполнении необходимых граничных требований к параметрам криптосистемы Мак Элиса обеспечивается достаточно надежная криптографическая защита информации, подтверждаемая целым рядом известных попыток ее неуспешного криптоанализа. Однако открытый ключ криптосистемы Мак Элиса имеет огромный по современным меркам размер (порядка ![]() бит).
бит).
Криптосистема Нидеррайтера строится на основе обобщенного кода Рида-Соломона [3, c. 124]. Сообщение в данном случае представляется в виде векторов с координатами из поля GF(q) и весом, не превосходящим ![]() (где q – число элементов поля Галуа; r – порядок матрицы S). При этом сообщения не являются кодовыми словами выбранного кода Рида-Соломона, а представляют собой всевозможные ошибки, которые этот код в состоянии исправить.
(где q – число элементов поля Галуа; r – порядок матрицы S). При этом сообщения не являются кодовыми словами выбранного кода Рида-Соломона, а представляют собой всевозможные ошибки, которые этот код в состоянии исправить.
Закрытый ключ криптосистемы Нидеррайтера является:
1) проверочной матрицы некоторого обобщенного кода Рида-Соломона над GF(q);
2) невырожденной матрицы S порядка r над GF(q), выбранной случайно с целью сокрытия от криптоаналитика существующих закономерностей.
Открытым ключом также является матрица. Размер открытого ключа в криптосистеме Нидеррайтера в ![]() раз меньше, чем в системе Мак Элиса.
раз меньше, чем в системе Мак Элиса.
Зашифрованный текст, соответствующий открытому тексту M, вычисляется по определенному правилу. При расшифровании получатель умножает его на обратную матрицу![]() , после чего применяет известный лишь ему алгоритм быстрого декодирования и получает открытый текст.
, после чего применяет известный лишь ему алгоритм быстрого декодирования и получает открытый текст.
В отличие от криптографической системы Мак Элиса в криптосистеме Нидеррайтера не используются случайные параметры, в результате чего зашифрование одинаковых исходных сообщений приводит к формированию одинаковых криптограмм.
В криптосистеме Нидеррайтера по сравнению с криптосистемой RSA скорость зашифрования выше приблизительно в 50 раз, а расшифрования – в 100 раз. Однако для шифрования произвольного сообщения необходим алгоритм перевода в q-арный вектор длиной n с весом не более t.
Для повышения помехоустойчивости криптосистемы также возможно применение R-кодов. Минимальное расстояние Хэмминга ![]() R-кодов уступает большинству известных помехоустойчивых кодовых конструкций, однако они обладают дополнительными криптографическими свойствами, которые позволяют организовать систему защиты информации с коррекцией ошибок только на приемной стороне, обладающей общим секретом (ключом).
R-кодов уступает большинству известных помехоустойчивых кодовых конструкций, однако они обладают дополнительными криптографическими свойствами, которые позволяют организовать систему защиты информации с коррекцией ошибок только на приемной стороне, обладающей общим секретом (ключом).
Известно, что кратность исправляемых помехоустойчивым кодом ошибок ![]() . Одним из вариантов использования R-кодов является система с каналом без помех, в которой случайные ошибки кратностью не выше t вносятся передающей стороной [4, c. 107]. В данном случае криптоаналитик, решая обратную криптографическую задачу, вынужден учитывать возможные варианты случайной ошибки. В случае атаки переборными методами по всему множеству двоичного ключевого пространства количество вариантов увеличивается на величину
. Одним из вариантов использования R-кодов является система с каналом без помех, в которой случайные ошибки кратностью не выше t вносятся передающей стороной [4, c. 107]. В данном случае криптоаналитик, решая обратную криптографическую задачу, вынужден учитывать возможные варианты случайной ошибки. В случае атаки переборными методами по всему множеству двоичного ключевого пространства количество вариантов увеличивается на величину![]() . Более того, без знания ключа криптоаналитик не располагает информацией о минимальном расстоянии используемого кода и вынужден вести атаку по наилучшему представителю R-кода с заданными параметрами (n, k).
. Более того, без знания ключа криптоаналитик не располагает информацией о минимальном расстоянии используемого кода и вынужден вести атаку по наилучшему представителю R-кода с заданными параметрами (n, k).
Также возможны комбинированные варианты криптосистем на основе R-кодов со случайными преднамеренными и непреднамеренными ошибками в канале передачи информации. В этом случае декодер в основном строится по принципу максимального правдоподобия с последующим расшифрованием кодового слова.
Помехоустойчивая модулярная криптосистема основывается на китайской теореме об остатках.
В модулярном коде любое число ![]() , где
, где ![]() однозначно представляется последовательностью вычетов
однозначно представляется последовательностью вычетов ![]() , так что
, так что ![]() ;
; ![]() , а
, а ![]() – попарно простые числа, являющиеся основаниями системы.
– попарно простые числа, являющиеся основаниями системы.
На основании китайской теоремы об остатках система вычетов
.gif)
имеет единственное решение, если выполнены вышеуказанные условия.
Целое неотрицательное число ![]() , где
, где ![]() , представленное вычетами
, представленное вычетами ![]() по системе попарно простых модулей
по системе попарно простых модулей![]() может быть однозначно восстановлено посредством рекурсии:
может быть однозначно восстановлено посредством рекурсии:
.gif)
где
Открытый текст М произвольной длины разбивается на n блоков ![]() определенной длины. Соответственно, для получения последовательности криптограмм
определенной длины. Соответственно, для получения последовательности криптограмм ![]() потребуется n операций зашифрования.
потребуется n операций зашифрования.
.gif)
где E – функция зашифрования;
![]() – ключи зашифрования (расшифрования).
– ключи зашифрования (расшифрования).
При передаче последовательности криптограмм ![]() влияние искажений проявляется в том, что вместо переданных принимаются другие криптограммы
влияние искажений проявляется в том, что вместо переданных принимаются другие криптограммы ![]() . Таким образом, адресат получит открытые тексты
. Таким образом, адресат получит открытые тексты ![]() отличающиеся от исходных
отличающиеся от исходных ![]() [5–6].
[5–6].
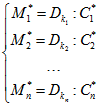
где D – функция расшифрования.
Для зашифрования и расшифрования может использоваться как один ключ, так и n ключей, соответствующих количеству блоков открытого текста. Кроме того, важным моментом является возможность передачи блоков открытого текста ![]() , образованных как из сообщения, принадлежащего одному пользователю, так и из независимых сообщений, принадлежащих n пользователям.
, образованных как из сообщения, принадлежащего одному пользователю, так и из независимых сообщений, принадлежащих n пользователям.
В помехоустойчивой модулярной криптосистеме в целях повышения достоверности передаваемой информации в условиях воздействия помех и атак злоумышленника на зашифрованный канал связи выполняется операция расширения модулярного кода путем введения избыточных оснований ![]() , удовлетворяющих условию
, удовлетворяющих условию ![]() , и получения избыточных вычетов
, и получения избыточных вычетов ![]() .
.
Для восстановления криптограммы ![]() по
по ![]() не обязательно знание значений всех остатков
не обязательно знание значений всех остатков ![]() , где
, где ![]() , а достаточно знания любых остатков
, а достаточно знания любых остатков ![]() , где
, где ![]() .
.
Таким образом, представления криптограмм в расширенном модулярном коде ![]() имеют r избыточных остатков, которые можно использовать для обнаружения и исправления ошибок в целях повышения достоверности передачи информации. Расширенный модулярный код позволяет обнаружить все одиночные ошибки уже при r = 1, а исправить при r = 2. Под q-кратной ошибкой будем понимать произвольное искажение q блоков
имеют r избыточных остатков, которые можно использовать для обнаружения и исправления ошибок в целях повышения достоверности передачи информации. Расширенный модулярный код позволяет обнаружить все одиночные ошибки уже при r = 1, а исправить при r = 2. Под q-кратной ошибкой будем понимать произвольное искажение q блоков ![]() . Следовательно, в случае искажения не более r – 1 переданных блоков криптограммы на приемной стороне можно полностью восстановить все переданное сообщение.
. Следовательно, в случае искажения не более r – 1 переданных блоков криптограммы на приемной стороне можно полностью восстановить все переданное сообщение.
Основным недостатком криптосистем с помехоустойчивым кодированием с точки зрений криптографической стойкости является искусственная информационная избыточность, вносимая алгоритмами кодирования для обнаружения и исправления ошибок, что приводит к существенному увеличению закрытого текста по отношению к исходному. Кроме того, размер ключей криптосистем с помехоустойчивым кодированием гораздо больше, чем в классических криптосистемах с открытым ключом, что существенно сказывается на их производительности [7, c. 394].
Однако, метод объединения процедур кодирования и шифрования для защиты данных от воздействия искажений различного происхождения является более эффективным с точки зрения повышения достоверности передачи данных по сравнению с традиционным (раздельным) использованием помехо- и криптозащиты, в которых шифрование и кодирование выполняются независимо, с использованием разных алгоритмических методов.
В качестве актуального направления дальнейших исследований можно выделить исследование возможности применения криптографических систем, основанных на помехоустойчивом кодировании с естественной избыточностью. Перспектива появления квантовых компьютеров так же дает предпосылки к исследованию возможностей ускорения алгоритмов с целью противостояния более эффективным атакам.
Библиографический список
- Godoy W., Periera D. A proposal of a cryptography algorithm with techniques of error correction // Computer Communications. – 1997. – № 20 (15). – С. 1374-1380.
- Бородин М. А., Чижов И. В. Эффективная атака на криптосистему Мак-Элиса, построенную на основе кодов Рида – Маллера // Дискретная математика. 2014. Т. 26. № 1. С. 10–20.
- Самохина М.А. Модификации криптосистемы Нидеррайтера, их стойкость и практические применения // Тр. МФТИ. – М., 2009. – Т. 1, № 2.– С. 121-127.
- Д.М. Бильдюк, С.Б. Саломатин. Дистанционные свойства нелинейного помехоустойчивого кода на базе криптографического алгоритма rijndael // Белорусский государственный университет информатики и радиоэлектроники – Минск – 2014. – с. 106-110
- Финько О.А. Групповой контроль ассиметричных криптосистем методами модулярной арифметики // Материалы XIV Международной школы-семинара «Синтез и сложность управляющих систем» / Нижегород. пед. ун-т. – Н. Новгород, 2003. – С. 85-86.
- Финько О.А. Многоканальные модулярные системы, устойчивые к искажениям криптограмм // Материалы Международной научной конференции «50 лет модулярной арифметике». – М.: «Ангстрем», МИЭТ, 2006. – С. 552–558.
- Блейхут Р. Теория и практика кодов, контролирующих ошибки / Р. Блейхут. – М. : Мир, 1986. – 576 с.
