СПОСОБЫ ПРЕДРАСЧЕТА ТОЧНОСТИ МАРКШЕЙДЕРСКИХ СЪЕМОЧНЫХ ПОСТРОЕНИЙ

Результатом всех маркшейдерско-геодезических работ является получение искомого значения той или иной величины. Вне зависимости от рода проведенных измерений, все они несут в себе погрешность, которую следует выявлять и в максимально возможной мере исключать для получения достаточно точного значения определяемой величины. В случае проектировании линейно-угловых сетей инструкция [1] регламентирует величину средней квадратической погрешности положения любого из пунктов хода. Оценка точности хода производится на основании формулы переноса погрешностей, позволяющей определить ошибку величины, являющейся функцией нескольких переменных [2]:

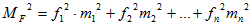,      (1)

где f_i – частная производная функции по измеряемому параметру, m_i – среднеквадратическая погрешность измерения параметра.

При проложении висячего хода с одной гиростороной (пример представлен на рис. 1) инструкция по производству маркшейдерских работ [1] требует прокладывать ход дважды. 

В этом случае погрешность положения последней точки, с учетом влияния погрешности определения дирекционного угла исходной стороны, а также погрешностей угловых и линейных измерений, при проложении хода с использованием электронного тахеометра, будет определяться по формуле:

,      (2)

где m_β – СКП угловых измерений; m_α – СКП определения дирекционного угла гиростороны; L – длина отрезка, соединяющего первую и последнюю точки хода; R – длины отрезков, соединяющих последнюю и i-ую точки хода; α – дирекционный угол стороны; a, b – паспортные коэффициенты погрешности измерений светодальномером. 

Для предрасчета погрешности положения последней точки хода необходимо выполнить ряд построений в САПР, снять с плана построения все необходимые данные и просчитать погрешность положения наиболее «слабой» точки (в данном случае – наиболее удаленной от исходной стороны). Формально задача оценки точности проектируемого хода будет выполнена (сравнение с допуском из инструкции [1]), но оценить негативные факторы, влияющие на точность определения положения точки n, выявить оптимальный способ повышения точности построения, оптимальную геометрию хода, будет затруднительно. 

Существует возможность выполнить подобную оценку в среде программного комплекса «Credo_DAT»: для этого необходимо будет указать координаты всех точек хода, планируемые измерения и предполагаемые величины СКП измерений. В настройках процедуры уравнивания следует выбрать функцию «Проект». В этом случае программа самостоятельно генерирует ожидаемые ошибки и производит процедуру уравнивания, несмотря на отсутствие реально произведенных измерений. В результате будут получены значения средних квадратических погрешностей положения всех точек хода, а также эллипсы ошибок их положения. При данном виде обработки проектных данных искомые параметры будут найдены на порядок быстрее, но вопрос о негативных факторах все также остается открытым.

Оба способа достаточно просты, что является их преимуществом, но они показывают лишь предполагаемую величину возможной ошибки и не дают подробной информации о том, что ее провоцирует. Также в ходе такого предрасчета точности сети не учитывается возможность возникновения ошибок, имеющих значения выше ожидаемых.

Иным способом предрасчета точности точек хода является оценка внешней и внутренней надежности измерений. Данная оценка может производиться по элементам матриц линейных преобразований. Внутренняя надежность показывает контролируемость элементов сети от искажающих факторов – то значение минимальной грубой ошибки, которую можно будет выявить с заданной вероятностью. Основным способом повышения внутренней надежности измерений является увеличение числа избыточных измерений, но в маркшейдерской практике зачастую нет возможности повысить избыточность построения, а повышение точности измерений не всегда дает желаемый результат. Поэтому целесообразнее при проектировании линейно-угловых сетей контролировать не выявляемость тех или иных ошибок, а степень их влияния на определяемые параметры, о которой позволяют судить параметры внешней надежности построения. 

Внешняя надежность показывает влияние невыявленной в ходе уравнивания единицы ошибки на определяемые параметры. Оценка этого параметра важна при низкой контролируемости измерений (внутренней надежности), так как возможно неполное исключение грубых ошибок измерений, что повлияет на точность определяемых по результатам съемки параметров. 
Одним из наиболее распространенных способов обработки данных геодезических и маркшейдерских съемок является метод наименьших квадратов. В матричном изложении принцип наименьших квадратов выражается в следующем равенстве [3, 4]:

,       (3)

где V – матрица поправок в измеренные значения, P – матрица весов измеренных величин. 

При этом система параметрических уравнений поправок имеет вид:V = AT + L, (4)где A – матрица коэффициентов параметрических уравнений поправок; L – вектор свободных членов уравнений поправок; T – вектор поправок в параметры.

В ходе математических преобразований можно выявить прямоугольную матрицу линейных преобразований В [3, 4]:

В = –QA^TP = ,      (5)

где Q – матрица обратных весов измерений, n – число измерений, t – число неизвестных параметров. 

Так как матрица B является переходным элементом от вектора свободных членов L к вектору поправок T, в ней содержится информация о том, как невыявленные грубые промахи будут влиять на определяемые параметры, что соответствует смыслу внешней надежности [3].

Каждый элемент матрицы В показывает величину, на которую исказится определяемый параметр ввиду наличия невыявленной ошибки в измерении, при этом размерность искажения соответствует размерности исходных данных, а величина ошибки равна единице. Таким образом, элемент матрицы b₁₂ показывает, насколько исказится первый определяемый параметр при наличии во втором измерении 1 мм или 1” ошибки. 

Как видно из формулы, элементы матрицы линейных преобразований B зависят от точности измерений, заложенной в весовой матрице P, и от геометрических параметров съемочного построения, отражающихся в значениях элементов матрицы поправок параметрических уравнений A. Таким образом, повысить надежность линейно-угловой сети на этапе ее проектирования можно изменением точности измерений, а также геометрии построений. 
Что немаловажно, в матрице B заключены значения степени влияния ошибки в любом из измерений на каждый из определяемых параметров, что позволяет провести полноценный анализ уровня надежности сети, оценив не только максимальное значение искажения результатов в случае наличия промахов, но поведение любого из элементов построения, что невозможно при классической оценке точности проектируемых сетей. Более того, с использованием данной матрицы возможно перейти от анализа влияния лишь грубых промахов к оценке искажений результатов от любой по величине ошибки.

На стадии проектирования анализ матриц линейных преобразований позволяет определить, какие измерения требуют повышенного внимания и точности. Также иногда выявляются измерения, не требующие повышенной точности измерений, заявленной в инструкциях, что может снизить время производства работ. Таким образом, оценивая внешнюю надежность проектируемой сети, можно до начала производства работ подобрать наиболее рациональную методику съемки (например, сокращение/увеличение числа приемов измерений одного угла или повторных линейных измерений одной и той же стороны) и геометрию построения, которые будут удовлетворять требованиям рекомендаций и инструкции, а также будут учитывать возможность возникновения значительных по величине ошибок. 
Для удобства можно использовать дополнительную матрицу S [3]:

S = BM,      (6)

где М – диагональная матрица погрешностей измерений. 

Каждый элемент матрицы S отражает, как повлияют на определенные параметры ошибки измерений, равные ожидаемым. Эти ошибки уже непосредственно можно сравнить с допустимыми погрешностями измерений. 

Таким образом, в дополнение к классической «точечной» оценке точности, оценка внешней надежности на этапе проектирования сети позволяет:

1. провести полноценный анализ уровня надежности сети, т.е. поведение любого из элементов построения;
2. подобрать рациональную методику съемки, геометрию построений, а также оптимальное число избыточных измерений;
3. анализировать искажение определяемых параметров от любых по величине ошибок измерений;
4. перейти от степени влияния единицы невыявленной ошибки на определяемые параметры непосредственно к погрешности положения каждого пункта сети.

1. Инструкция по производству маркшейдерских работ (РД 07 603 03). Серия 07. Вып. 15.  / Колл. авт. – М.: Федеральное государственное унитарное предприятие «Научно-технический центр по безопасности в промышленности Госгортехнадзора России», 2004. – 120 с.
2. Зверевич В.В., Гусев В.Н., Волохов Е.М. Анализ точности подземных маркшейдерских сетей. Учебное пособие. Санкт-Петербург: РИЦ СПбГГИ(ТУ), 2014,-145 с.
3. Алексенко А.Г. Разработка методики оценки и повышения внешней надежности маркшейдерских съемочных построений: дис. … канд. техн. наук: 25.00.16 / А.Г. Алексенко. – СПб, 2015. – 136 с.
4. Алексенко А.Г., Зубов А.В. Проектирование маркшейдерско-геодезических сетей с учётом параметров надёжности // Маркшейдерский вестник.-2014.-№5. – с.31-32.

Все статьи автора «Алексенко Анастасия Геннадьевна»