Статья подготовлена по материалам доклада, представленного на XLII Академических чтениях по космонавтике, посвященных памяти академика С.П. Королёва и других выдающихся отечественных ученых — пионеров освоения космического пространства. Москва, МГТУ им. Н.Э. Баумана, 23–26 января 2018 г.
Введение
С 1964 г. к Марсу было направлено около 30 космических аппаратов (КА) и 23 из них достигли Красной планеты (см. табл. 1). Но публикации, детально описывающие траектории этих полетов, отсутствуют. Единственно, что нам известно – это даты старта космических кораблей с Земли и даты пресечения ими орбиты Марса или перехода на марсианские орбиты. Тем более интересной представляется реконструкция перелётных орбит для уже состоявшихся запусков.
Таблица 1. Важнейшие экспедиции к Марсу (Данные, включённые в эту таблицу, получены с Интернет-сайтов «Википедия» (ru.wikipedia.org/) и Jet Propulsion Laboratory (mars.jpl.nasa.gov/). Конкретные ссылки не приводятся с целью экономии места.)
|
Наименование экспедиции |
Дата запуска |
Дата прилёта |
Результат |
| Mariner-4 |
28.11.1964 |
15.07.1965 |
Пролетел мимо Марса на расстоянии9846 км |
| Mariner-6 |
24.02.1969 |
31.07.1969 |
Пролетел мимо Марса на расстоянии3431 км |
| Mariner-7 |
27.03.1969 |
05.08.1969 |
Пролетел мимо Марса на расстоянии3430 км |
| Марс-2 |
19.05.1971 |
27.11.1971 |
Стал искусственным спутником Марса (ИСМ) с Т = 18 час. |
| Марс-3 |
29.05.1971 |
02.12.1971 |
Стал ИСМ с Т = 12 час. 16 мин. |
| Mariner-9 |
30.05.1971 |
1311.1971 |
Стал ИСМ (параметры орбиты неизвестны) |
| Марс-4 |
21.06.1973 |
10.02.1974 |
Пролетел мимо Марса на расстоянии1844 км |
| Марс-5 |
25.07.1973 |
12.02.1974 |
Стал ИСМ (параметры орбиты неизвестны) |
| Марс-7 |
09.08.1973 |
09.03.1974 |
Пролетел мимо Марса на расстоянии1400 км |
| Viking-1 | 20.08.1975 |
19.06.1976 |
Стал ИСМ с Т = 24,66 час. |
| Viking-2 | 09.09.1975 |
07.09.1976 |
Стал ИСМ с Т = 24,6 час. |
| Фобос-2 | 12.07.1988 |
29.01.1989 |
Стал ИСМ с Т = 77 час. |
| Mars Global Surveyor | 07.11.1996 |
11.09.1997 |
Стал ИСМ с высотой орбиты378 км |
| Mars Pathfinder | 04.12.1996 |
04.07.1997 |
Мягкая посадка, спуск марсохода Sojourner |
| Mars Odyssey | 07.04.2001 |
24.10.2001 |
Стал ИСМ с Т = 1,964 час. |
| Mars Express | 02.06.2003 |
20.12.2003 |
Стал ИСМ с Т = 6,7 час. |
| Spirit | 10.06.2003 |
03.01.2004 |
Мягкая посадка на Марс |
| Opportunity | 08.07.2003 |
25.01.2004 |
Мягкая посадка на Марс |
| Mars Reconnaissance Orbiter | 12.08.2005 |
10.03.2006 |
Стал ИСМ. Т = 35,5 час.
Перицентр –3806 км, апоцентр –47972 км |
| Mars Science Laboratory | 26.11.2011 |
06.08.2012 |
Мягкая посадка и спуск марсохода Curiosity |
| Mars Atmospheric and Volatile Evolution (MAVEN) | 18.11.2013 |
21.09.2014 |
Стал ИСМ |
| Mangalyaan | 30.11.2013[*] |
24.09.2014 |
Стал ИСМ с Т = 72 час. 52 мин. |
| ЭкзоМарс-2016 | 14.03.2016 |
19.10.2016 |
Жёсткая посадка спускаемого аппарата |
[*] Переход на гелиоцентрическую орбиту (по другим КА эта дата не приводится).
Метод решения задачи
В общем случае, небесное тело в центральном поле силы тяготения движется по эллиптической орбите (первый закон И. Кеплера [1]). Если мы придадим КА, находящемуся на границе гравитационной сферы Земли, определённое ускорение, то он перейдёт на гелиоцентрическую эллиптическую орбиту. В работе [2] был описан алгоритм, позволяющий найти параметры эллипса, если заданы два его радиус-вектора, выходящие из одного фокуса (см. рис. 1). Т.о. задав одну точку на орбите Земли (точка В), а вторую – на орбите Марса (точка С), мы можем найти множество эллипсов, проходящих через эти две точки с определёнными величинами длины большой оси и эксцентриситета.

Рисунок 1. Перелётная орбита между двумя эллиптическими орбитами.
По круговой орбите небесное тело движется со скоростью, определяемой уравнением:
м – гравитационный параметр центрального тела,
r – длина радиус-вектора движущегося тела относительно центрального.
Для эллиптической орбиты это уравнение справедливо в двух точках, когда угол между большой осью эллипса и радиус-вектором равен 90°. При этом длина радиус-вектора равна фокальному параметру эллипса р:
a – длина большой полуоси,
b – длина малой полуоси.
Вычислить круговую скорость тела в любой точки орбиты мы можем воспользовавшись законом сохранения момента количества движения (углового момента) [3, с. 97]:
Длина радиус-вектора точки на эллиптической кривой относительно фокуса эллипса в зависимости от величины угла (обозначим его Θ), отсчитываемого от перицентра эллипса, может быть вычислена по уравнению [4, с. 50]:
Далее, для выбранных параметров эллипса мы можем найти длину дуги, соединяющей заданные точки
Теперь, зная скорость тела в любой точке, мы можем найти время движения тела по дуге ВС, вычислив интеграл [2]:
.gif) . (5)
. (5)В представленных ниже результатах расчётов интегрирование было выполнено численным методом с шагом 0,0001 от величины угла BAC.
Движение небесного тела по эллиптической орбите характеризуется не только круговой скоростью, которая связана с угловой скоростью ω соотношением:
но и радиальной vR, описывающей движение тела вдоль оси радиус-вектора.
Эту величину мы также должны учитывать при расчёте импульсов скоростей разгона и торможения. Радиальная скорость vR может быть найдена на основании закона сохранения полной механической энергии, который мы можем представить в следующем виде [5]:
Отсюда:
Величину полной энергии можно вычислить в точках апсид эллипса, в которых радиальная скорость равна нулю.
Суммарная величина импульса скорости разгона («торможения») вычислена из суммы квадратов импульсов для радиальной и круговой скоростей.
Орбита Марса наклонена к плоскости орбиты Земли (плоскости эклиптики) на 1,85°. Следовательно, или точка прилёта должна совпадать с узлом орбиты Марса или мы должны изменить плоскость перелётной орбиты, придав КА дополнительное движение, перпендикулярное плоскости эллиптической орбиты. Величина ускорения может быть найдена по уравнению [2]:
Δφ – изменение угла наклона плоскости орбиты,
Δt – время, за которое произошло изменение угла наклона плоскости орбиты.
Если мы примем Δφ равным широте Марса в точке прилёта, а Δt равным времени перелёта, то приблизительную величину соответствующего импульса скорости можно будет найти по формуле:
![]() – средняя круговая скорость.
– средняя круговая скорость.
Эфемериды Земли и Марса были найдены по программе Planeph 4.2 [6].
Результаты и их обсуждение
Для всех 23 экспедиций были найдены:
- эфемериды (по программе Planeph 4.2) Земли на дату старта и Марса на дату прилёта (долготы, широты, радиусы орбит, угловая и радиальная скорости);
- параметры перелётного эллипса, дающего совпадение по времени перелёта с литературными данными (длина большой полуоси, эксцентриситет, углы точек В и С относительно перицентра эллипса);
- параметры движения по эллиптической орбите (длина дуги, угловой момент, полная механическая энергия, время полёта, круговая и радиальная скорости в точках отлёта и прилёта);
- импульсы скоростей разгона и «торможения»;
- расстояние между Марсом и плоскостью эклиптики в точке прилёта и величина импульса скорости, необходимая для изменения плоскости орбиты.
При этом нужно учитывать, что собственно эллиптическая перелётная орбита начинается в момент выхода КА из гравитационной сферы Земли и заканчивается в момент входа КА в гравитационную сферу Марса. Момент перехода с геоцентрической на гелиоцентрическую орбиту приводится только для Mangalyaan. Для остальных экспедицией эти данные отсутствуют, как и даты вхождения КА в гравитационную сферу Марса. Для Mangalyaan переход на гелиоцентрическую орбиту по спиральной орбите продолжался 25 суток – с 5 по 30 ноября 2013 г. Поэтому нельзя утверждать, что в результате проведённого исследования удалось найти истинные траектории перелётных орбит приведённых выше экспедиций к Марсу. Эта статья скорее демонстрирует возможности разработанной методологии проектирования и анализа эллиптических орбит.
Для старта КА к Марсу были использованы почти все зоны земной орбиты. Наибольшей популярностью обладают сектора в диапазонах от 45 до 70° (6 запусков), 238259° (5 запусков) и 285319° (5 запусков) Отсчёт долгот идет от точки осеннего равноденствия Земли (23 сентября).
На эллипсе перелётной орбиты положение точек запуска находится вблизи его перицентра в диапазоне от -45 (Mars Odyssey) до +29° (Mariner-7), 10 запусков – в диапазоне от -6 до +6°. Точка запуска Mars Pathfinder приходится почти точно на перицентр (0,1°).
Угол перелётной орбиты варьировался в широком диапазоне – от 101 (Mariner-7) до 236° (Mars Odyssey). Но длина большой полуоси перелётного эллипса лежит в более узких пределах – от 174 (Mars Odyssey) до 202 млн. км (Mars Reconnaissance Orbiter). При этом длина орбиты (длина дуги на перелётном эллипсе) зависит не только от длины большой полуоси эллипса, но и от положения дуги на эллипсе. Наименьшая длина дуги перелётной орбиты, как и следовало ожидать, у Mariner-7 – 310 млн. км, наибольшая – у MAVEN – 705 млн. км при среднем значении 524 млн. км. Для большинства запусков она находится в диапазоне от 300 до 500 млн. км. Экспедиция Mariner-7 также характеризуется высокой средней орбитальной скоростью – 27,4 км/с. В целом, разброс скоростей невелик – от 24,4 (Viking-2) до 28,4 (Mariner-6) км/c при среднем значении 26,6 км/с. Время перелёта находится в диапазоне от 131 (Mariner-7) до 333 (Viking-2) сут. при среднем значении 230 сут.
Следующий важный момент – это энергетические затраты, необходимые для осуществления экспедиции, характеризующиеся импульсом скоростей. Максимальный суммарный импульс был у Mariner-7 – 12,6 км/с, минимальный – у Spirit – 3,6 км/с. Для 16 экспедиций он находится в диапазоне 68 км/с. Кроме Spirit меньший импульс скоростей требовался для Mars Express (5,6 км/с), для остальных 5 он превышал 8,0 км/с.
Импульс скорости, необходимый для изменения наклона плоскости орбиты, не превышает 0,8 км/с. В некоторых случаях, когда точка прилёта близка к узлу орбиты Марса (Mariner-4, Mars Pathfinder, Mars Express, Spirit, Mars Science Laboratory), он менее 0,1 км/с, так что для выполнения этого манёвра можно использовать двигатели малой тяги.
Импульс скорости разгона при отлёте из гравитационной сферы Земли складывается из двух составляющих, связанных с круговой и радиальной скоростями. Во всех случаях, для перехода на траекторию перелётного эллипса требуется увеличение круговой скорости. Минимальный импульс для круговой скорости требовался Spirit (1,1 км/с), максимальный – Mars Reconnaissance Orbiter (3,7 км/с).
Для радиальной скорости диапазон несколько шире: от 0,05 до 3,8 км/с. Эллиптическое движение включает 4 фазы:
1) на участке от 0 до 90° считая от перигелия идёт увеличение радиальной скорости, направленной от Солнца;
2) на участке от 90 до 180° радиальная скорость уменьшается до 0;
3) на участке от 180 до 270° радиальная скорость вновь увеличивается, но уже в направлении к Солнцу;
4) на участке от 270 до 360° радиальная скорость уменьшается до 0.
Минимальное значение импульса мы имеем в том случае, когда фазы движения небесного тела на орбите Земли и на орбите перелётного эллипса совпадают. Такие результаты были получены для Марс-2 (ΔvR = 0.05 км/с) и Spirit (0.08 км/c). В целом, для 17 запусков из 23 импульс радиальной скорости не превышает 1,5 км/с. Наибольшее значение (3,8 км/с) получено для Mars Odyssey. КА аппарат стартовал от Земли, когда она находилась вблизи перигелия, а на перелётном эллипсе начальная точка орбиты отстояла от перицентра на 45°.
При подлёте к Марсу во всех случая круговая скорость КА оказывается меньше, чем у Марса, в среднем на 2,7 км/с. Поэтому термин «импульс скорости торможения» носит условный характер. Т.о., чтобы перейти на марсоцентрическую орбиту КА должен увеличить свою скорость. Наибольшее отставание было Mariner-7 – 4,3 км/с, наименьшее – у Mars Reconnaissance Orbiter – 1,9 км/с.
Для радиальной скорости расхождения оказываются значительно больше, чем при отлёте от Земли – до 6,7 км/с (Mariner-6, Mariner-7). Но в ряде случаев точка прилёта была выбрана удачно (Марс-2, Марс-3, Марс-4, Марс-7, Mars Global Surveyor, Mars Express, Spirit, Opportunity, MAVEN, Manglyaan), так что импульс скорости торможения не превышал 1 км/с.
Из 23 запусков, приведённых в табл. 1, в 5 случаях КА пролетел мимо Марса. Это Mariner-4, Mariner-6, Mariner-7, Марс-4 и Марс-7.
Причина неудач для Mariner-6 и Mariner-7 очевидна: это большая радиальная скорость на перелётной орбите, к тому же имевшая направление, противоположное радиальному движению Марса. Параметры движения Марс-4 и Марс-7 при сближении с Марсом не отличались принципиально от параметров Марс-5, который стал спутником Марса. Но переход с гелиоцентрической орбиты на планетоцентрическую имеет сложную природу и требует специального рассмотрения.
Тем не менее, можно утверждать, что меньшие энергетические затраты требуются при использовании перелётного эллипса с меньшим эксцентриситетом. В работе [2] был сделан поспешный вывод о том, что эксцентриситет перелётного эллипса увеличивается с увеличением длины его большой полуоси. Анализ большего массива данных показал, что типичная зависимость e от a включает минимум. Минимальная величина суммарного импульса скоростей разгона и торможения не обязательно приходится на перелётный эллипс с минимальным эксцентриситетом, но находится вблизи него.
На рис. 2 представлены результаты расчётов, выполненных для различных перелётных эллипсов, проходящих через точки запуска и прилёта КА “Mariner-6”. Минимальное значение эксцентриситета (0,200) достигается при длине большой полуоси перелётного эллипса 1,801,82·1011 м, а минимальный импульс скоростей (8,2 км/с) при длине большой полуоси 1,791,80·1011 м. Для этих орбит время перелёта находится в интервале от 179 до 172 сут. по сравнению со 157 сут. реального перелёта. Этому времени соответствует эллипс с длиной большой полуоси 1,93·1011 м и эксцентриситетом, равным 0,231; суммарный импульс скоростей 10,3 км/с. Нужно подчеркнуть, что только этот эллипс позволяет достичь орбиты Марса в нужный момент, когда в точке прибытия находится сама планета.
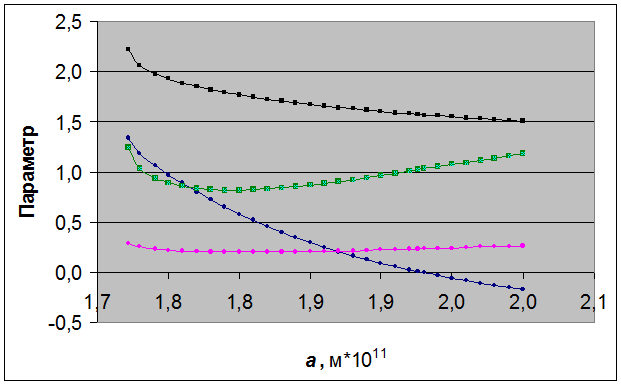
Рисунок 2. Параметры перелётных эллипсов для Mariner-6 в зависимости от длины большой полуоси (1 – время перелёта, сут.·100; 2 – угол между перицентром и началом перелётной дуги, рад.; 3 – суммарный импульс скоростей, км/с·10, 4 – эксцентриситет).
Заключение
В работе найдены перелётные эллипсы и параметры орбитального движения, дающие совпадение по времени перелёта с данными, приводимыми в литературе для 23 состоявшихся экспедиций к Марсу.
Проведённое исследование демонстрирует возможности метода проектирования и оптимизации перелётных эллиптических орбит.
Статья подготовлена по материалам доклада, представленного на XLII Академических чтениях по космонавтике, посвященных памяти академика С.П. Королёва и других выдающихся отечественных ученых — пионеров освоения космического пространства. Москва, МГТУ им. Н.Э. Баумана, 23–26 января 2018 г.
Библиографический список
- Драчев М.М., Демин В.Г., Климишин И.А., Чурагин В.М. Астрономия. – М.: «Просвещение», 1983, с. 89.
- Островский Н.В. Алгоритм нахождения траектории перелёта между двумя эллиптическими орбитами. // Инженерный журнал: наука и инновации, 2017, № 6 [электронный ресурс]. URL: http://dx.doi.org/10.18698/2308-6033-2017-6-1666 (дата обращения 09.04.2018).
- Митишов Е.А. Берестова С.А. Теоретическая механика: статика, кинематика, динамика. – М.-Ижевск: Институт компьютерных исследований, 2005. – 176 с.
- Александров А.Д. Нецветаев Н.Ю. Геометрия: учебное пособие. – М.: Наука, гл. ред. физ.-мат. лит., 1990. – 672 с.
- Островский Н.В. Проверка принципа эквивалентности общей теории относительности. // Статьи по теоретической физике. – Saarbrűcken, Lambert academic publishing, 2016, с. 30-34.
- Сhapront J., Francou G. Ephemerides of planets between 1900 and 2100 (1998 update). Bureau des Longitudes, Group: Dynamics of Solar System (1996). URL: http://cdsarc.u-strasbg.fr/viz-bin/Cats?/VI/87/ (date of the application 09.02.2017).
