ВОЛНЫ ДЕ БРОЙЛЯ. ИЛЛЮСТРАЦИЯ

Обозначим проблемные (с нашей точки зрения) моменты, которые имеют место быть в механике в настоящее время.

1. За основные физические величины, относящиеся к области механики, приняты единицы длины, времени и массы. При всем этом, изучая движение тел (частиц) относительно какой – либо системы отсчета, мы, как ни странно, совершенно не находим в ней отображения третьей основной единицы измерения – массы, хотя по определению массой обладают как сами тела (частицы), изучением движения которых мы занимаемся, так и системы отсчета.

2. Объективная реальность, обозначаемая в научном мире термином «волны де Бройля», является чисто умозрительной. И в системах отсчета эта реальность никоим образом не отображается. Наглядность математической модели волн, сопутствующих материальным частицам, сделала бы это физическое явление более доступным для понимания.

Чисто логически можно думать, если опытные факты говорят, что корпускулярно – волновыми свойствами обладают все без исключения микрочастицы и системы, состоящие из них, то это явление природы должно быть каким – то образом связано со свойствами пространственно – временного континуума.

Пусть на псевдоевклидовой плоскости 4-х мерного пространства Минковского имеем условно неподвижную пространственно – временную систему отсчета , обозначим ее K. И движущуюся относительно нее со скоростью Vвдоль положительного направления пространственной оси x систему отсчета  (система ). Для упрощения условимся, что моменты ,  и начала ,  этих систем совпадают (рис 1). И часы в этих системах в данный момент времени синхронизируются.

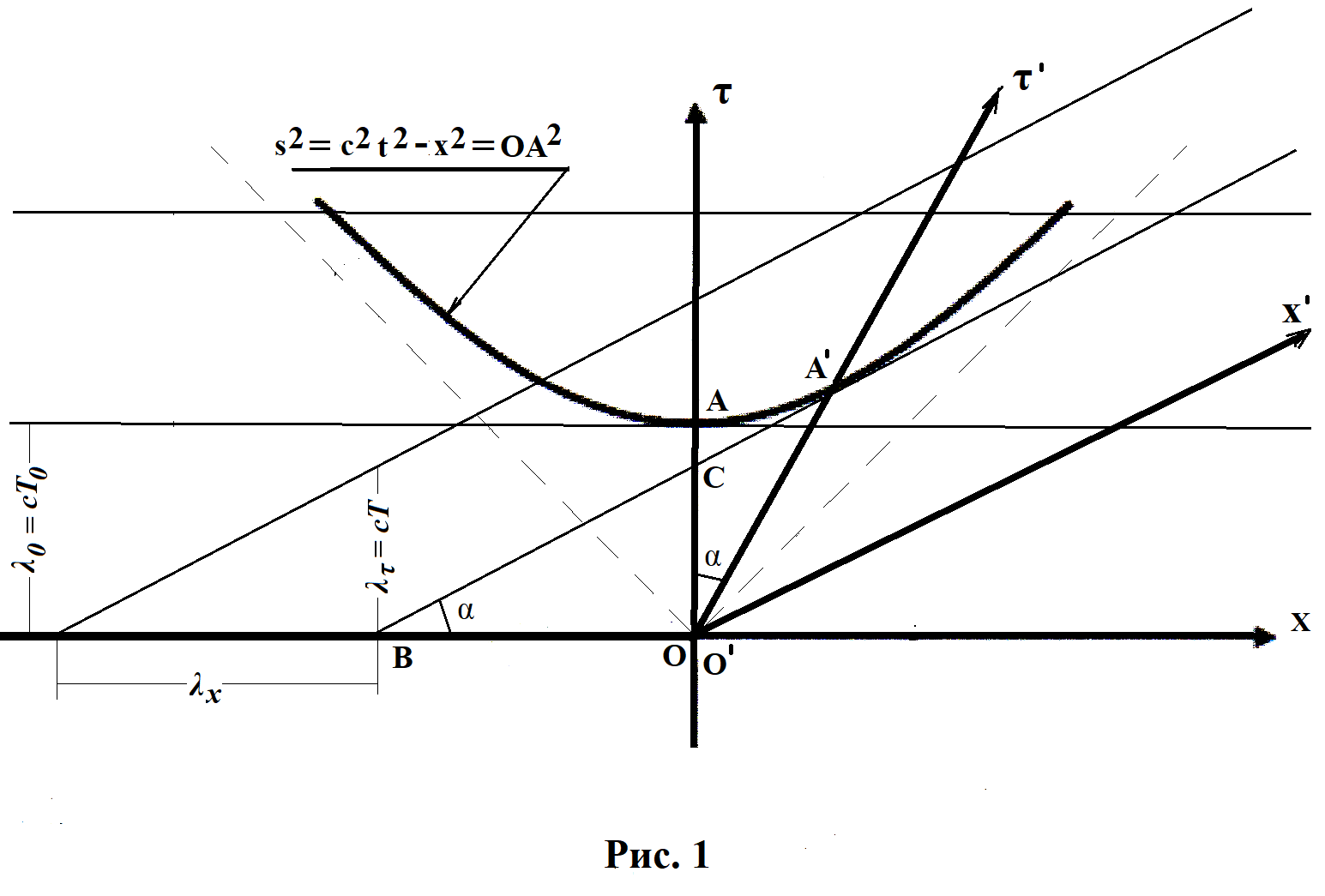
Согласно СТО А. Эйнштейна, геометрическим местом точек “равноудаленных” от начала координат на псевдоевклидовой плоскости будут четыре гиперболы: , . В нашем случае на рис.1 изображена масштабная гипербола . Временная ось  системы  пересекается с данной гиперболой в точке  и определяет масштабный отрезок  этой оси, равный на псевдоевклидовой плоскости отрезку OA. Через точку проведем линию одновременности в системе , (которая должна быть параллельна оси ). Она пересекается с осью системы K в точке C, а с осью x этой же системы – в точке B. Эта линия наклонена к оси x под углом , где V – скорость, с которой перемещается система  относительно К, c – скорость света. На рис. 1 сразу же видим, что ОС меньше единичного отрезка . (1)

Из СТО следует, что  в  раз, т.е.

 (2)

Откуда: . (3)

Принимая во внимание (1), и что , а так же учитывая, что , перепишем (3) как:

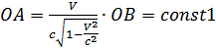. (4)

Левая часть полученного нами равенства есть величина постоянная, т.к. по условию OA – единичный временной отрезок. Следовательно, и правая часть этого равенства должна быть величиной, не зависящей от скорости перемещения системы . Рассмотрим подробнее.

При  координатные оси движущейся системы , словно лезвия ножниц, раздвигаются относительно биссектрисы квадранта, а угол б наклона оси  к оси  стремится к нулю. Точка  пересечения оси  с единичной гиперболой стремится к A. При этом линия одновременности системы , проходящая через точку , стремится совпасть с линией одновременности, проходящей через точку A, которая параллельна оси x. Или иначе, точка B пересечения линии одновременности системы  с осью x устремляется в бесконечность. Кратко: при ,

; . (5)

Далее. Если , тогда координатные оси системы  (опять же, словно лезвия ножниц) сдвигаются к биссектрисе квадранта, и точка  пересечения оси  с единичной гиперболой, ветвь которой асимптотически приближается к биссектрисе, устремляется в бесконечность. Линия одновременности, проходящая через эту точку, стремится совпасть с биссектрисой квадранта. При этом точка B пересечения этой линии с осью x стремится к началу O. Кратко: при ,

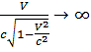; . (6)

Видим, при изменении скорости движения системы отсчета  в пределах, соответствующих условиям (5), когда получается неопределенность вида  и (6) – неопределенность вида , увеличение одного из сомножителей правой части равенства (4) должно соответствовать уменьшению другого. И, в конечном итоге, произведение этих сомножителей должно иметь конечную величину, равную OA.

В физике система координат не абстрактное понятие. Физическая система отсчета – это всегда материальное тело, имеющее массу покоя. Или, что одно и то же, с любой материальной частицей с ненулевой массой покоя можно связать систему отсчета. Будем считать, что рассматриваемая нами система  связана с частицей массой m. Умножим обе части(4) на инвариантные величины m и c, получим:

. (7)

Где 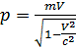 – импульс массы m,

 - имеет размерность момента количества движения.

Отрезок OB – это один из множества равных отрезков, определяемых пересечением с осью x множеством линий одновременности системы , проведенных через концы равных единичных временных отрезков оси  этой системы отсчета. На рис 1, во избежание загромождения рисунка, показаны только две линии одновременности (не считая линию одновременности ) и два отсекаемых ими отрезка на оси x. Величину OB назовем пространственным промежутком между линиями одновременности. Если предположить, что (7) - это и есть соотношение, постулируемое Луи де Бройлем для материальных частиц и OB характеризует длину волны, тогда , где h – постоянная Планка. И из (7) тотчас же следует: , откуда:

. (8)

Это есть Комптоновская длина для покоящейся массы.

Обозначим  через , где  – единичный отрезок времени. Тогда из (8) следует:

.

Где  – энергия покоящейся массы m, .

Множество отрезков на оси  равных OC (на рис.1 показаны только два отрезка) обозначим как . Назовем их временными промежутками между линиями одновременности. Учитывая это, а так же (1), (2) и (8) получим: 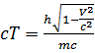, откуда:

.

Где  - полная энергия движущейся массы m; .

Поскольку единичному временному отрезку OA сопоставляется длина , то очевидно, должна речь идти о некоем периодическом процессе во времени. Обсуждение возможных толкований этого физического процесса не является целью данной статьи. Но заострим внимание лишь на том, что любой цикл подразумевает фазу. Для упрощения, чисто с методологической точки зрения, можно принять за цикличный процесс вращение стрелки часов. За период  стрелка непрерывно и равномерно меняет свое положение (фазу) относительно положения, условно принятого как начальное. В этом случае линии одновременности, проходящие через концы временных промежутков  параллельно оси x (и временных промежутков  параллельно оси  системы ) можно трактовать как линии равнофазные (линии равных фаз).

Фазовая скорость волны  относительно оси x легко определяется из треугольника OBC:

.

Фаза волны имеет обычный вид:

.

Перейдем к рассмотрению пересечения осью  системы  единичной гиперболы  (рис. 2).

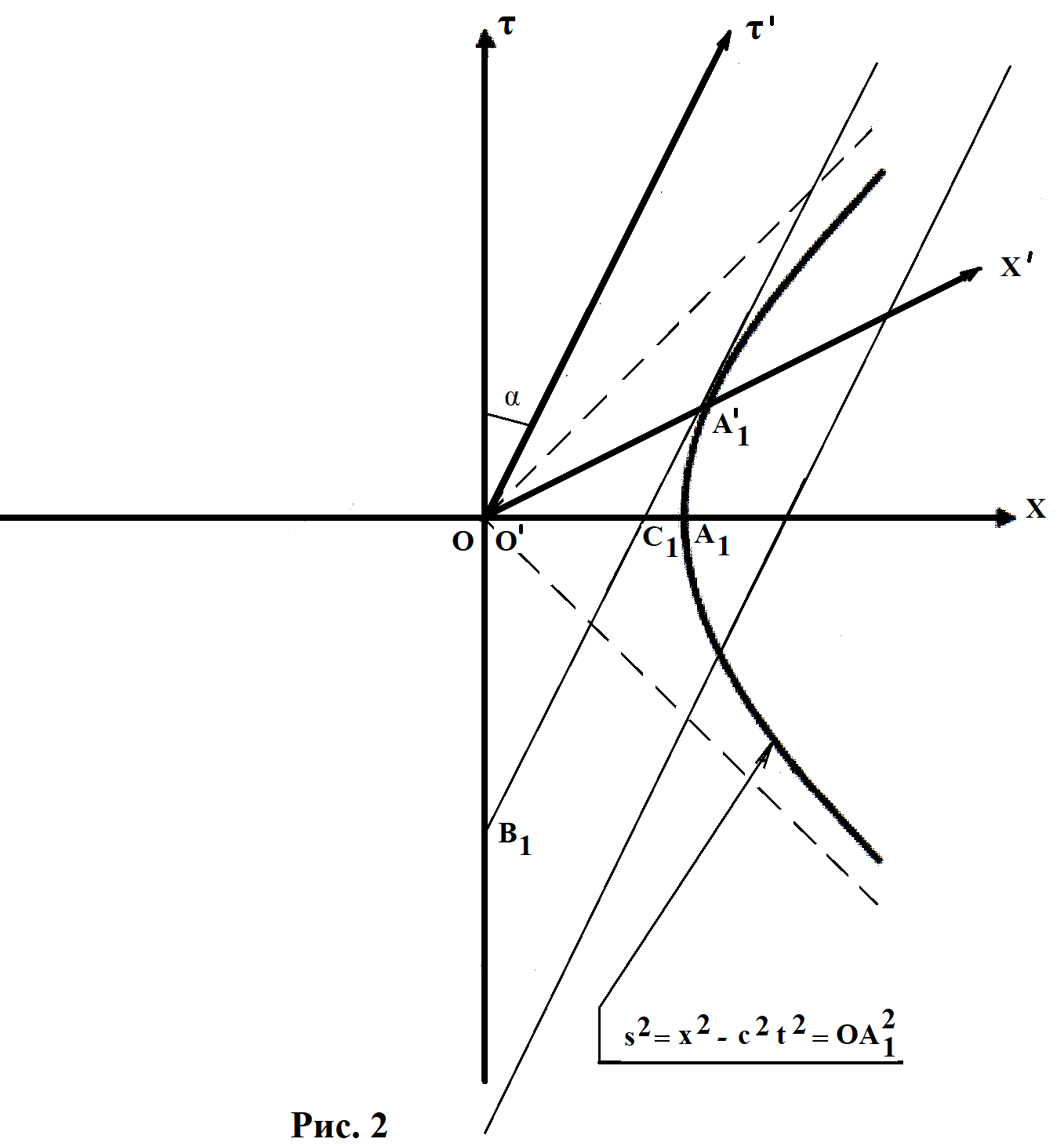
Точка  пересечения координатной оси с единичной гиперболой определяет единичный отрезок  оси , равный на псевдоевклидовой плоскости длине . Линии, проведенные через концы множества единичных отрезков этой оси параллельно временной оси , пересекая ось , дают нам множество отрезков, равных . Рассуждая аналогично, как мы это делали для гиперболы , получим соотношение:

.

Откуда:  и, согласно положениям СТО: .

А это означает, что с точки зрения системы K координатная сетка системы отсчета  имеет ячейки, размеры которых будут, принимая во внимание рис 1: .

Подведем итог всему выше изложенному.

1. Покоящейся частице сопоставляется область пространственно – временного континуума, в которой происходит цикличный процесс во времени. Эту “оцифрованную” область мы и называем “система отсчета, связанная с материальной частицей”. Координатные оси этой системы имеют естественные единицы длины, по величине обратно пропорциональные энергии покоя частицы.

2. С точки зрения системы отсчета, имеющей движение относительно системы, связанной с покоящейся частицей, периодический цикличный процесс в этой, условно неподвижной системе, происходит не только во времени, но и в пространстве с длиной волны, величина которой обратно пропорциональна импульсу частицы. При этом естественной единицей длины координатных осей системы, которой сопоставляется частица, будут величины, обратно пропорциональные полной энергии частицы.

3. Исходные пункты квантовой механики изначально заложены в теории относительности А. Эйнштейна 1905 года. В то время как основные положения этой механики, т.е. идея (постулат) о волновых свойствах частиц была выдвинута Луи де Бройлем лишь 19 лет спустя. Этот факт является еще одним веским аргументом в пользу состоятельности СТО.

---

Количество просмотров публикации: Please wait

Все статьи автора «Дружинин Дмитрий Алексеевич»