Идет активная работа по разработке квантовых компьютеров. Данные компьютеры, используя алгоритм Шора, могут легко взломать системы основанные на факторизации целых чисел. Соответственно самая распространённая криптосистема открытого ключа RSA является уязвимой [1].
Альтернативой RSA для пост квантовой эпохи являются крипто системы, основанные на хешировании. Безопасность, которых основывается на безопасности хеш-функции. Были предложены системы одноразовых подписей [2]
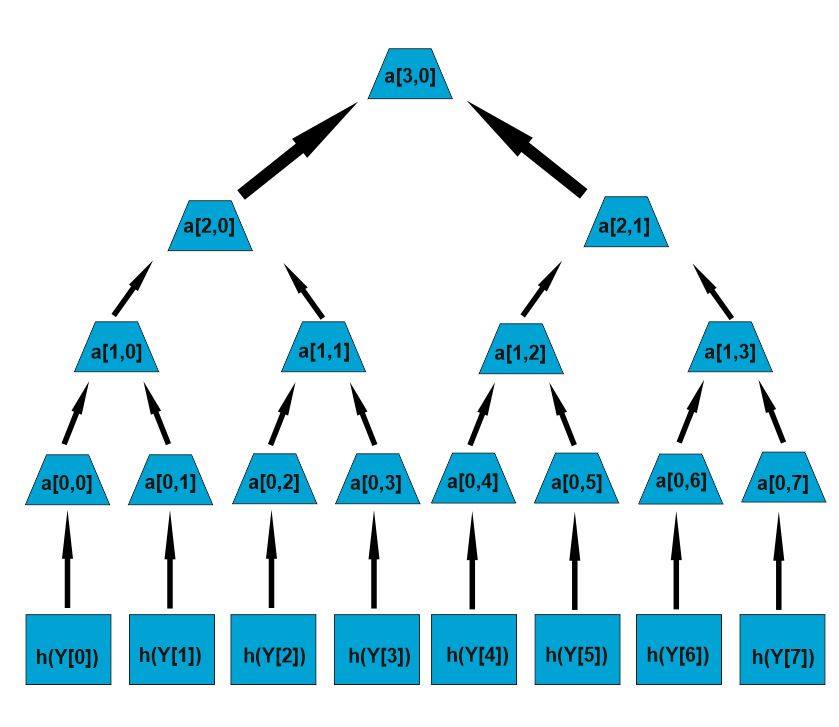
Данные системы являются неэффективными из-за, передачи открытого ключа множество раз. Криптосистема Меркле улаживает эту проблему. В этой системе один и тот же открытый ключ используется для шифрования множества сообщений. В данной системе генерируются ключи Xi и Yi для N записей и вычисляется hi=h(Yi), и строится дерево Merkle[3,4].
В данном дереве последующий узел является хешированием объединения своих потомков. a1,0 = h(a0,0|| a0,1); Корень дерева an,0 является открытым ключом public.
Для того, чтобы получить подпись мы используем криптосистему одноразовой подписи и объединяем ее с каждым братским узлом. sig = (signew ||auth0||auth1||…||authn−1). Для верификации подписи проверяется одноразовая подпись и открытый ключ, используя братские узлы.
Мы реализовали данный алгоритм, на языке программирования Python, ниже приведен псевдо код данной реализации:
· Importing necessary libs
· Define class
· Defining “ alt_hashes(hashes) “ method
· Set list “ arr ”
· If hashes == “ ”, raise Exception
· Foreach loop
o sorting hashes and appending into arr
· Length_of_block == length of arr
· While loop, if length is odd, copy last element in list
o append it into arr list
· Set list “ another_arr ”
· Foreach loop
o For loop with range from 0 to length of “ arr “ and iteration by 2
§ Define variable with “ sha512() “ value
§ Hash elements that are in “ arr “ list
§ Apennd them into new “ another_arr “ list
§ Return this listin hex
· Set list “ hash_arr ”
· Foreach loop
o Generate Hex and put it into “ hash_arr ” list
· Create message put it in “ st “ variable
· Convert “ st “ value in binary
· First_secret_key = hash_arr[0]
· Second_secret_key = hash_arr[1]
· Generate “ one-time signature ”
o If st == 0
§ Choose “First_secret_key “ bit
o Else
§ Choose “Second _secret_key “ bit
· First_pub_key = hash(hash_arr[0])
· Second_pub_key = hash (hash_arr[1])
· Encryption
o Concatenate “ one-time signature ” with message’s hash
· Verification of “ one-time signature ”
o If bit of “ one-time signature ” == 0
§ Compare with “First_secret_key “ bit
o Else
§ Compare with “Second _secret_key “ bit
· Verification of “ signature ”
o Concatenate siblings with each other
o If this equals to public key
§ Sign is correct
o Else
§ Sign is not correct
РАБОТА ВЫПОЛНЕНА В РАМКАХ НАУЧНОГО ГРАНТА «НАЦИОНАЛЬНОГО НАУЧНОГО ФОНДА ШОТА РУСТАВЕЛИ» YS2015.
Библиографический список
- Gagnidze, M. Iavich, G. Iashvili, Some Aspects of Post-Quantum Cryptosystems, Eurasian Journal of Business and Management, 5(1), 2017
- Gagnidze A.G., Iavich M.P., Iashvili G.U. Improved version of Merkle crypto system // Modern scientific researches and innovations. 2017. № 5 [Electronic journal]. URL: http://web.snauka.ru/issues/2017/05/81949
- Buchmann, J., Dahmen, E., Schneider, M.: Merkle tree traversal revisited. 2nd International Workshop on Post-Quantum Cryptography – PQCrypto 2008, LNCS 5299, pages 63–77. Springer, 2008.Dahmen, E., Okeya, K., Takagi, T., Vuillaume, C.: Digital
- Signatures out of Second-Preimage Resistant Hash Functions. 2nd International Workshop on Post-Quantum Cryptography – PQCrypto 2008, LNCS 5299, pages 109–123. Springer, 2008.
Количество просмотров публикации: Please wait