Введение
Если ссылаться на открытые источники информации, то определение «медицинская информативная система (МИС)» – это система автоматизации документооборота с целью лечебно-профилактических учреждений, в которой связаны система поддержки принятия медицинских решений, электронные медицинские карты о пациентах, сведения медицинских исследований в цифровой форме, данные мониторинга состояния пациента с медицинских приборов, средства общения между сотрудниками, финансовая и административная информация.
Используемые в настоящий момент в большинстве МИС, традиционные системы поддержки принятия решений, основанные на правилах, не способны обеспечить понимание «семантики» медицинских данных и клинических рекомендаций и на практике демонстрируют ряд существенных «ограничений».
На решение данных задач направлено создание интеллектуальной экспертной системы для персонифицированной медицинской диагностики, которая строиться на экспертных клинических рекомендациях и компьютерных средств представления знаний.
Основной целью проводимого исследования является разработка экспертной медицинской системы диагностики на базе нечеткой логики с целью обеспечение эффективной информационной поддержки процесса постановки диагноза, а также процесса рекомендательного оказания медицинской помощи.
Аналогичной ЭС медицинской диагностики, в которой применяют нечеткую логику, является наиболее известная диагностическая система MYCIN, предназначение которой заключается в наблюдении за состоянием больного при менингите и бактериальных инфекциях.
Начальная версия MYCIN была разработана в Стенфордском университете в 70 годах. На сегодняшний день эта система устанавливает заключение на уровне врача-специалиста. Она обладает расширенной базой знаний, вследствие чего способна применяться и в иных узконаправленных областях медицины
Актуальность создания данной информационной системы обусловлена необходимостью снижения вероятности ошибки в постановке диагноза, а также сокращением времени на постановку диагноза.
Для достижения поставленной цели решаются следующие задачи:
– построение модели предметной области;
– построение математической модели нечеткой логики;
– сбор знаний и накопление базы знаний;
– проектирование медицинской информационной системы;
– реализация экспертной системы.
Основные понятия нечеткой логики
Нечеткая логика является обобщением классической теории множеств и классической формальной логики. Данное понятие было впервые предложено американским ученым Лотфи Заде в 1965 г. Так же было введено понятие математической теории нечетких множеств как объекта с функцией принадлежности элемента к множеству, принимающей всевозможные значения в интервале [0; 1], а не только 0 или 1. На основе данного определения вводятся различные логические операции над нечёткими множествами и формулируется понятие лингвистической переменной, в качестве значений которой выступают нечёткие множества. Основным фактором возникновения новой теории стало наличие нечетких и приближенных рассуждений при описании человеком процессов, систем, объектов. Предметом нечёткой логики является исследование рассуждений в условиях нечёткости, размытости, сходных с рассуждениями в обычном смысле, и их использование в вычислительных системах.
Поскольку нечеткие множества описываются функциями принадлежности, а t-нормы и k-нормы обычными математическими операциями, можно представить нечеткие логические рассуждения в виде нейронной сети. Для этого функции принадлежности необходимо интерпретировать как функции активации нейронов, передачу сигналов как связи, а логические t-нормы и k-нормы, как специальные виды нейронов, выполняющие математические соответствующие операции. Имеется огромное разнообразие аналогичных нейро-нечетких сетей. К примеру, ANFIS (Adaptive Neuro fuzzy Inference System) – адаптивная нейро-нечеткая система вывода.
Она может быть описана в универсальной форме аппроксиматоров как:
помимо этого, данной формулой могут быть описаны также некоторые виды нейронных сетей, такие как радиально базисные сети (RBF) и многослойные персептроны (MLP).
Математическая модель нечеткой логики
Характеристикой нечеткого множества выступает функция принадлежности. Обозначим посредством MFc(x) степень принадлежности к нечеткому множеству C, которая представляет собой обобщение понятия характеристической функции обычного множества. Множество упорядоченных пар типа C={MFc(x)/x}, MFc(x)?[0,1] называется нечетким множеством С. Значение MFc(x)=0 означает отсутствие принадлежности к множеству, 1 – абсолютную принадлежность.
Рассмотрим на примере. Формализуем неточное определение «высокая температура (тела пациента)». В качестве X (область рассуждений) будет выступать шкала температуры в градусах Цельсия. Очевидно, она будет изменяться от 35 до 42 градусов. Нечеткое множество для определения «высокая температура (тела пациента)» может выглядеть следующим образом:
К примеру, температура тела 36,9 °C принадлежит ко множеству «Высокая» со степенью принадлежности 0,3. Для одного человека температура тела 36,9 °C может оказаться высокой, для другого – не слишком высокой. Именно в этом и проявляется нечеткость задания соответствующего множества.
Для нечетких множеств определены логические операции. Основными, необходимыми для расчетов, являются пересечение и объединение.
Пересечение двух нечетких множеств (нечеткое “И”):
Объединение двух нечетких множеств (нечеткое “ИЛИ”):
В теории нечетких множеств найден общий подход к использованию операторов пересечения, объединения и дополнения, осуществленный в треугольных нормах и конормах. Из рассмотренной выше реализации операций пересечения и объединения преобладают случаи t-нормы и t-конормы.
Для представления нечетких множеств даются понятия нечеткой и лингвистической переменных.
Нечеткая переменная отображается набором (N,X,A), где N – название переменной, X – универсальное множество (область рассуждений), A – нечеткое множество на X.
Нечёткие переменные могут являться значениями лингвистической переменной, которая находится на более высоком уровне в отличии от нечеткой переменной.
Любая лингвистическая переменная состоит из:
- названия;
- множества своих значений, которое также называется базовым терм-множеством T. Элементы базового терм-множества представляют собой названия нечетких переменных;
- универсального множества X;
- синтаксического правила G, по которому генерируются новые термы с применением слов естественного или формального языка;
- семантического правила P, которое каждому значению лингвистической переменной ставит в соответствие нечеткое подмножество множества X.
Проанализируем такое нечеткое понятие как «температура тела». Это и есть название лингвистической переменной. Сформируем для нее базовое терм-множество, которое будет состоять из трех нечетких переменных: «низкая», «нормальная» и «высокая» и установим область рассуждений в виде X= [35;42] (°C). Последнее, что осталось проделать – построить функции принадлежности для каждого лингвистического терма из базового терм-множества T.
Существует свыше десятка стандартных форм кривых для задания функций принадлежности. Наибольшее распространение приобрели: треугольная, трапецеидальная и гауссова функции принадлежности.
Треугольная функция принадлежности определяется тройкой чисел (a,b,c), и её значение в точке x вычисляется в соответствии с выражением:
.gif) (4)
(4)При (b-a)=(c-b) имеем случай симметричной треугольной функции принадлежности, которая может быть конкретно установлена двумя параметрами из тройки (a,b,c).
Аналогично для задания трапецеидальной функции принадлежности необходима четверка чисел (a,b,c,d):
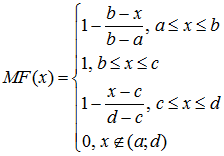 (5)
(5)При (b-a)=(d-c) трапецеидальная функция принадлежности принимает симметричный вид.
Функция принадлежности гауссова типа описывается формулой:
.gif) (6)
(6)и оперирует двумя параметрами. Параметр c обозначает центр нечеткого множества, а параметр у отвечает за крутизну функции.
Совокупность функций принадлежности для каждого терма из базового терм-множества T обычно изображаются вместе на одном графике. На рисунке 1 приведен пример описанной выше лингвистической переменной «температура тела».
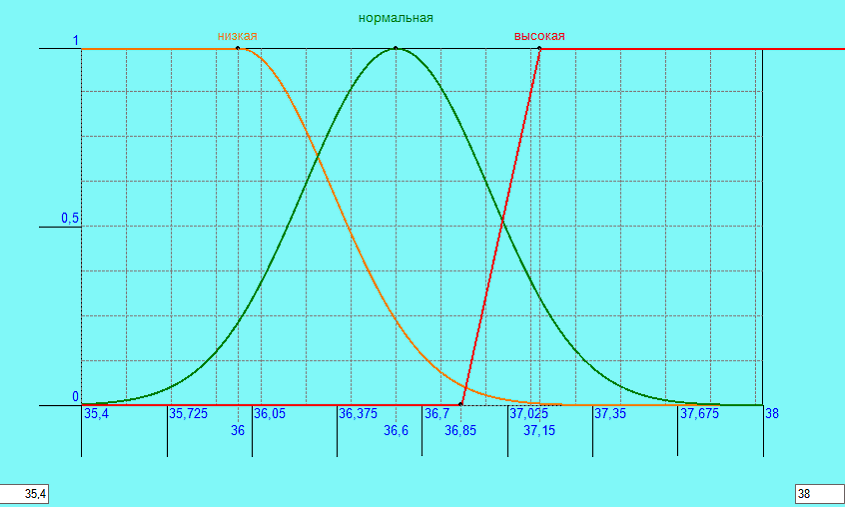
Рисунок 1 – Описание лингвистической переменной «температура тела»
Количество термов в лингвистической переменной редко превышает 7.
Нечеткий логический вывод
Основой для выполнения операции нечеткого логического вывода является база правил, включающая в себя нечеткие высказывания в форме «Если-то» и функции принадлежности для соответствующих лингвистических термов. При этом обязаны соблюдаться следующие условия:
1) Существует хотя бы одно правило для каждого лингвистического терма выходной переменной.
2) Для любого терма входной переменной имеется хотя бы одно правило, в котором этот терм используется в качестве предпосылки (левая часть правила).
В противном случае имеет место неполная база нечетких правил.
Пусть в базе правил имеется m правил вида:
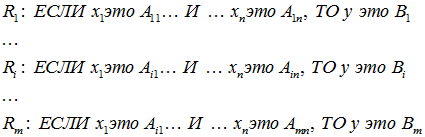
где xk , k=1..n – входные переменные; y – выходная переменная; Aik – заданные нечеткие множества с функциями принадлежности.
Результатом нечеткого вывода является четкое значение переменной y* на основе заданных четких значений xk , k=1..n.
В общем случае механизм логического вывода включает четыре этапа: введение нечеткости (фазификация), нечеткий вывод, композиция и приведение к четкости, или дефазификация. Общая схема приведена на рисунке 2.
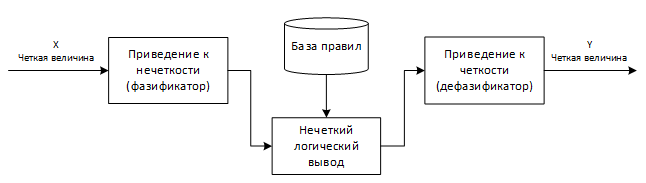
Алгоритмы нечеткого вывода различаются главным образом видом используемых правил, логических операций и разновидностью метода дефазификации. Разработаны модели нечеткого вывода Мамдани, Сугено, Ларсена, Цукамото.
Рассмотрим подробнее нечеткий вывод на примере механизма Мамдани. Это наиболее распространенный способ логического вывода в нечетких системах. В нем используется минимаксная композиция нечетких множеств. Данный механизм включает в себя следующую последовательность действий:
1) Процедура фазификации: определяются степени истинности, т.е. значения функций принадлежности для левых частей каждого правила (предпосылок или антецедентов). Для базы правил с m правилами обозначим степени истинности как Aik(xk), i=1..m, k=1..n.
2) Нечеткий вывод. Сначала определяются уровни «отсечения» для левой части каждого из правил:
Далее находятся «усеченные» функции принадлежности:
3) Композиция, или объединение полученных усеченных функций, для чего используется максимальная композиция нечетких множеств:
где MF(y) – функция принадлежности итогового нечеткого множества.
4) Дефазификация, или приведение к четкости. Существует несколько методов дефазификации. Например, метод среднего центра, или центроидный метод (формула (9)).
Геометрический смысл такого значения – центр тяжести для кривой MF(y). Рисунок 3 графически показывает процесс нечеткого вывода по Мамдани для двух входных переменных и двух нечетких правил R1 и R2.
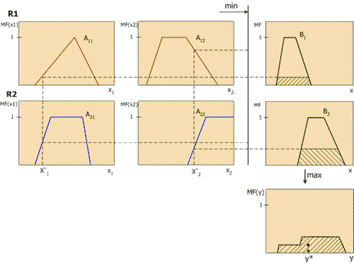
Рисунок 3 – Схема нечеткого вывода по Мамдани.
Проектирование экспертной системы
Выбор среды разработки ЭС для полноценного приложения, которое в дальнейшем сможет расти и развиваться – задача, требующая тщательного анализа всех достоинств и недостатков той или иной среды. Выбор СУБД так же представляет собой сложную задачу с множеством параметров и является одним из первостепенных этапов при разработке приложений баз данных. При выборе программного обеспечения необходимо учитывать финансовые затраты на приобретение необходимого оборудования, самой системы, разработку необходимого программного обеспечения на ее основе, а также обучение персонала с четом текущих и будущих потребностей конечных пользователей разрабатываемого продукта.
В конечном итоге средой разработки была выбрана IDE Microsoft Visual Studio 2017 Community, так как обладает огромными возможностями разработки ПО с бесплатной лицензией и гибкой библиотекой встроенный средств, инструментов и фреймоворков.
Языком программирования был выбран С# с использованием .Net Framework v.4.5.2 из-за своей гибкости и кроссплатформенности. Возможно, в дальнейшем появиться необходимость портирования разрабатываемого программного продукта на мобильные устройства, что в перспективе C# дает реализовать без особых проблем.
В качестве СУБД была выбрана MS SQL Server, так как уже встроена в инструментарий Visual Studio 2017 и позволяет проектировать программные продукты с поддержкой большого числа пользователей и создавать централизованное хранилище данных и знаний. Для работы с локальной копией БД используется SQLite.
Физическая модель базы данных, полученная с помощью CASE-средства ERwin Model Navigator r7.3, отображена на рисунке 4.
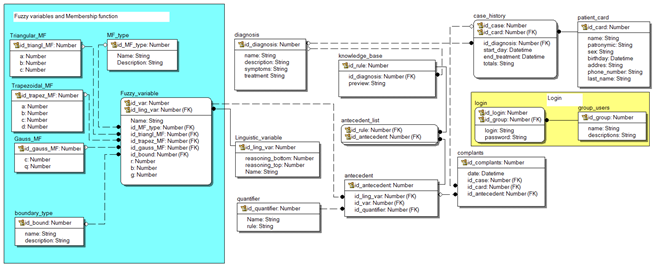
Рисунок 4 – Физическая модель базы данных
Весь back-end приложения реализован в классах, отображенных на рисунке 5. Данные классы представляют собой реализацию всех используемых алгоритмов и структур данных, не зависящих от конкретной ОС и экранных форм.

Рисунок 5 – Диаграмма классов в проекте приложения
Характеристика разработанного программного продукта
Программные продукты отличаются от привычных программ, которые не имеют определенного набора качественных характеристик, предопределяемых при формировании проектов, эти характеристики невозможно предварительно конкретизировать, т.к. функции обработки, обеспечиваемые программным средством, могут обладать разной глубиной проработки. Время и затраты на разработку программных продуктов не могут быть заранее точно спланированы.
Разработанный программный продукт МИС «Диагноз» на базе нечеткой логики можно отнести к категории алгоритмически сложных программных продуктов, так как основные вычислительные функции МИС имеют достаточно объемную и сложную математическую модель. Несмотря на сложную структуру, приложение обладает следующими качествами:
1) Надежность. Надежность функционирования программного продукта определяется работой без сбоев и стабильностью в работе программ, правильностью выполнения предписанных команд при обработке данных, возможностью диагностики возникающих ошибок в процессе работы приложения. Это качество позволило реализовать гибкая система обработки исключений, включенная в состав .Net Framework. Каждая непредвиденная программная ситуация сразу оповестит пользователя всплывающим сообщением о возможной ошибке.
2) Эффективность. Эффективность программного продукта рассматривается с позиций прямого его назначения – требований пользователя и с точки зрения расхода вычислительных ресурсов, необходимых для его эксплуатации. Несмотря на сложность решаемых задач приложением, оно потребляет относительно малое количество оперативной памяти и, за счет использования двойной буферизации прорисовки элементов управления, переносит часть вычислительных ресурсов на GPU.
3) Учет человеческого фактора означает обеспечение интуитивно понятного интерфейса для работы фактического пользователя, наличие вспомогательного действия при допущении ошибки или обучающего модуля в составе программного средства, хорошей технической документации для продуктивного применения пользователем заложенных в программном средстве функциональных возможностей, анализ и диагностику возникших ошибок и др. МИС разработана для диалогового взаимодействия с пользователем, интуитивно понятна и не отягощена различными элементами управления для настройки сложных взаимосвязей. Весь сложных функционал разбит на более мелкие и понятные и вынесен в отдельные диалоговые формы.
4) Модифицируемость программных продуктов представляет собой совокупность свойств, позволяющих вносить требуемые изменения: расширение функций обработки, переход на другую техническую базу обработки и др. МИС реализована таким образом, что с помощью инженера по знаниям, эксперты могут изменять, пополнять и удалять любые данные, включая те, которые расширяют функционал приложения. МИС обладает удобным редактором базы знаний, нечетких и лингвистических переменных, а также других данных, влияющих на диалоговые формы.
Системные требование для работы МИС «Диагноз» следующие:
– Процессор 300 MHz или выше;
– Оперативная память – 128 Мб RAM или выше;
– Видеоадаптер и монитор – SuperVGA (1024х720) или выше;
– Свободное место на HDD – 20 Мб или выше;
– клавиатура и мышь;
– Операционная система Windows XP / Vista / 7 / 8 / 8.1 / 10.
Экранные формы
При запуске МИС «Диагноз» открывается стартовое окно приложения. Экранная форма приведена на рисунке 6.
Приложение по умолчанию открывается из-под пользователя «Гость». Имя пользователя и режим, в котором работает приложение в данный момент отображаются в правом верхнем углу. Функционал приложения, учитывая права неавторизованного пользователя, ограничивает доступ к функциям редактирования данных и просмотра карт пациентов. Как видно из контекстного меню, доступны следующие пункты: Файл, консультация, сервис и помощь.
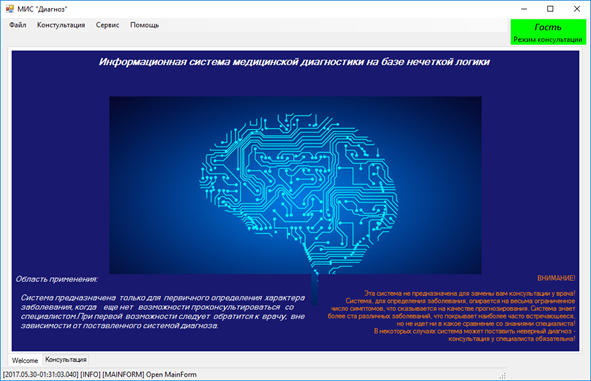
Рисунок 6 – Главная форма приложения МИС «Диагноз»
В пункте меню «Помощь» если выбрать подпункт «О программе…», то открывается экранная форма, которая изображена на рисунке 7.
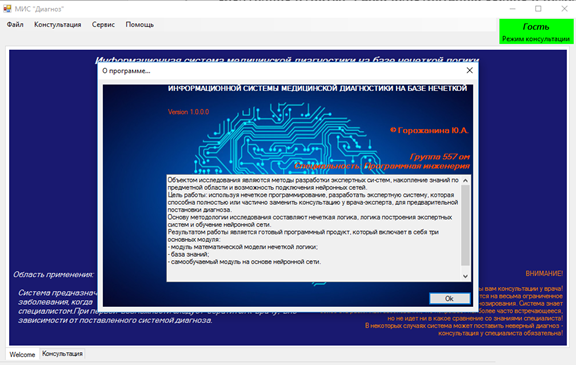
Рисунок 7 – О программе
Пункт меню «Сервис» включает в себя подпункты «Настройка приложения» и «Настройка пользователя». Причем для пользователя «Гость», второй пункт меню недоступен.
В пункте меню «Консультация» есть следующие подпункты: «Карта пациента» и «Диф.диагностика методом диалога с ЭС», причем «Карта пациента» так же недоступна из-за недостатка прав пользователя.
Если выбрать пункт меню «Диф.диагностика методом диалога» то на главной форме откроется вкладка «Консультация». Внешний вид экранной формы представлен на рисунке 8.
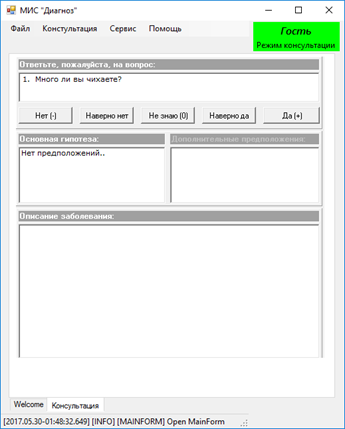
Рисунок 8 – Вкладка «Консультация»
Если начать отвечать на вопросы экспертной системы, то начнут формировать предположения о возможных диагнозах, которые МИС попробует подтвердить или опровергнуть, задавая дополнительные вопросы, опираясь на знания, занесенные экспертом и/или инженером по знаниям в базу знаний. Пример экранной формы в процессе консультации приведен на рисунке 9.
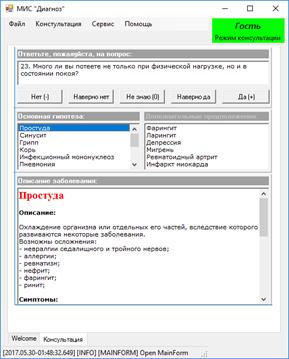
Рисунок 9 – Процесс консультации с ЭС
Чтобы сменить пользователя, необходима кликнуть на имени пользователя в правом верхнем углу формы и ввести логин и пароль. Процесс авторизации пользователя admin с паролем admin можно увидеть на рисунке 10.
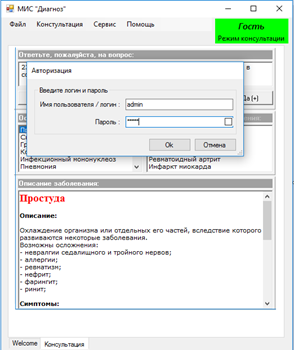
Рисунок 10 – Процесс авторизации администратора
После авторизации пользователя admin, в правом верхнем углу появиться надпись с именем пользователя и подписью «Полный доступ», а также измениться цвет кнопки на красный, что означает, что текущий пользователь имеет полный набор прав и имеет доступ ко всем функциям приложения. Например, пользователи из группы администраторов могут добавлять, изменять и удалять других пользователей системы. На рисунке 14 изображено окно редактирования пользователя.
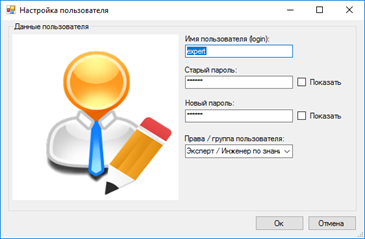
Рисунок 11 – Редактирование пользователя Expert
На рисунке 12 показан раздел администрирования – управление пользователями.
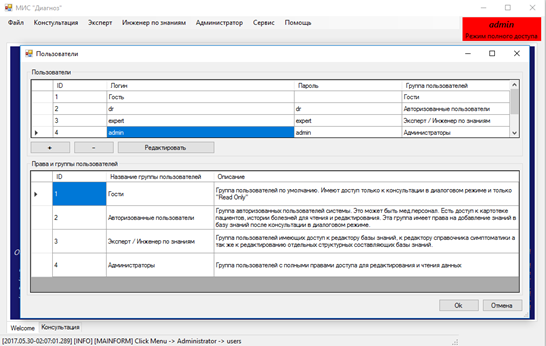
Рисунок 12 – Администрирование и управление пользователями
Различные редакторы для добавления ключевых данных представлены на рисунке 13.
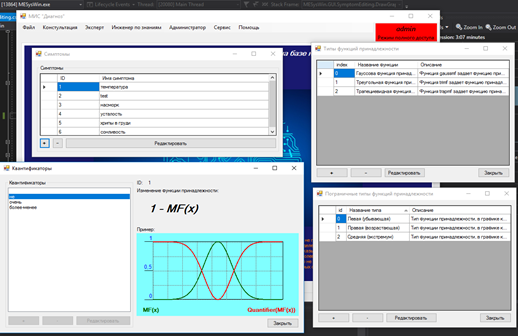
Рисунок 13 – Различные редакторы данных информационной системы
Редактор симптомов с отображением термов на графике представлен на рисунке 14.
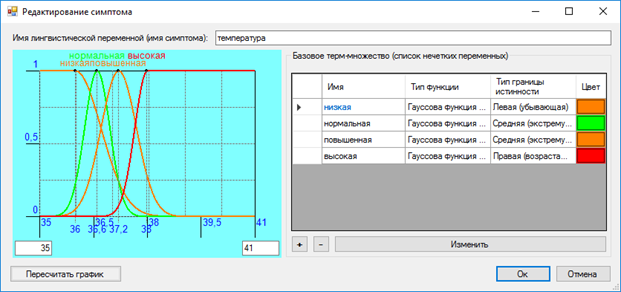
Рисунок 14 – Редактор лингвистических переменных нечеткой логики
Заключение
В процессе работы были собраны и изучены материалы согласно вопросам, связанным с проведением диагностики различных заболеваний, а также были изучены способы проектирования и реализации экспертных систем на базе нечеткой логики.
Среди методов организации экспертных систем были рассмотрены ключевые направления с позиции достоинств и недостатков, и наиболее оптимальной была подобрана структура с использованием нечетких множеств и правил на их основе. Благодаря тому, что на сегодняшний день структура логических рассуждений медицинских работников-диагностов аналогична структуре систем с нечеткой логикой, система дает возможность отвлечься от конкретных значений замеров, и тем самым исключить повторения правил. Это позволило существенно сократить объём базы знаний и повысить темп работы программного продукта.
После консультации с медиками-диагностами было также принято решение о внедрении в пользовательский интерфейс справочной системы. Это руководство ориентировано на упрощение принятия окончательного решения лично врачом-диагностом уже после получения списка предполагаемых диагнозов.
Также было реализовано объединение с интеллектуальными парадигмами для обучения экспертной системы способом машинного обучения с применением нейронных сетей Хопфилда.
Результатом работы является медицинская информационная система «Диагноз», которая дает возможность посодействовать медицинским работникам разных направлений и квалификаций в постановке диагноза пациентам.
Библиографический список
- Штовба С. Д. Введение в теорию нечетких множеств и нечеткую логику. – Винница: УНИВЕРСУМ-Винница, 2001. – 756 с..
- Паклин Н. А. Нечеткая логика — математические основы [Электронный ресурс] URL: https://basegroup.ru/print/228 (Дата обращения 05.06.2017)
- Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений. – М.: Мир, 1976.
- Круглов В.В., Дли М.И. Интеллектуальные информационные системы: компьютерная поддержка систем нечеткой логики и нечеткого вывода. – М.: Физматлит, 2002.
- Леоленков А.В. Нечеткое моделирование в среде MATLAB и fuzzyTECH. – СПб., 2003.
- Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы. – М., 2004.
- Масалович А. Нечеткая логика в бизнесе и финансах. [Электронный ресурс] URL: http://www.tora-centre.ru/library/fuzzy/fuzzy-.htm (Дата обращения 05.06.2017)
- Kosko B. Fuzzy systems as universal approximators // IEEE Transactions on Computers, vol. 43, No. 11, November 1994. – P. 1329-1333.
- Cordon O., Herrera F., A General study on genetic fuzzy systems // Genetic Algorithms in engineering and computer science, 1995. – P. 33-57.
