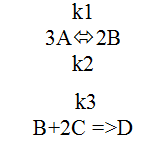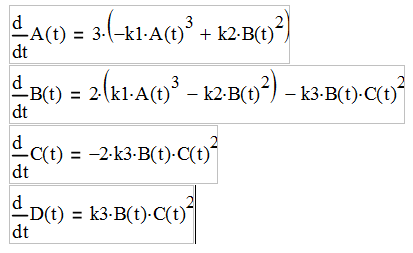Введение
Кинетика является одним из важнейших разделов физической химии и химической технологии. Умение правильного применения ее законов является атрибутом каждого профессионального химика-исследователя и химика-технолога. В данной статье представлена методика исследования кинетики сложных химических процессов, а именно подбор констант скорости кинетических уравнений для выбранного механизма и способ оценки полученного решения с использованием искусственной обучаемой нейронной сети.
Исходными данными для решения поставленной задачи являются экспериментально полученные данные зависимости концентрации всех химических компонентов системы от времени, т.е. кинетические кривые. На основе предполагаемого механизма получают систему дифференциальных уравнений формальной кинетики, в которой неизвестными величинами являются константы скорости прямых и обратных реакций для обратимых процессов и константа скорости для необратимых стадий. После определения констант скоростей (обычно методом подбора) результат моделирования оценивают по расхождению расчётных значений с экспериментальными стандартными статистическими методами. Если модель оказывается неадекватной (по критерию Фишера, например) или в упращённом варианте относительная погрешность расчётных результатов превышает допустимую, то можно утверждать, что предложенный механизм является неверным и попытаться подобрать другой.
Основной проблемой простого перебора значений констант скоростей реакций является то, что такая методика хорошо работает только для очень простых механизмов в 1-2 реакции. Для большего числа реакций такой метод требует слишком много времени даже с использованием компьютерной техники. Известная “задача коммивояжёра” [1] является примером подобной проблемы. При этом использование вычислительных методов нейронных сетей или генетических алгоритмов позволяет решать её на хорошем уровне при существенно меньшем использовании компьютерных ресурсов.
В данной работе представлено решение на основе обучаемой нейронной сети в среде NeuralNetwork Toolbox программы Matlab [2]. Для отработки методики используется расчётная модель процесса в среде MathCad, что позволяет быстро оценить качество предлагаемого метода, поскольку константы скоростей точно известны (заданы нами), но не известны обученной нейронной сети. Для передачи данных для обучения между указанными программами использовался Excel.
Подготовка данных для обучения нейронной сети
Для примера рассмотрим механизм простого процесса с одной обратимой реакцией (k1 – константа прямой реакции, k2 – константа обратной) и одной необратимой (константа k3):
В этом случае мы получаем следующую систему дифференциальных уравнений:
На основе этой модели получаем данные (зависимости концентраций компонентов от времени) для обучения нейронной сети, варьируя значениями констант k1, k2 и k3. Следует учесть, что чем больше возможных вариантов значений констант и меньше интервал изменения значения времени, тем выше точность полученных значений в итоге (и больше массив исходных данных). На данном этапе удобным инструментом реализации задачи оказалась функция Odesolve в среде MathCad (см. листинг), которая позволяет решить систему дифференциальных уравнений.
Рисунок 1. Решение системы дифуравнений в среде MathCad
Далее формируется таблица кинетических данных в листе Excel (см. таблицу 1). Для упрощения генерации исходных данных приняли значение второй константы равное 1/k1.
Важная деталь: начальные условия, а именно данные которые соответствуют нулевому моменту времени (tau), следует исключить из массива, поскольку эта группа данных будет иметь противоречивый смысл для нейронной сети, что приведет к увеличению погрешности в начале интервала времени. При этом концентрации всех компонентов в начальный момент времени и так всегда известны.
Обучение и использование нейронной сети
Следующим шагом импортируем данные в Matlab (R2015a, 32 разрядная версия) в виде матриц, разделяя их на 2 массива: «Inputs» и «Targets». В первый массив входят время и концентрации, во второй константы. Подробное видео об использовании Matlab в этой части представлено в [3].
Далее необходимо активировать NeuralNetworkToolbox при помощи функции «nnstart». В последующем необходимо выбрать массивы данных для тренировки, разделить массив данных на тренировочный, валидационный и тестовый (процентные значения этих категорий можно оставить по умолчанию). Тренировочное множество – данные, на которых нейронная сеть тренируется. Валидационное множество – данные, которые используются для улучшения обобщающей способности сети, а также для остановки процесса обучения если обобщающая способность перестает улучшаться. Тестовое множество – данные, которые не участвуют в процессе обучения, а используются для проверки работы сети после ее обучения.
Далее выбираем количество нейронов в скрытом слое. Чем больше нейронов, тем более точный результат будет генерировать нейронная сеть с одновременным увеличением времени на обучение. Однако в некоторых случаях не следует выбирать слишком много, особенно в случае не идеальных моделей или данных, так как это приведет к образованию полиномов и поверхностей более высокого порядка, которые могут неверно охарактеризовать реальный процесс.
После обучения (при необходимости, проверки) нейронную сеть можно использовать. Искусственная нейронная сеть показывает хорошую точность в пределах тренировочных данных и на небольшом участке за их пределами.
В данном примере обучение искусственной нейронной сети осуществлялось при условиях:
k1=(0.2; 0.4; 0.6; 0.8; 1; 1.5; 2)
k3=(0.2; 0.4; 0.5; 0.6; 0.8; 1; 1.5; 2)
k2=1/k1
Таблица 1 – Фрагмент тренировочного массива
|
k1 |
k3 |
tau |
Ca |
Cb |
Cc |
Cd |
|
0,20 |
0,80 |
4,30 |
0,60 |
0,07 |
0,94 |
3,53 |
|
0,20 |
0,80 |
4,40 |
0,60 |
0,07 |
0,93 |
3,54 |
|
0,20 |
0,80 |
4,60 |
0,58 |
0,07 |
0,91 |
3,55 |
|
0,20 |
0,80 |
4,70 |
0,58 |
0,07 |
0,90 |
3,55 |
|
0,20 |
0,80 |
4,80 |
0,57 |
0,07 |
0,89 |
3,55 |
|
0,20 |
0,80 |
4,90 |
0,57 |
0,06 |
0,89 |
3,56 |
|
0,20 |
0,80 |
5,00 |
0,56 |
0,06 |
0,88 |
3,56 |
|
0,20 |
1,00 |
0,10 |
2,77 |
0,41 |
4,51 |
1,74 |
|
0,20 |
1,00 |
0,20 |
2,11 |
0,30 |
3,43 |
2,29 |
|
0,20 |
1,00 |
0,30 |
1,79 |
0,25 |
2,88 |
2,56 |
|
0,20 |
1,00 |
0,40 |
1,58 |
0,22 |
2,54 |
2,73 |
|
0,20 |
1,00 |
0,60 |
1,33 |
0,18 |
2,13 |
2,94 |
|
0,20 |
1,00 |
0,70 |
1,25 |
0,16 |
1,98 |
3,01 |
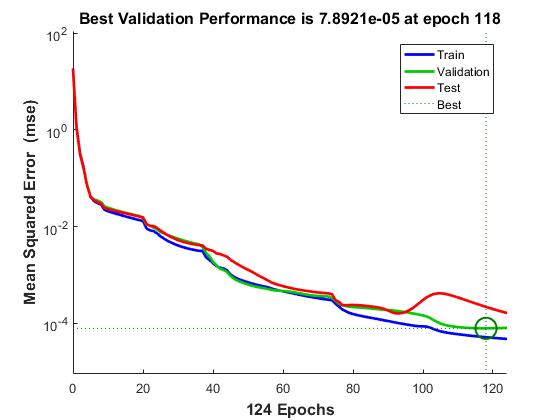
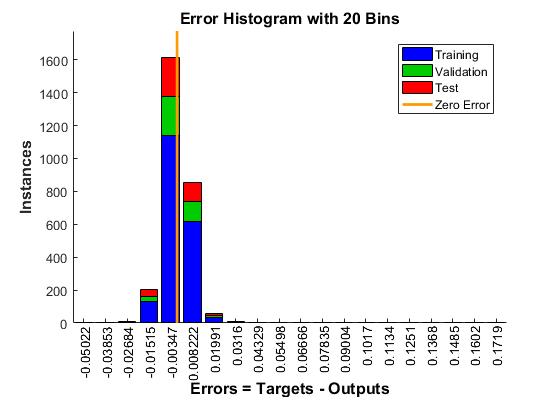
После обучения нейронной сети можно ознакомиться с характеристиками ее обучения, такими как: график обучения (рис. 2), гистограмма ошибок (рис. 3), диаграммы обобщающей способности (рис. 4), графиками изменения градиента, изменения ошибки и валидации.
Рисунок 2. График обучения нейронной сети
Рисунок 3. Гистограмма ошибок
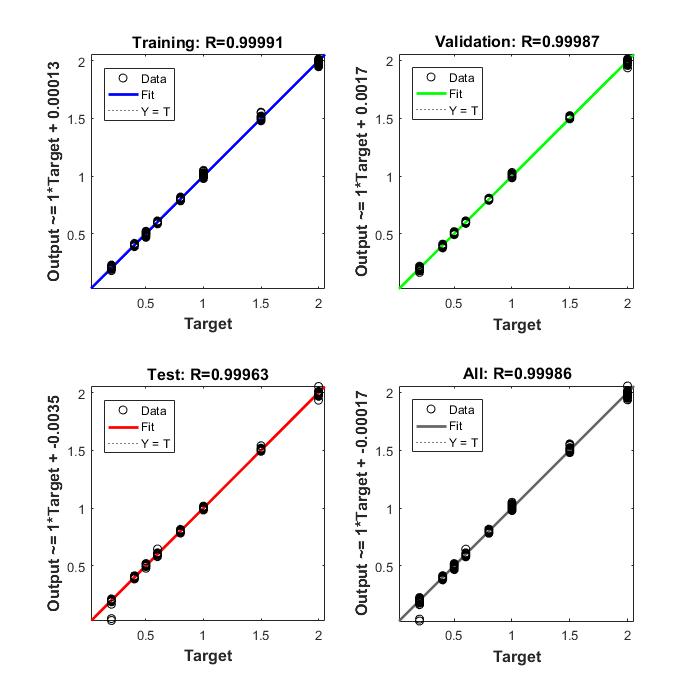
Рисунок 4. Диаграммы обобщающей способности сети
Использование обученной нейронной сети
Использование обученной сети заключается в обработке ею исходных кинетических данных (экспериментальных или расчётных как в нашем случае) и подборе констант скоростей, при которых определённые нею значения обеспечат минимально возможное расхождение исходной зависимости концентраций компонентов от времени с расчётной.
Для получения исходной кинетической зависимости использовали модель в Mathcad (система дифуравнений) с коэффициентами констант реакций k1=1,7 и k3=1,3. Был получен массив кинетических данных (табл. 2).
Таблица 2 – кинетические данные при k1=1,7 и k3=1,3
|
tau |
Ca |
Cb |
Cc |
Cd |
|
0,00 |
6,00 |
0,00 |
8,00 |
0,00 |
|
0,10 |
3,24 |
0,94 |
6,20 |
0,90 |
|
0,20 |
2,73 |
0,75 |
5,13 |
1,43 |
|
0,30 |
2,42 |
0,64 |
4,50 |
1,75 |
|
0,40 |
2,21 |
0,56 |
4,06 |
1,97 |
|
0,50 |
2,05 |
0,50 |
3,74 |
2,13 |
|
0,60 |
1,93 |
0,46 |
3,49 |
2,26 |
|
0,70 |
1,83 |
0,43 |
3,29 |
2,36 |
|
0,80 |
1,74 |
0,40 |
3,12 |
2,44 |
|
0,90 |
1,67 |
0,38 |
2,98 |
2,51 |
|
1,00 |
1,61 |
0,36 |
2,85 |
2,57 |
Для использования обученной сети в Matlab необходимо в командном окне воспользоваться командой sim(net,[tau;Ca;Cb;Cc;Cd]), подставляя соответствующие символам значения. Следует обратить внимание, что нейронная сеть в любом случае попытается выдать ответ, поэтому проверка модели по одной точке недостаточна. Для работы следует использовать определенную методику оценки точности, такую как среднеквадратичное отклонение.
С помощью указанной команды sim было введено 6 зависимостей концентрации от времени и получены расчётные константы скоростей. Усреднённые значения констант: k1=1,6943 (исходная 1,7), k3=1,3106 (исходная 1,3). Относительная погрешность для расчётных значений констант составила 0,3% для k1 и 0,8% для k3.
Существенно, что для всех 6-ти проверочных точек значения констант также были очень близки на том же уровне относительной погрешности. При использовании обученной нейронной сети по иному механизму (с другой системой дифуравнений) полученные значения констант в каждой из точек существенно (100% и больше) отличались бы друг от друга. Именно этот факт позволяет рассматривать предложенное решение как основу для широкого применения данной методики в практике химиков-кинетиков.
Естественно, что следующим шагом будет реализация методики в одной программной среде такой как Matlab или любой другой, поддерживающей обучаемые нейронные сети: SciLab (бесплатный аналог Matlab), Python и другие.
Библиографический список
- Задача коммивояжёра [электронный ресурс]. Режим доступа - https://ru.wikipedia.org/wiki/Задача_коммивояжёра
- Neural Network Toolbox Examples [электронный ресурс]. Режим доступа - https://www.mathworks.com/help/nnet/examples.html
- Обучение и использование нейронной сети для определения констант скоростей сложных химических процессов[электронный ресурс]. Режим доступа – https://www.youtube.com/watch?v=2afTCq1IWNc&t=1s
Количество просмотров публикации: Please wait