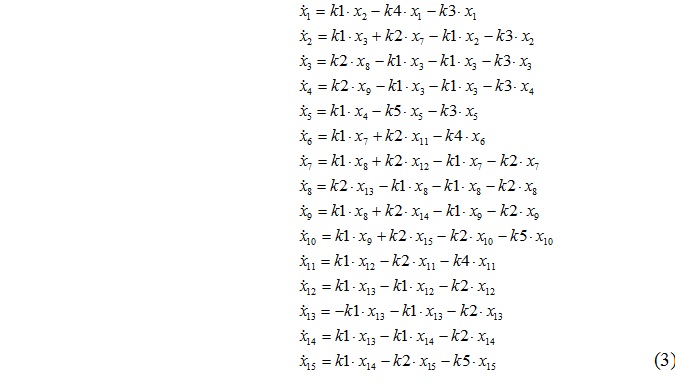Рулоны сена с внесенным консервантом после формирования в пресс-подборщике обматываются шпагатом и сбрасываются на землю. Далее рулоны подбираются и транспортируются на хранение. В хранилище рулоны размещаются таким образом, чтобы они были подвержены воздействию воздушных масс, при котором из рулона выводятся излишки влаги совместно с ведённым консервантом.
Для исследования процесса удаления влаги при естественной вентиляции рулона рассмотрим следующую модель процесса.
Сделаем следующие допущения:
1. В процессе хранения рулон лежит на боку на влаго- изолирующем основании и с нижней его части влагоотдача отсутствует.
2. Выделим из центральной части рулона некоторую прямоугольную пластину толщиной ![]() .
.
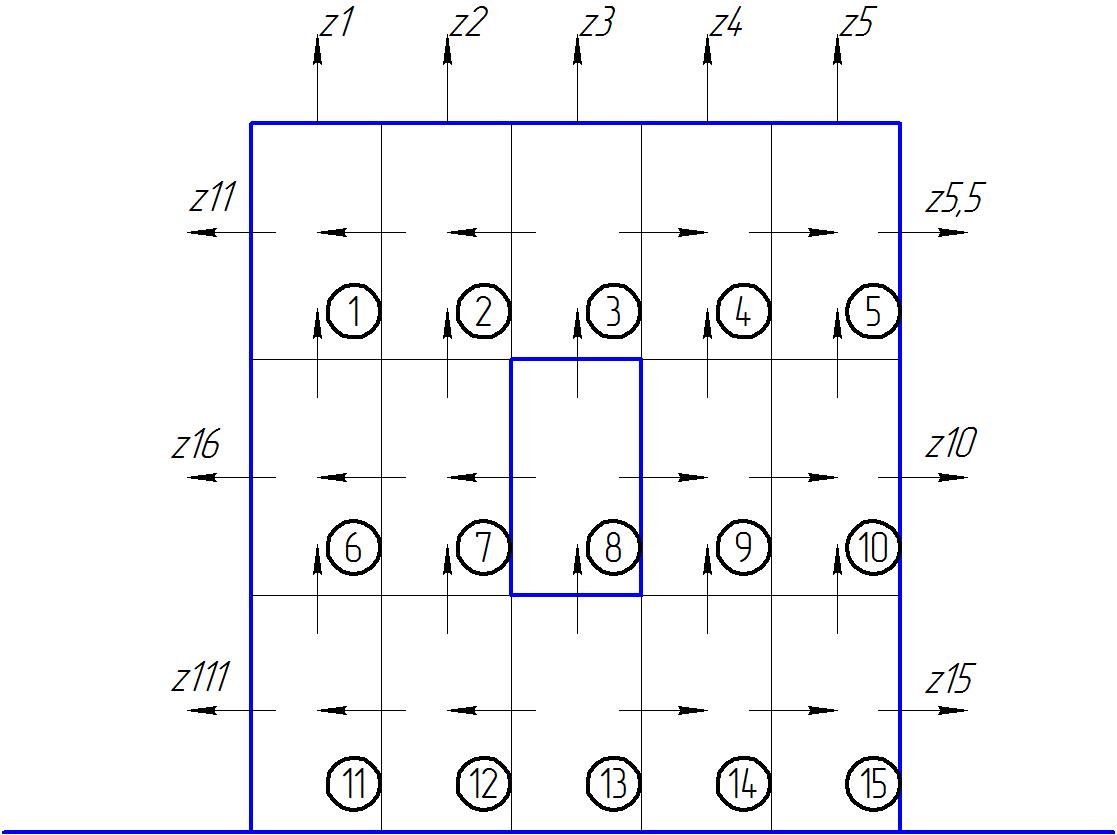
3. Разобьём пластину на некоторое (нечётное) количество прямоугольников, между которыми осуществляется влаго- массо- обмен, рисунок 1.
4. Считаем, что влажность травы по всей пластине одинаковая и составляет ![]() ,
,
концентрация консерванта так же по всей пластине одинаковая и составляет ![]()
5. Выход влаги и консерванта из рулона происходит прямо-пропорционально в зависимости от внешних условий с верхней грани и боковых, правой и левой граней.
6. Выходные векторы влаги и консерванта с верхней грани (z1, z2, z3, z4, z5) отличаются от векторов выхода влаги и консерванта с торцов (z11, z6, z111 и z55, z10, z15), рисунок 1.
7. При удалении влаги с верхней грани и торцов пластины внутри пластины происходит перемещение влаги по некоторым векторам, представленным на рисунке 1.
Вектор со стрелкой направленной внутрь квадрата принимается со знаком (+), а выходящий из квадрата – со знаком (- ).
8. Процесс удаления влаги протекает некоторое время, после которого в рулоне устанавливается равновесное влагосодержание и отсутствует консервант.
9. Так как изменение содержания влаги и консерванта происходит по времени, то состояние всей системы описывается системой дифференциальных уравнений.
Разработка математической модели
Для составления системы дифференциальных уравнений используем схему, представленную на рисунке 1, с учетом знаков направления стрелок движения влаги в рулоне.
Рисунок 1. Схема векторов движения влаги и консерванта в элементарной пластине.
Введем следующие обозначения коэффициентов перемещения влаги внутри рулона и испарения с поверхности:
k1 – вектор перемещения влаги внутри рулона по горизонтали;
k2 – вектор перемещения влаги внутри рулона по вертикали;
k3 – вектор удаления влаги с верхней части рулона;
k4 – вектор удаления влаги с левого торца рулона;
k5 – вектор удаления влаги с правого торца рулона.
С учётом принятых обозначений, уравнение изменения концентрации влаги и консерванта в первом прямоугольнике имеет вид:
Аналогично для второго прямоугольника изменения концентрации влаги и консерванта уравнение имеет вид:
Разработанная система уравнений изменения концентрации влаги и консерванта для всех ячеек пластины имеет вид:
Анализ математической модели
Для проверки и анализа разработанной математической модели необходимо выполнить её решение некоторых априорно заданных условий. Реальное распределение потоков внутри и с поверхности рулона может быть получено после практического определения коэффициентов k1 – k5 в реальных условиях сушки рулона.
Для решения системы (1) необходимо задать начальные условия.
Примем для всех переменных начальное условие равное единице [1]:
Тогда решение системы (3) будет в условных единицах, и изменяться от 1,0 – при начальной влажности рулона, до 0 – при конечной влажности рулона.
Примем также, что воздушный поток, омывающий рулон движется с права на лево, т.е. левая часть является наветренной, а правая – подветренной.
Коэффициенты отдачи влаги приняты равными [2]:
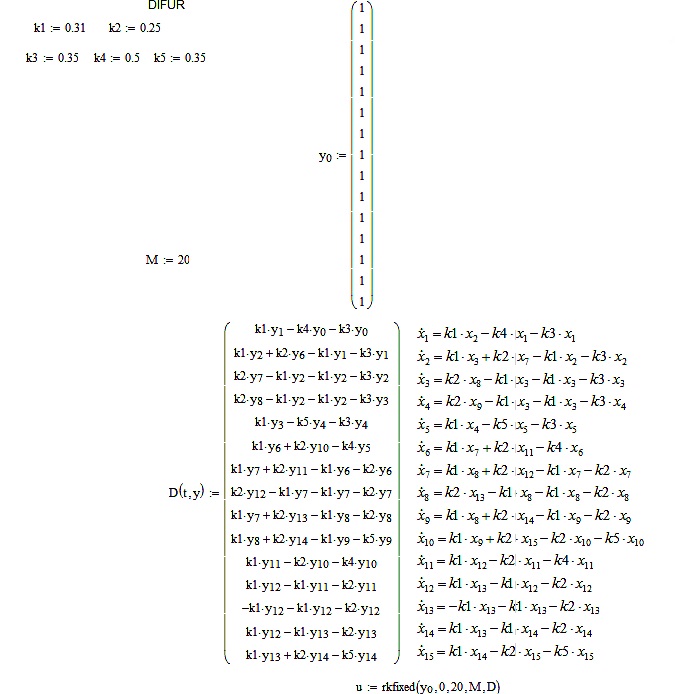
Для решения задачи (2) – (5) в системе MathCAD разработана программа, рисунок. 2.
Рисунок 2 Программа решения задачи (2) – (5) в системе MathCAD
Решение задачи в графическом виде приведено ниже на рисунке 3 – 7.
На рисунке 3 приведены кривые изменения концентрации влажности по всем квадратам пластины. Как видно изменения происходят во всех ячейках, на рисунке 3 приведены все пятнадцать кривых, что затрудняет их сравнение и анализ.
Рис. 3 Кривые изменения всех переменных решения системы уравнений
Для упрощения сравнительного анализа разобьём решения и рассмотрим их в следующей последовательности:
- Изменение влажности верхних ячеек прямоугольника
- Изменение влажности ячеек левой и праовой торцевых ячеек.
- Изменение влажности внутренних ячеек прямоугольника
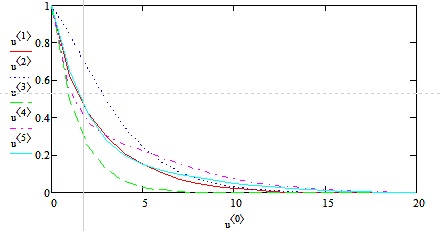 Рисунок 4 Кривые изменения влажности верхних ячеек прямоугольника
Рисунок 4 Кривые изменения влажности верхних ячеек прямоугольника
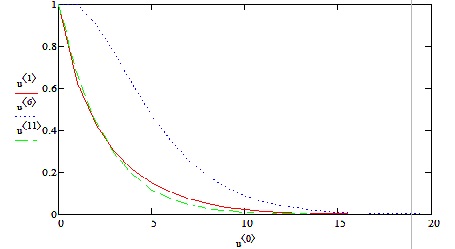
На рисунке 4 приведены изменение влажности верхних ячеек прямоугольника. Как видно изменение влажности происходит во всех ячейках примерно одинаково, и процесс сушки заканчивается в одно и то же время.
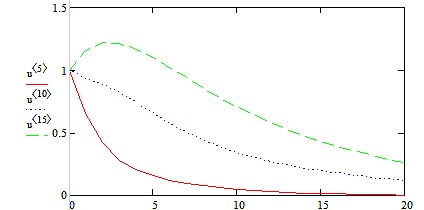
Рисунок 5 Кривые изменения влажности верхних левого торца прямоугольника
На рисунке 5 приведены изменение влажности ячеек левого торца прямоугольника. Как видно изменение влажности происходит в первой и одиннадцатой ячейках примерно одинаково, а в шестой ячейке сушка идёт, по сравнению с первыми двумя медленнее.
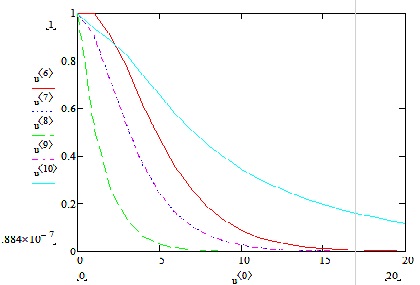
Рисунок 6 Кривые изменения влажности верхних правого торца прямоугольника
На рисунке 6 приведены изменение влажности ячеек правого торца прямоугольника. Как видно изменение влажности происходит по разному. Быстрее всех сохнет пятая ячейка, процесс сушки десятой ячейки происходит гораздо медленнее. А в пятнадцатой ячейке в начальный момент происходит даже увеличение количества влаги и далее только начинается процесс сушки. Полное высыхание ячеек происходит в разное время и дольше всех сохнет пятнадцатая ячейка.
Рисунок 7 Кривые изменения влажности ячеек среднего ряда прямоугольника
На рисунке 7 приведены изменение влажности ячеек среднего ряда прямоугольника. Как видно изменение влажности происходит по разному. Быстрее всех сохнет восьмая ячейка, седьмая и восьмая ячейки сохнут примерно одинаково, процесс сушки десятой ячейки происходит гораздо медленнее и не заканчивается за время решения задачи.
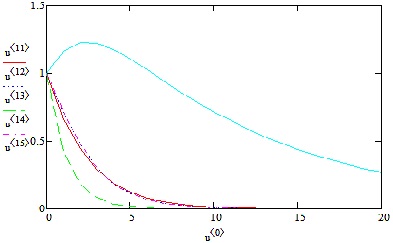
Рисунок 8 Кривые изменения влажности ячеек нижнего ряда прямоугольника
На рисунке 8 приведены изменение влажности ячеек нижнего ряда прямоугольника. Как видно здесь так же изменение влажности происходит по разному.
Быстрее всех сохнет тринадцатая ячейка, одиннадцатая и двенадцатая ячейки сохнут одинаково, процесс сушки пятнадцатой ячейки происходит гораздо медленнее и не заканчивается за время решения задачи.
Библиографический список
- Валге А.М. Использование информационных технологий при проектировании процессов производства продукции растениеводства А.М. Валге, Э.А. Папушин, Е.Г. Пакскина//Механизация и электрификация сельского хозяйства. 2012. № 3. С. 17-18.
- Валге А.М. Модель процесса досушивания измельченного сена активным вентилированием /Валге А.М., Добринов А.В.//Технологии и технические средства механизированного производства продукции растениеводства и животноводства. 2003. № 75. С. 26-33.
Количество просмотров публикации: Please wait