Введение
К наиболее часто применяемым методам прогнозирования относятся методы эконометрики и анализа временных рядов [1, 2]. В последнее время развиваются также новые направления, основанные, например, на формализме нечеткой логики [3, 4].
Среди моделей анализа временных рядов особое место занимают адаптивные модели, к которым относятся самонастраивающиеся рекуррентные модели, отражающие динамические свойства исследуемого временного ряда. Различная информационная ценность предшествующих значений (уровней) временного ряда учитывается различными весовыми коэффициентами.
Все адаптивные модели делятся на два класса: модели скользящего среднего (СС-модели) и авторегрессии (АР-модели). Согласно схеме скользящего среднего оценкой текущего уровня является взвешенное среднее всех предшествующих уровней, при этом вес (множитель) отражает информационную ценность наблюдения: вес тем больше, чем ближе наблюдение находится к текущему уровню. Такие модели хорошо подходят для процессов с трендом, но не позволяют отражать, например, сезонные колебания. Частным случаем СС-моделей является модель экспоненциального сглаживания (модель Брауна).
В СС-моделях моделирование производится с помощью параметра сглаживания, который принимает значения в интервале от 0 до 1. Параметр сглаживания принимает значение больше 0,5 для быстроизменяющихся процессов и меньше 0,5 для относительно стабильных процессов. Подбор подходящего значения данного параметра представляет определенные трудности при практическом использовании данного класса моделей.
В настоящей работе рассмотрена методика построения модели Брауна и подбор параметра модели с использованием доступного и легального программного обеспечения. Предлагаемый алгоритм может быть использован и для других адаптивных моделей, например, модели Хольта-Уинтерса.

Математическое описание модели

При построении линейной модели Брауна можно выделить следующие этапы:

1. По нескольким первым точкам временного ряда строим линейную модель:

y_th(t) = a₀ + a₁t .

Значения параметров линейной модели оцениваются с помощью метода наименьших квадратов.

2. С использованием найденных на предыдущем этапе параметров a₀ и a₁ находим прогноз на шаг вперед (т.е. для t = 1):

y₁ = a₀₍₀₎ + a₁₍₀₎t = a₀₍₀₎ + a_{1(0) .}

3. Находим величину e отклонения фактического значения экономического показателя от расчетного:

e = y(t) – y_th(t) . (1)

4. Корректируем параметры модели по формулам:

a_0(t) = a_0(t-1) + a_1(t-1) + (1 – b²)Чe(t) , (2)

a_1(t) = a_1(t-1) + (1 – b)²Чe(t) , (3)

где b = 1 – a, a – параметр сглаживания.

5. С помощью скорректированных на предыдущем шаге параметров находим прогноз на следующий момент времени (t = 1):

y_th(t) = a_0(t) + a_1(t)t . (4)

Точечный прогноз на будущее рассчитывается по формуле

y_th(n + t) = a_0(n) + a_1(n)t , t = 1, 2, … (5)

Здесь n – число наблюдений.

Компьютерная реализация модели

Рассмотрим построение модели Брауна данным [1] из табл.1.
Табл. 1. Исходные данные для построения модели Брауна

t	y	t	y	t	y
1	27,3	14	193,5	27	400,6
2	41,8	15	207,4	28	409,4
3	42,8	16	221,2	29	426
4	56,2	17	267,2	30	402
5	72,5	18	264	31	398,7
6	56	19	273,8	32	418,1
7	70	20	321	33	424,6
8	74,9	21	317,4	34	435,1
9	103,3	22	342	35	439,8
10	111,3	23	350,6
11	125,2	24	368,5
12	189,3	25	397
13	169,1	26	382,9

При проведении вычислений удобно использовать сочетание нескольких программных продуктов. На первом этапе построение модели линейной регрессии удобно выполнить в электронных таблицах Excel.
В электронных таблицах Excel введем в столбец исходные данные, добавим в таблицу нулевую строку и вычислим параметры a₀ (функция ОТРЕЗОК) иa₁ (функция НАКЛОН) по первым пяти точкам. Вычисление параметра a₀ показано на рис. 1. Вычисление параметра a₁ выполняется аналогично с помощью функции НАКЛОН. 
После построения модельных значений для всех исходных точек вычисляем прогнозные значения по формуле (5).

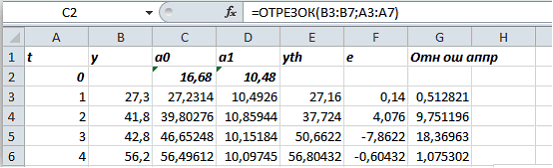
Рис. 1. Вычисление параметра a₀

Полностью вычисления по модели Брауна в электронных таблицах удобно выполнять при известном фиксированном значении параметра a. Как правило, значение этого параметра неизвестно и в распоряжении экономиста имеется только набор значений y. Тогда для определения параметра aможно использовать следующий алгоритм. Разобьем отрезок [0; 1] на n равных частей. Обозначим точки разбиения как a₀ , a₁ , a₂ , … , a_n (a₀ = 0, a_n= 1). Для каждого значения a_i , i = 1, … , n, выполним вычисления модельных значений y_th . Для характеристики точности вычислений удобно использовать функционал ошибки
 .
По результатам вычислений в качестве параметра a выбираем значение, соответствующее минимуму функционала ошибки.

На рис. 2 показан график исходных и модельных значений.

Реализацию алгоритма подбора параметра удобно проводить с помощью пакетов прикладных программ, например, свободно распространяемого пакета Scilab [5]. 
Аналогичный подход можно применить для подбора параметров в более сложной модели Хольта-Уинтерса [2].

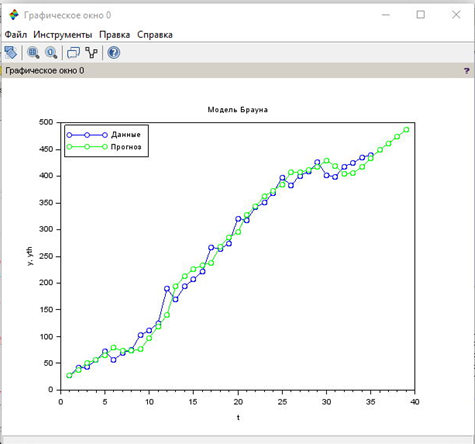
Рис. 2. Исходные и модельные значения в модели Брауна

Проверка точности модели
Для оценки точности модели вычислим среднюю относительную ошибку аппроксимации. Считается, что точность модели хорошая, если среднее значение относительной погрешности не превышает 5% , удовлетворительная, если среднее значение относительной погрешности не превышает 15%, и неудовлетворительная, если среднее значение относительной погрешности больше 15%.
Для каждого отдельного значения y относительная ошибка аппроксимации вычисляется по формуле (y_i - y_th,i)/y_i , i = 1, … , n. Здесь y_th,i – значение y, соответствующее модели. Средняя относительная ошибка аппроксимации получается как среднее всех относительных ошибок. 
Для рассмотренного примера получим значение 6,75. Таким образом, точность модели является хорошей.

Выводы

В данной работе детально описан алгоритм компьютерной реализации модели Брауна и подбора параметров модели. Проведенные вычисления показали хорошее соответствие с имеющимися в литературе данными.

1. Экономико-математические методы и прикладные модели: учебник для бакалавров / В.В. Федосеев, А.Н. Гармаш, И.В. Орлова. – М.:Юрайт, 2012. – 328 с.
2. Семененко М.Г., Унтилова Л.А. Модель Хольта-Уинтерса: математические аспекты и компьютерная реализация // Вектор науки Тольяттинского государственного университета. Серия: Экономика и управление. 2016. № 3 (26). С. 64-67.
3. Кулакова Н.Н., Семененко М.Г., Черняев С.И., Унтилова Л.А. Анализ финансовой устойчивости предприятия // Вектор науки Тольяттинского государственного университета. 2014. № 1 (27). С. 127-129.
4. Семененко М.Г., Кулакова Н.Н. Прогнозирование финансовой устойчивости предприятия на основе формализма нечеткой логики // Международный журнал прикладных и фундаментальных исследований. 2014. № 5-2. С. 191-192.
5. http://www.scilab.org

Все статьи автора «Семененко Марина Геннадиевна»